
所属成套资源:2023年高考数学二轮复习重点基础练习
2023年高考数学二轮复习重点基础练习:专题二 考点04 函数及其表示(C卷)
展开
这是一份2023年高考数学二轮复习重点基础练习:专题二 考点04 函数及其表示(C卷),共7页。试卷主要包含了函数的定义域为,若,则,下列两数中,不满足的是,如图所示的四个容器高度都相同,已知函数则的值为,设函数则的取值范围为等内容,欢迎下载使用。
专题二 考点04 函数及其表示(C卷) 1.函数的定义域为( )A. B.C. D.2.若,则( )A.1 B. C.0 D.-13.下列两数中,不满足的是( )
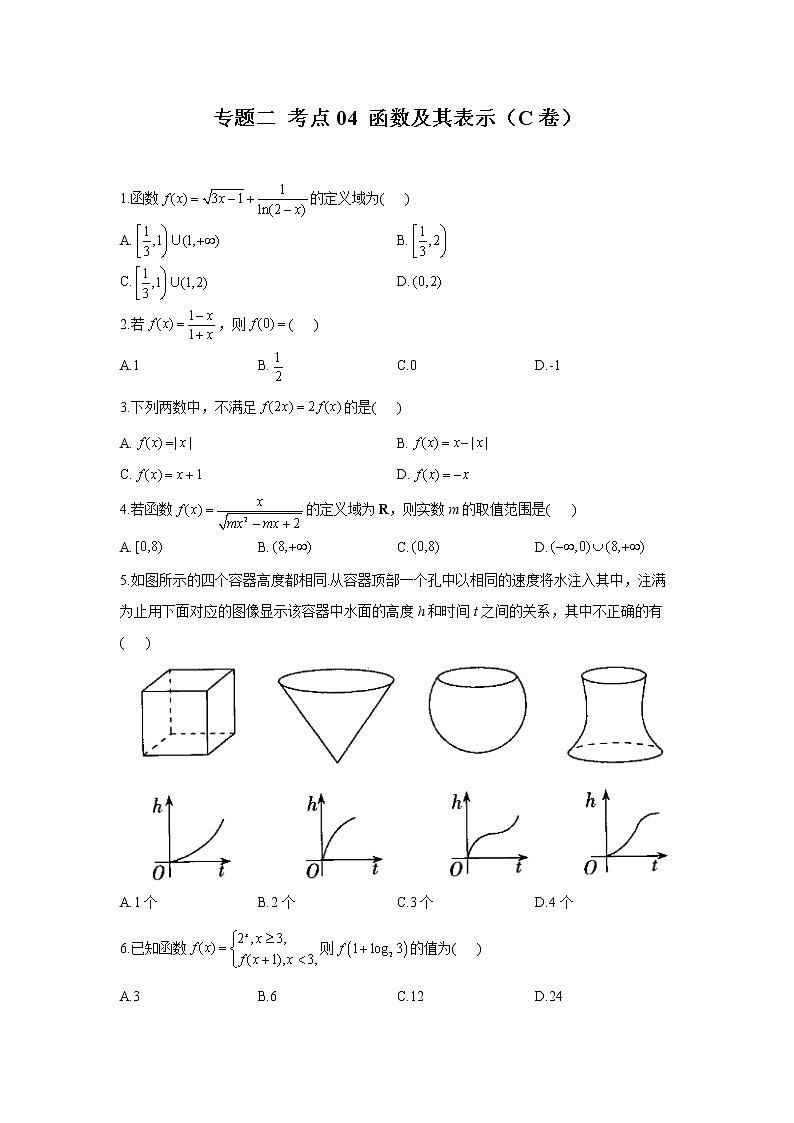
A. B.C. D.4.若函数的定义域为R,则实数m的取值范围是( )A. B. C. D.5.如图所示的四个容器高度都相同.从容器顶部一个孔中以相同的速度将水注入其中,注满为止用下面对应的图像显示该容器中水面的高度h和时间t之间的关系,其中不正确的有( )
A.1个 B.2个 C.3个 D.4个6.已知函数则的值为( )A.3 B.6 C.12 D.247.若函数的定义域为,值域为,则实数m的取值范围是( )
A. B. C. D.8.设函数则的取值范围为( )A. B.C. D.9.某位喜欢思考的同学在学习函数的性质时提出了如下两个命题:已知函数的定义域为.①若对,都有,则函数是上的奇函数;②若对,都有,则函数是上的奇函数.下列判断正确的是( )A.①和②都是真命题B.①是真命题,②是假命题C.①和②都是假命题D.①是假命题,②是真命题10.已知函数若,则实数m的取值范围为( )A. B.C. D.11.若函数,,则_____________.12.已知函数的定义域为,则函数的定义域是__________.13.若集合,,其中,,,,是从定义域A到值域B的一个函数,则____________.14.已知函数,由下表给出:x123131321则满足不等式的解集是___________.15.已知且,若函数的值域为,则实数a的取值范围是____________.
答案以及解析1.答案:C解析:要使函数有意义,则故函数的定义域为.故选C.2.答案:A解析:,.故选A.3.答案:C解析:若,则,,,即不满足,故选C.4.答案:A解析:函数的定义域为R,不等式的解集为R.①当时,恒成立,满足题意;②当时,则解得.综上可得,实数m的取值范围是.故选A.5.答案:A解析:对于第一个容器,水面的高度h的增加应是匀速的,因此不正确,其他均正确,故选A.6.答案:C解析:函数且,,.故选C.7.答案:C解析:如图,作出函数的图像.由图可知,,故选C.
8.答案:B解析:作出的图象如图中实线所示,由图可知,设,则,因为,所以,,所以或因为在上单调递减,所以,所以的取值范围为,故选B.9.答案:B解析:函数的定义域为.①若对,都有,可得关于原点对称,由奇函数的定义可得函数是上的奇函数,故①是真命题;②若对,都有,则函数是上的增函数,奇偶性不确定.故选B.10.答案:D解析:当时,,所以,即,解得.当时,,所以,即,解得.综上,实数m的取值范围为,故选D.11.答案:4038解析:.12.答案:解析:由题意知即从而,故函数的定义域为.13.答案:7解析:,,,,,,,,.当时,,不满足,当时,或(舍去),故.因此,,从而,故答案为7.14.答案:解析:若,则,,此时不成立;
若,则,,此时成立;
若,则,,此时不成立.故不等式的解集为.15.答案:解析:因为函数的值域为,且,,当时,,所以可得.
相关试卷
这是一份2023届高考数学二轮复习专题二函数及其表示(C卷)含答案,共8页。试卷主要包含了已知函数,则,已知函数,若,则,已知函数满足,则,定义等内容,欢迎下载使用。
这是一份2023年高考数学二轮复习重点基础练习:专题四 考点11 函数与方程(C卷),共10页。试卷主要包含了已知函数则函数的零点个数为等内容,欢迎下载使用。
这是一份2023年高考数学二轮复习重点基础练习:专题二 考点05 函数的单调性与最值(C卷),共7页。试卷主要包含了函数的单调递减区间为,函数的图象如图所示,则,函数的最大值为,已知函数的定义域为,若满足等内容,欢迎下载使用。









