2023年高考数学二轮复习重点基础练习：专题六 考点16 三角函数的图象及其变换（A卷）

这是一份2023年高考数学二轮复习重点基础练习：专题六 考点16 三角函数的图象及其变换（A卷），共10页。试卷主要包含了函数在区间上的简图是，函数，的大致图象为，已知函数的图像如图所示，，则等内容，欢迎下载使用。
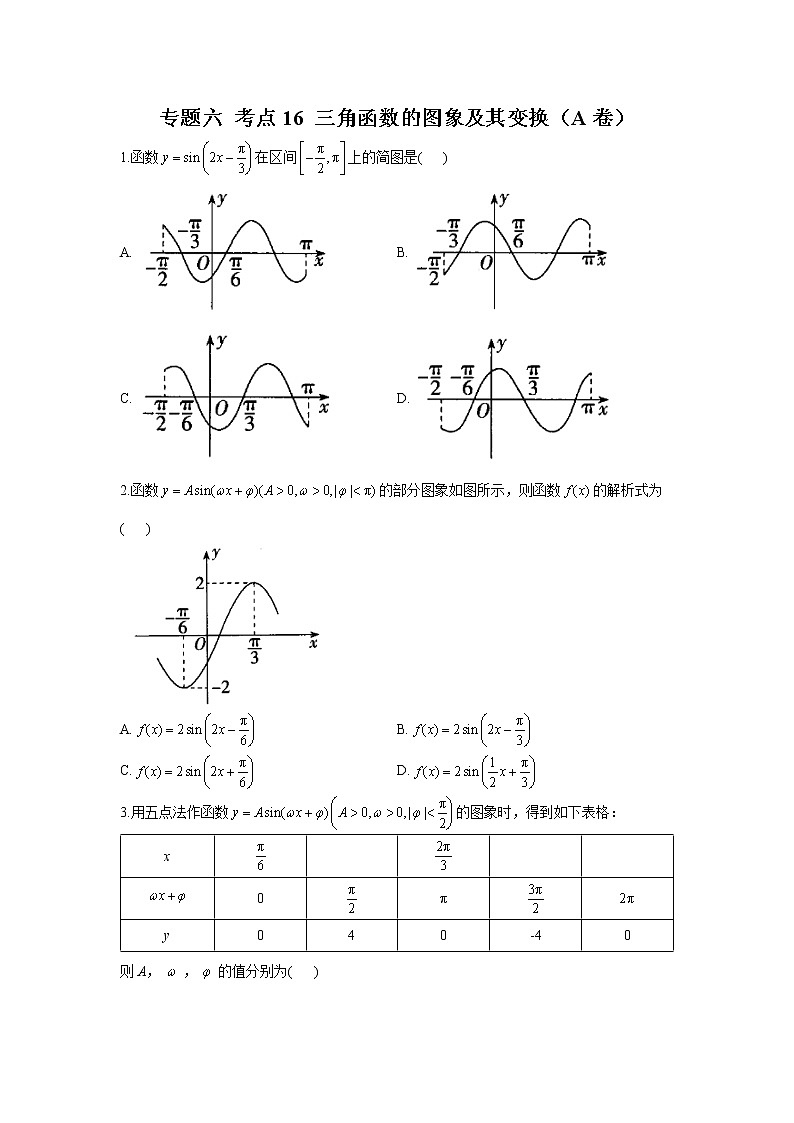
专题六 考点16 三角函数的图象及其变换（A卷）1.函数在区间上的简图是(   )A. B.C. D.2.函数的部分图象如图所示，则函数的解析式为(   )A.  B.C.  D.3.用五点法作函数的图象时，得到如下表格：x   0πy040-40则A，，的值分别为(   )A.4，2， B.4，， C.4，2， D.4，，4.函数，的大致图象为(   )
A. B.
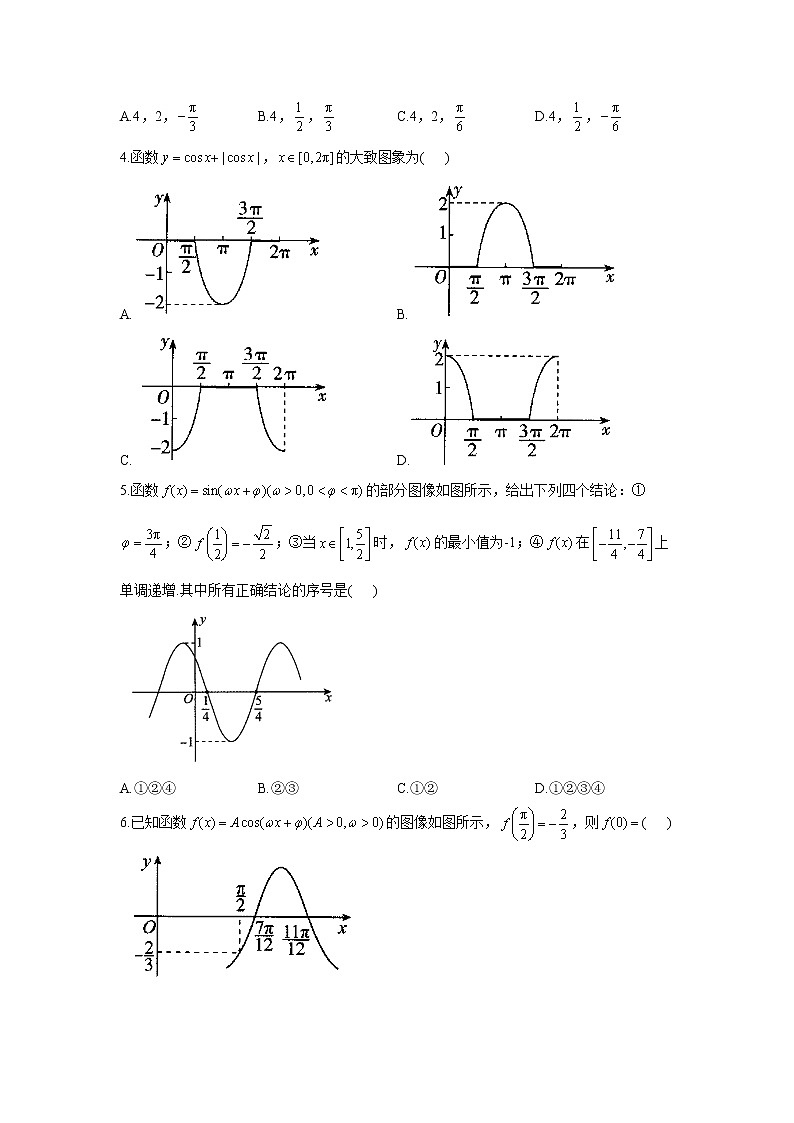
C. D.5.函数的部分图像如图所示，给出下列四个结论：①；②；③当时，的最小值为-1；④在上单调递增.其中所有正确结论的序号是(   )
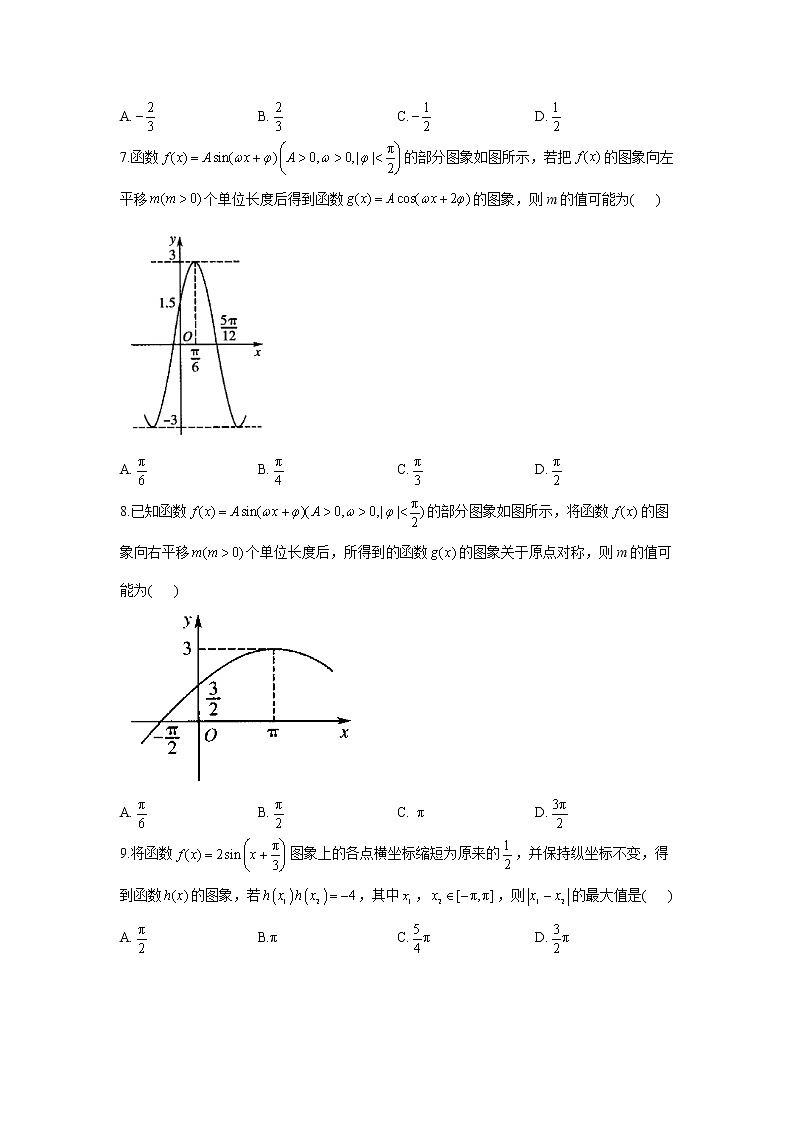
 A.①②④ B.②③ C.①② D.①②③④6.已知函数的图像如图所示，，则(   )A. B. C. D.7.函数的部分图象如图所示，若把的图象向左平移个单位长度后得到函数的图象，则m的值可能为(   )A. B. C. D.8.已知函数的部分图象如图所示，将函数的图象向右平移个单位长度后，所得到的函数的图象关于原点对称，则m的值可能为(   )A. B. C. D.9.将函数图象上的各点横坐标缩短为原来的，并保持纵坐标不变，得到函数的图象，若，其中，，则的最大值是(   )A. B.π C. D.10.已知函数的最小正周期为π，将函数的图象沿x轴向右平移个单位长度，得到函数的图象，则下列说法正确的是(   )A.函数在上是增函数B.函数的图象关于直线对称C.函数是奇函数D.函数的图象关于点中心对称11.函数的定义域为，值域为，则的最大值与最小值之和等于__________.12.已知函数的部分图象如图所示，则的值为_________.13.将函数的图象向右平移个单位长度后，与函数的图象重合，则_________.14.已知函数的部分图象如图所示，则__________.15.已知函数.（1）求的最小正周期；（2）若函数的图象是由的图象向右平移个单位长度，再向上平移1个单位长度得到的，当时，求的最大值和最小值.
答案以及解析1.答案：A解析：当时，，故可排除B、D；当时，，排除C.故选A.2.答案：A解析：由题图可得，，，由五点作图法，可得，，故，故选A.3.答案：A解析：由题表中y的最大值为4，最小值为-4，可得，由，得，，，其图象过点，，，得，，当时，.故选A.4.答案：D解析：由题意得易知D中图象符合要求，故选D.5.答案：C解析：由图可知，所以，所以，所以因为函数图像过点，所以，即，得，又，所以，所以，所以，故①②正确；当时，，此时，故③错误；
当时，，因为在上不单调，故在上不单调，故④错误，故选C.6.答案：B解析：由题图可知，所求函数的最小正周期，故.将代入解析式，得，即.令，代入解析式得.又，，.7.答案：C解析：由题意可知：，.且，，.把函数的图象向左平移m个单位长度得的图象，，.当时，，故选C.8.答案：B解析：由题意得，，.又，.将的图象向右平移个单位长度后得到的函数解析式为.由题意可知，函数为奇函数，，，当时，，故选B.9.答案：D解析：解法一  由题意可知，所以，因为，所以或当时，，即，，即，因为，，所以或，或，所以当，时，取得最大值，最大值是.同理，当时，的最大值也是.故选D.解法二  由题意可知，所以，因为，所以或因为函数的最小正周期，当时，有两个周期，即出现两次最大值和最小值，所以的最大值为.故选D.10.答案：A解析：，，得，因此，，对于A，由，得，此时单调递减，则函数单调递增，故A正确；对于B，令，，得，，故B错误；对于C，，则函数是偶函数，故C错误；对于D，令，，得，，当时，，故D错误.故选A.11.答案：解析：如图所示，当时值域为，且取得最大值.当时，值域为，且取得最小值.的最大值与最小值之和为.
 12.答案：解析：由题图可得，，或，由于在函数的单调递减区间内，所以取，故答案为.13.答案：解析：将函数的图象向右平移个单位长度后得到的图象，.由题意可知，.又.14.答案：解析：由题图可知，所以，因此，所以，又函数图象过点，所以，即，，解得，，又因为，所以.故答案为.15.答案：（1），所以函数的最小正周期为.（2）依题意得，因为，所以.当，即时，取最大值，为；当，即时，取最小值，为0.