2023年高考数学二轮复习重点基础练习：专题七 考点19 正、余弦定理及解三角形（A卷）

这是一份2023年高考数学二轮复习重点基础练习：专题七 考点19 正、余弦定理及解三角形（A卷），共8页。试卷主要包含了考点19等内容，欢迎下载使用。
 专题七 考点19 正、余弦定理及解三角形（A卷）1.在中，内角A，B，C所对的边分别是a，b，c.若，，则(   )A. B. C. D.22.在锐角三角形ABC中，a，b，c分别是内角A，B，C的对边.若，则的取值范围是(   )A. B. C. D.3.在中，（a，b，c分别为内角A，B，C的对边），则的形状为(   )A.等边三角形  B.直角三角形C.等腰三角形或直角三角形 D.等腰直角三角形4.在中，内角A，B，C所对的边分别是a，b，c.若，，则的面积是(   )A.3 B. C. D.5.如图，一艘船自西向东匀速航行，上年10时到达一座灯塔P的南偏西75°、距塔68海里的M处，下午2时到达这座灯塔的东南方向的N处，则这艘船航行的速度为(   )A.海里/时  B.海里/时C.海里/时  D.海里/时6.在中，a，b，c分别为内角A，B，C的对边.如果，，的面积为，那么(   )A. B. C. D.7.在中，内角A，B，C所对的边分别为a，b，c，已知，，，则(   )A. B. C. D.8.在中，内角A，B，C的对边分别为a，b，c，若，则的外接圆的面积为(   )
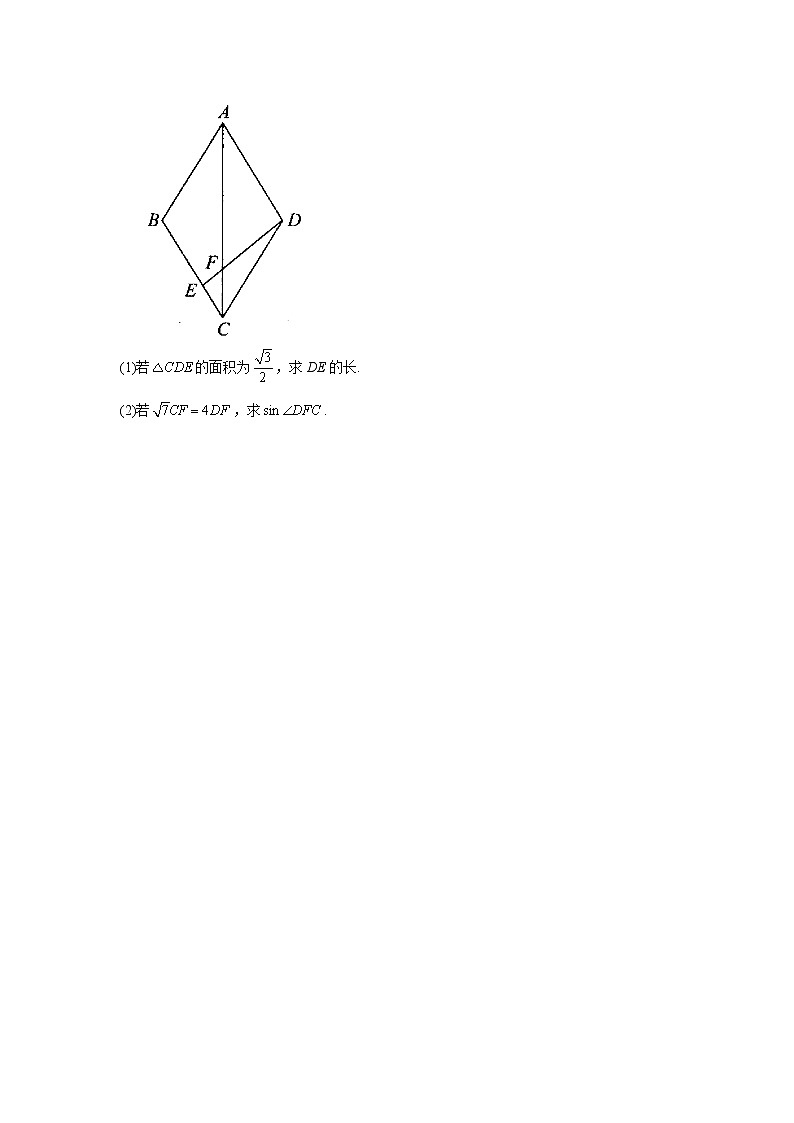
A. B. C. D.9.在中，内角A，B，C的对边分别为a，b，c，其中，，的面积为，则的最小值为(   )A. B. C. D.10.在中，若，则___________.11.在中，角A，B，C的对边分别为a，b，c，若，则______.12.已知中，的对边分别为，若，则周长的取值范围是_____________.13.某人在M汽车站的北偏西20°的方向上的A处，观察到点C处有一辆汽车沿公路向M站行驶.公路的走向是M站的北偏东40°.开始时，汽车到A的距离为31千米，汽车前进20千米后，到A的距离缩短了10千米.则汽车到达M汽车站还需行驶_________km.14.在中，点D在BC边上，.(1)求的值；(2)若，求AD的长.15.已知菱形ABCD的边长为2，，E是边BC上一点，线段DE交AC于点F.(1)若的面积为，求DE的长.(2)若，求.
答案以及解析1.答案：D解析：在中，由正弦定理得，，.故选D.2.答案：C解析：，.由正弦定理得.，，，，.故选C.3.答案：B解析：，，，即，整理得，为直角三角形.故选B.4.答案：B解析：由可得，又由余弦定理得，所以，解得.则.故选B.5.答案：A解析：由题意得在中，，，，.由正弦定理得，，解得，则这般船航行的速度为（海里/时）.故选A.6.答案：B解析：由，得.由余弦定理，得，所以.7.答案：A解析：由题知，，由余弦定理得，.由正弦定理，得.故选A.8.答案：B解析：在中，，所以.设的外接圆的半径为R，则由正弦定理，可得，解得，故的外接圆的面积，故选B.9.答案：C解析：因为，所以，所以.又因为，所以，所以，所以，当且仅当，即，或，时，等号成立，故的最小值为.故选C.10.答案：解析：由正弦定理得：，所以.又，所以，所以，所以.11.答案：4解析：由余弦定理得，因为，所以，整理得，解得(舍去)或.12.答案：解析：在中，由余弦定理可得，化简可得.，解得(当且仅当时，取等号).故.再由任意两边之和大于第三边可得，故有，所以的周长的取值范围是.13.答案：15解析：由题意，画出北示意图，设汽车前进20千米后到达B处.在中，，由余弦定理，得，则，所以.在中，由正弦定理，得.从而有.故汽车到达M汽车站还需行驶15km.14.答案：(1).(2).解析：(1)因为，且，所以，由得，又因为，所以.(2)在中，由，得.15.答案：(1)(2)解析：(1)依题意，得.因为的面积，所以，解得.在中，由余弦定理得.(2)方法一：连接BD.依题意，得，设，则，在中，由正弦定理得，因为，所以，所以，所以.方法二：连接BD.依题意，得，，设，则，设，因为，则，在中，由余弦定理，得，即，解得，或.又因为，所以，所以，所以，在中，由正弦定理得，所以.