2023年高考数学二轮复习重点基础练习：专题十一 考点31 空间几何体（A卷）

这是一份2023年高考数学二轮复习重点基础练习：专题十一 考点31 空间几何体（A卷），共9页。试卷主要包含了下列说法正确的是，2008年北京奥运会游泳中心，已知四面体中，，且等内容，欢迎下载使用。
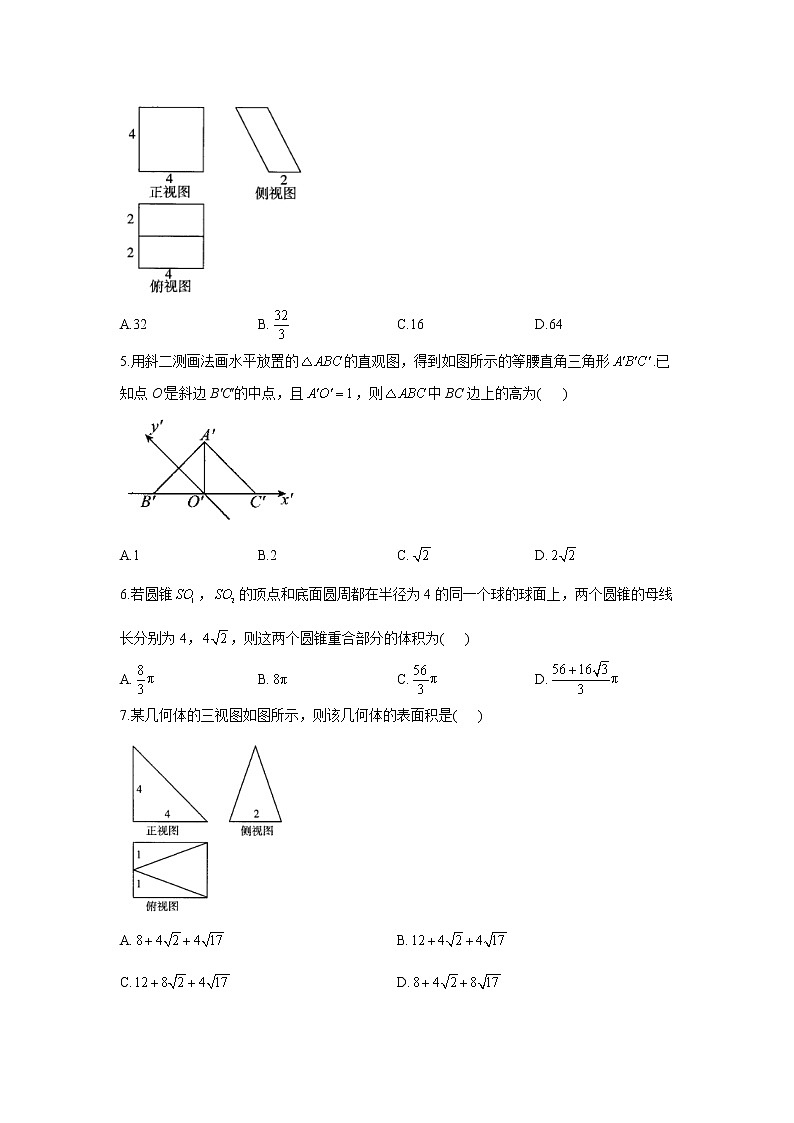
专题十一 考点31 空间几何体（A卷）1.下列说法正确的是(   )A.圆锥的底面是圆面，侧面是曲面B.用一张扇形的纸片可以卷成一个圆锥C.一个物体上、下两个面是相等的圆面，那么它一定是一个圆柱D.圆台的任意两条母线的延长线可能相交也可能不相交2.如图所示，观察四个几何体，其中判断正确的是(   )A.是棱台 B.是圆台C.不是棱柱 D.是棱锥3.如图所示的几何体，关于其结构特征，下列说法不正确的是(   )A.该几何体是由2个同底的四棱锥组成的几何体B.该几何体有12条棱、6个顶点C.该几何体有8个面，并且各面均为三角形D.该几何体有9个面，其中一个面是四边形，其余各面均为三角形4.已知某几何体的三视图如图所示，则该几何体的体积为(   )A.32 B. C.16 D.645.用斜二测画法画水平放置的的直观图，得到如图所示的等腰直角三角形.已知点O'是斜边B'C'的中点，且，则中BC边上的高为(   )A.1 B.2 C. D.6.若圆锥，的顶点和底面圆周都在半径为4的同一个球的球面上，两个圆锥的母线长分别为4，，则这两个圆锥重合部分的体积为(   )A. B. C. D.7.某几何体的三视图如图所示，则该几何体的表面积是(   )A.  B.C.  D.8.2008年北京奥运会游泳中心（水立方）的设计灵感源自威尔—弗兰泡沫，威尔—弗兰泡沫是对开尔文胞体的改进.开尔文胞体是一种多面体，它由正六边形和正方形围成（其中每一个顶点处有一个正方形和两个正六边形）.已知该多面体共有24个顶点，且棱长为1，则该多面体的表面积是(   )A. B. C. D.9.表面积为的球面上有三点A，B，C，.作平面ABC，平面ABC，平面ABC，交球面于，则多面体的体积最大值为(   )A. B. C. D.10.已知四面体中，，且.若四面体的外接球体积为，则当该四面体的体积最大时，(   )A.2 B.4 C.6 D.811.给出下列说法：①圆柱的底面是圆面；②经过圆柱任意两条母线的截面是一个矩形面；③圆台的任意两条母线的延长线可能相交，也可能不相交；④夹在圆柱的两个截面间的几何体还是一个旋转体.其中说法正确的是________.(填序号)12.如图所示的直观图，其平面图形的面积为_______.13.已知某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的体积为__________，表面积为__________.14.已知四棱台的上、下底面分别是边长为4和8的正方形，侧面是腰长为8的等腰梯形，则该四棱台的表面积为__________.15.已知圆柱的底面圆O的半径为4，矩形为圆柱的轴截面，C为圆O上一点，，圆柱的表面积为，则三棱锥的体积与其外接球的体积之比为____________.
答案以及解析1.答案：A解析：A是圆锥的性质，故正确；对于B，动手操作一下，发现一张扇形的纸片只能卷成一个无底面的圆锥，故B错误；对于C，根据圆柱的结构特征可知，若两个相等的圆面不平行，那么这个物体不是圆柱，故C错误；对于D，圆台是由圆锥截得的，故其任意两条母线延长后一定交于一点，故D错误.2.答案：D解析：对于A选项，侧棱延长线不交于一点，不符合棱台的定义，A错误；对于B选项，上、下两个面不平行，不符合圆台的定义，B错误；对于C选项，将几何体竖直起来看，符合棱柱的定义，C错误；对于D选项，符合棱锥的定义，D正确.故选D.3.答案：D解析：该几何体用平面ABCD可分割成两个四棱锥，因此它是这两个四棱锥的组合体，因而四边形ABCD是它的一个截面而不是一个面，故D说法不正确.4.答案：A解析：由三视图可知该几何体为一个横放的直四棱柱，其中直四棱柱的底面是平行四边形(边长为2的边上的高为4)，高为4，则该几何体的体积，故选A.5.答案：D解析：直观图是等腰直角三角形，，，.根据直观图中平行于y轴的长度变为原来的一半，的BC边上的高.故选D.6.答案：A解析：如图，因为球的半径，圆锥的母线长，圆锥的母线长，易知，，.记SB与圆锥的底面交于A点，则C，A，三点共线，且，则两圆锥重合部分的体积.故选A.7.答案：B解析：由三视图可知，该几何体是一个底面为矩形(长为4、宽为2)，高为4的四棱锥，其中一个侧面与底面垂直，所以该几何体的表面积，故选B.8.答案：C解析：本题考查多面体表面积的求解.边长为1的正方形的面积为，正六边形的面积为.因为每一个顶点处有一个正方形和两个正六边形，该多面体有24个顶点，所以该多面体中正方形有（个），正六边形有（个），所以该多面体的表面积为，故选C.9.答案：C解析：，由正弦定理可得的外接圆的直径为.又球的表面积为，设球的半径为R，则，所以球的半径为.设球心为O，球心O到截面ABC的距离为d，由球的截面性质，可得(r为截面圆半径)，则球心到平面ABC的距离d为2.由已知条件可得几何体为三棱柱，由球的对称性可得三棱柱的高为4.在三角形ABC中由余弦定理可得，再由基本不等式可得，当且仅当时取等号，所以的面积的最大值为，由此可得多面体的体的最大值为，故选C.10.答案：B解析：如图，由，得，，，又，平面PAB，则，又，平面ABC.取PC中点O，可得，则O为四面体的外接球的球心，设外接球的半径为R，由外接球体积为，得，即..又，设，，则，即..当且仅当时上式取等号.故选：B.11.答案：①②解析：①正确，圆柱的底面是圆面；②正确，如图所示，经过圆柱任意两条母线的截面是一个矩形面；③不正确，圆台的母线延长，相交于一点；④不正确，夹在圆柱两个平行于底面的截面间的几何体才是旋转体.12.答案：6解析：由直观图可知其对应的平面图形AOB中，，所以.13.答案：；解析：由三视图可知，该几何体是一个半圆柱与一个三棱柱的组合体，所以该几何体的体积为，表面积为.14.答案：解析：如图，在四棱台中，过作，垂足为F，在中，，故，所以，故四棱台的侧面积，所以.15.答案：解析：如图所示，由题意知圆柱的表面积，故.在中，，所以，所以，所以，.由题意知平面，所以，结合，得平面，所以.取的中点，则由与为直角三角形知，为三棱锥外接球的球心，球的半径，所以外接球的体积，所以.