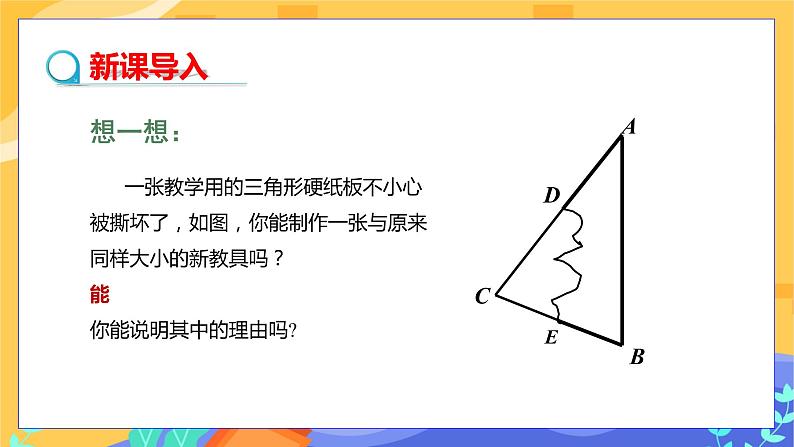
数学七年级下册3 探索三角形全等的条件完美版课件ppt

教学目标

1.掌握用“角边角”和“角角边”证明两个三角形全等的方法．

2.由探索三角形“两角一边”全等条件的过程，体会由操作、归纳获得数学结论的过程．

教学重难点

重点: 会用“角边角”和“角角边”证明两个三角形全等．

难点：1.能运用“角边角”“角角边”判定方法解决有关问题；2.体会由操作、归纳获得数学结论的过程．

教学过程

导入新课

 如图所示，某同学把一块三角形的玻璃不小心打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是带哪块去？（学生先独立思考，然后再与同学进行交流）

【老师点评】仅仅带①或②是无法配成完全一样的玻璃的，而仅仅带③则可以，为什么呢？本节课我们继续研究三角形全等的判定方法．

探究新知

一、预习新知

阅读教材P100～P101的内容，回答下列问题.

1．两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．

通常写成下面的格式：

在△ABC与△DEF中，

所以△ABC≌△DEF.

2．两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”．

通常写成下面的格式：

在△ABC与△DEF中，

所以△ABC≌△DEF.

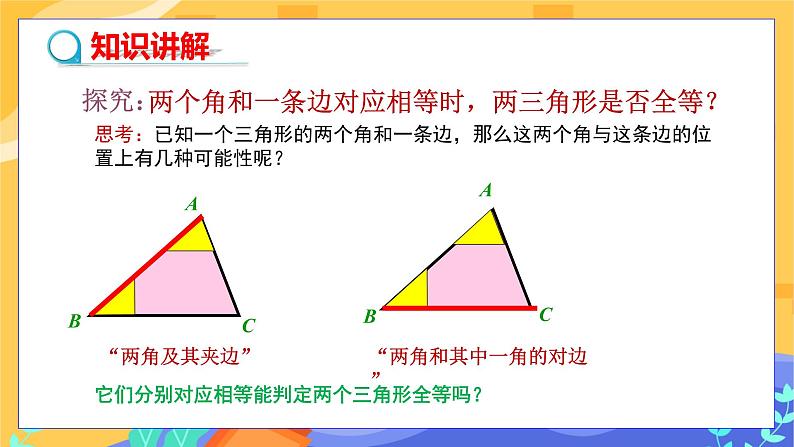
二、合作探究

【问题】如果已知一个三角形的两角及一边，那么有几种可能的情况呢？每种情况下得到的三角形都全等吗？

两种情况：两角及其夹边，两角和其中一角的对边.

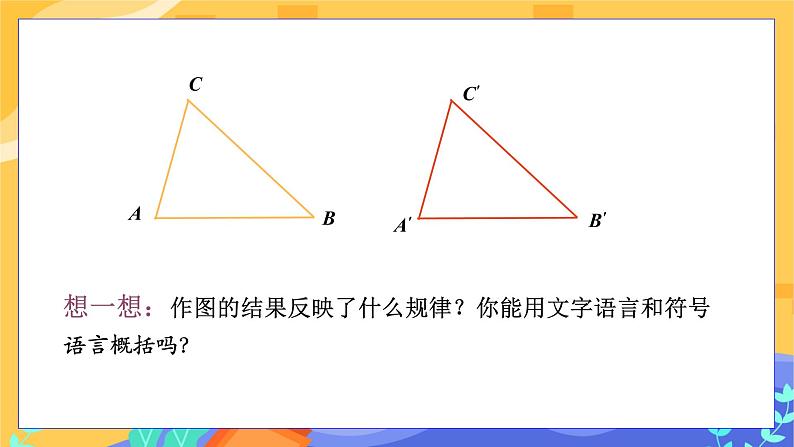
探究1：两角及其夹边对应相等时，两三角形是否全等？

【操作】先任意画出一个△ABC，再画一个△A′B′C′， 使A′B′＝AB，

∠A′＝∠A， ∠B′＝∠B (即使两角和它们的夹边对应相等).

把画好的△A′B′C′剪下来，放到△ABC上，它们全等吗？

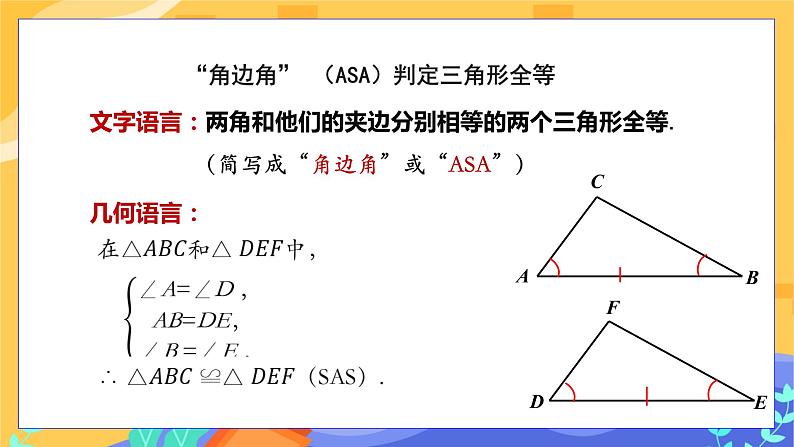
发现：两个三角形完全重合，是全等的.

【结论】

两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．

【问题】

此判定方法用符号语言怎么表示？

在△ABC与△DEF中，

所以△ABC≌△DEF.

例  如图，已知AD∥BC，BE∥DF，AE＝CF，求证：△ADF ≌△CBE.

【问题探索】回忆学过的判定三角形全等的条件，结合已知中的平行线段，可考虑利用“ASA”证明△ADF≌△CBE.

【证明】因为AD∥BC，BE∥DF，

所以∠A＝∠C，∠DFA＝∠BEC．

因为AE＝CF，

所以AE＋EF＝CF＋EF，即AF＝CE.

在△ADF和△CBE中，

所以△ADF≌△CBE(ASA)．

探究2：两角和其中一角的对边对应相等时，两三角形是否全等？

【思考】如图，在△ABC和△DEF中， ∠A=∠D， ∠B=∠E ，BC=EF，

△ABC与△DEF全等吗？能利用角边角条件证明你的结论吗？

已知∠A=∠D， ∠B=∠E ，由三角形内角和定理可得∠C=∠F. 之后可利用ASA证明全等.

发现：两个三角形是全等的.

【结论】

两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”．

【问题】

此判定方法用符号语言怎么表示？

在△ABC与△DEF中，

所以△ABC≌△DEF.

课堂小结

1.两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．

2.两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”．

布置作业

完成教材习题4.7

板书设计

利用“角边角”“角角边”判定三角形全等

两角及其夹边分别相等的两个三角形全等，简写成“角边角”或“ASA”．

两角分别相等且其中一组等角的对边相等的两个三角形全等，简写成“角角边”或“AAS”．