初中数学北师大版八年级下册2 直角三角形教学设计及反思

这是一份初中数学北师大版八年级下册2 直角三角形教学设计及反思，共5页。教案主要包含了课堂引入，探究新知，典型例题，变式训练，课堂检测等内容，欢迎下载使用。
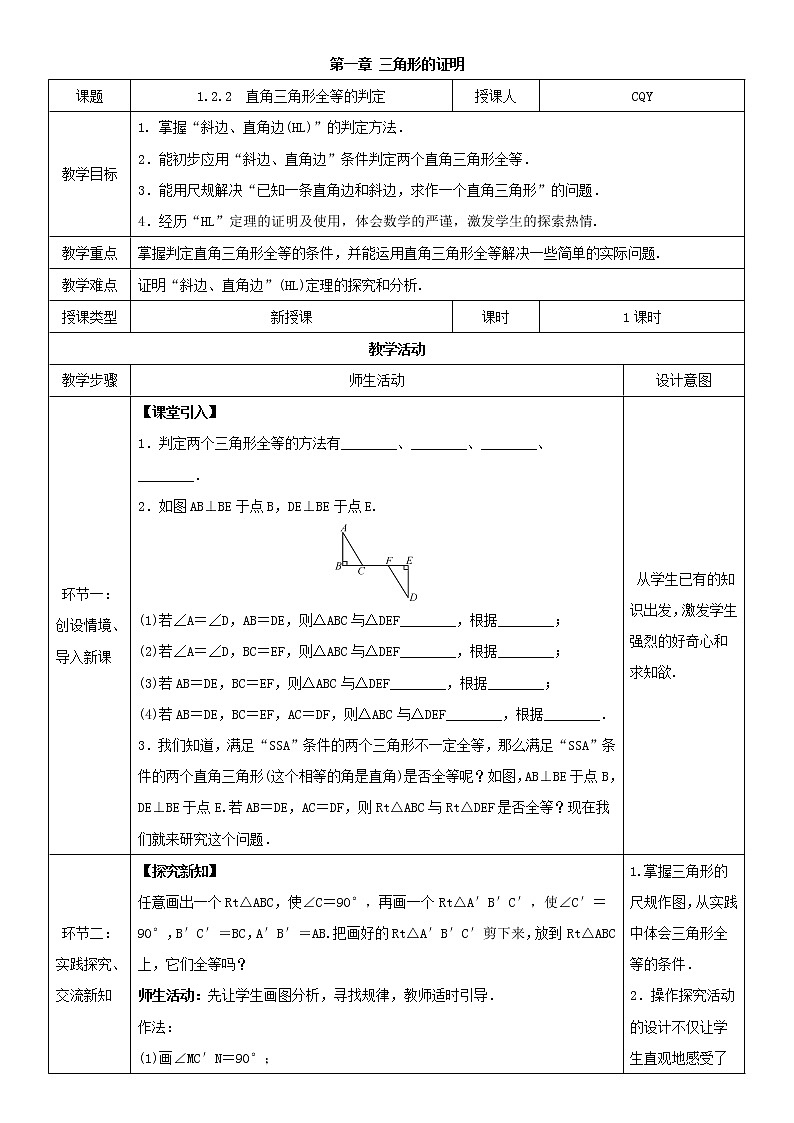
第一章    三角形的证明课题1.2.2　直角三角形全等的判定授课人CQY教学目标 掌握“斜边、直角边(HL)”的判定方法．2．能初步应用“斜边、直角边”条件判定两个直角三角形全等．3．能用尺规解决“已知一条直角边和斜边，求作一个直角三角形”的问题．4．经历“HL”定理的证明及使用，体会数学的严谨，激发学生的探索热情.教学重点掌握判定直角三角形全等的条件，并能运用直角三角形全等解决一些简单的实际问题.教学难点证明“斜边、直角边”(HL)定理的探究和分析.授课类型新授课课时1课时教学活动教学步骤师生活动设计意图环节一：创设情境、导入新课【课堂引入】1．判定两个三角形全等的方法有________、________、________、________．2．如图AB⊥BE于点B，DE⊥BE于点E.(1)若∠A＝∠D，AB＝DE，则△ABC与△DEF________，根据________； (2)若∠A＝∠D，BC＝EF，则△ABC与△DEF________，根据________； (3)若AB＝DE，BC＝EF，则△ABC与△DEF________，根据________； (4)若AB＝DE，BC＝EF，AC＝DF，则△ABC与△DEF________，根据________．3．我们知道，满足“SSA”条件的两个三角形不一定全等，那么满足“SSA”条件的两个直角三角形(这个相等的角是直角)是否全等呢？如图，AB⊥BE于点B，DE⊥BE于点E.若AB＝DE，AC＝DF，则Rt△ABC与Rt△DEF是否全等？现在我们就来研究这个问题． 从学生已有的知识出发，激发学生强烈的好奇心和求知欲.环节二：实践探究、交流新知【探究新知】任意画出一个Rt△ABC，使∠C＝90°，再画一个Rt△A′B′C′，使∠C′＝90°，B′C′＝BC，A′B′＝AB.把画好的Rt△A′B′C′剪下来，放到Rt△ABC上，它们全等吗？师生活动：先让学生画图分析，寻找规律，教师适时引导．作法： (1)画∠MC′N＝90°；(2)在射线C′M上截取B′C′＝BC；(3)以点B′为圆心，AB为半径画弧，交射线C′N于点A′；(4)连接A′B′.则△A′B′C′即为所求作的三角形(如图)．【猜想】 斜边和一条直角边分别相等的两个直角三角形全等【证明】 斜边和一条直角边分别相等的两个直角三角形全等(简写成“斜边、直角边”或“HL”)．1．分析命题：条件：两个直角三角形的斜边和一条直角边分别相等；结论：这两个直角三角形全等．2．数学语言：已知：如图，在△ABC和△A′B′C′中，∠C＝∠C′＝90°，AC＝A′C′，AB＝A′B′；求证：△ABC≌△A′B′C′.证明：在△ABC中，∵∠C＝90°，∴BC2＝AB2－AC2(勾股定理)．同理，B′C′2＝A′B′2－A′C′2.∵AB＝A′B′，AC＝A′C′，∴BC＝B′C′.∴△ABC≌△A′B′C′(SSS)．定理：斜边和一条直角边分别相等的两个直角三角形全等(HL)．符号表示：在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，∵AC＝A′C′，AB＝A′B′(已知)，∴Rt△ABC≌Rt△A′B′C′(HL).1.掌握三角形的尺规作图，从实践中体会三角形全等的条件．2．操作探究活动的设计不仅让学生直观地感受了“斜边、直角边”可以确定一个直角三角形的大小和形状，而且也让学生较好地感悟到“斜边、直角边”可以判定两个直角三角形全等．3．培养学生的识图能力，并规范证明过程的书写格式.环节三：开放训练、体现应用【典型例题】例1　如图，有两个长度相同的滑梯，左边滑梯的高度AC与右边滑梯水平方向的长度DF相等，两个滑梯的倾斜角∠ABC和∠EFD的大小有什么关系？解：根据题意，可知∠BAC＝∠EDF＝90°，BC＝EF，AC＝DF，∴Rt△ABC≌Rt△DEF(HL)．∴∠ABC＝∠DEF.∵∠DEF＋∠EFD＝90°，∴∠ABC＋∠EFD＝90°.例2　如图，∠BAC＝90°，AD是∠BAC内部一条射线，若AB＝AC，BE⊥AD于点E，CF⊥AD于点F.求证：AF＝BE.证明：∵∠BAC＝90°，∴∠BAE＋∠FAC＝90°.∵BE⊥AD，CF⊥AD，∴∠BEA＝∠AFC＝90°.∴∠BAE＋∠EBA＝90°.∴∠EBA＝∠FAC.在△ACF和△BAE中，∴△ACF≌△BAE(AAS)∴AF＝BE.【变式训练】1．如图，在△ABC中，D是边BC上的点，DE⊥AC，DF⊥AB，垂足分别为E，F，且DE＝DF，CE＝BF.求证：∠B＝∠C.证明：∵DE⊥AC，DF⊥AB，∴∠BFD＝∠CED＝90°.在△BDF和△CDE中，∴△BDF≌△CDE(SAS)．∴∠B＝∠C.2．如图，在四边形ABCD中，∠ABC＝∠ADC＝90°，BE⊥AC于点E，DF⊥AC于点F，CF＝AE，BC＝DA.求证：Rt△ABE≌Rt△CDF.解：在Rt△ADC和Rt△CBA中，∴Rt△ADC≌Rt△CBA(HL)．∴DC＝BA.又∵BE⊥AC，DF⊥AC，∴∠AEB＝∠CFD＝90°.在Rt△ABE和Rt△CDF中，∴Rt△ABE≌Rt△CDF(HL)．1.培养学生逻辑思维能力，学会用“HL”条件判定三角形全等．2．规范使用“HL”判定方法证明三角形全等的书写格式．在证明两个直角三角形全等时，要防止学生使用“SSA”来证明.环节四：课堂检测、巩固新知【课堂检测】1.下列各选项中的两个直角三角形不一定全等的是(B)A．两条直角边对应相等的两个直角三角形B．两个锐角对应相等的两个直角三角形C．斜边和一条直角边对应相等的两个直角三角形D．有一个锐角及这个锐角的对边对应相等的两个直角三角形2．如图，PB⊥AB于点B，PC⊥AC于点C，且PB＝PC，D是AP上一点．求证：∠BDP＝∠CDP.证明：∵PB⊥AB于点B，PC⊥AC于点C，∴∠ABP＝∠ACP＝90°.∵PB＝PC，AP＝AP，∴Rt△ABP≌Rt△ACP(HL)．∴∠APB＝∠APC.在△PBD和△PCD中，∴△PBD≌△PCD(SAS)．∴∠BDP＝∠CDP.了解学生对本节课知识的掌握程度、理解程度和运用程度．运用直角三角形的判定方法解决实际问题，提高学生解决问题的能力.环节五：课堂小结、整体感知1.课堂小结：本节课学到了什么知识？（1）定理：斜边和一条直角边分别相等的两个直角三角形全等(HL)．（2）符号表示：在Rt△ABC和Rt△A′B′C′中，∠C＝∠C′＝90°，∵AC＝A′C′，AB＝A′B′(已知)，∴Rt△ABC≌Rt△A′B′C′(HL).2．布置作业：(1)教材第20页随堂练习第1，2题．(2)教材第21页习题1.6第1，2，3题.小结环节的设置能够让学生养成自主归纳课堂重点的习惯，提高学生的学习能力.板书设计 教学反思