2022-2023学年山西省朔州市怀仁县第九中学高一上学期第一次月考数学试题（解析版）

这是一份2022-2023学年山西省朔州市怀仁县第九中学高一上学期第一次月考数学试题（解析版），共15页。试卷主要包含了单选题，多选题，填空题，解答题等内容，欢迎下载使用。
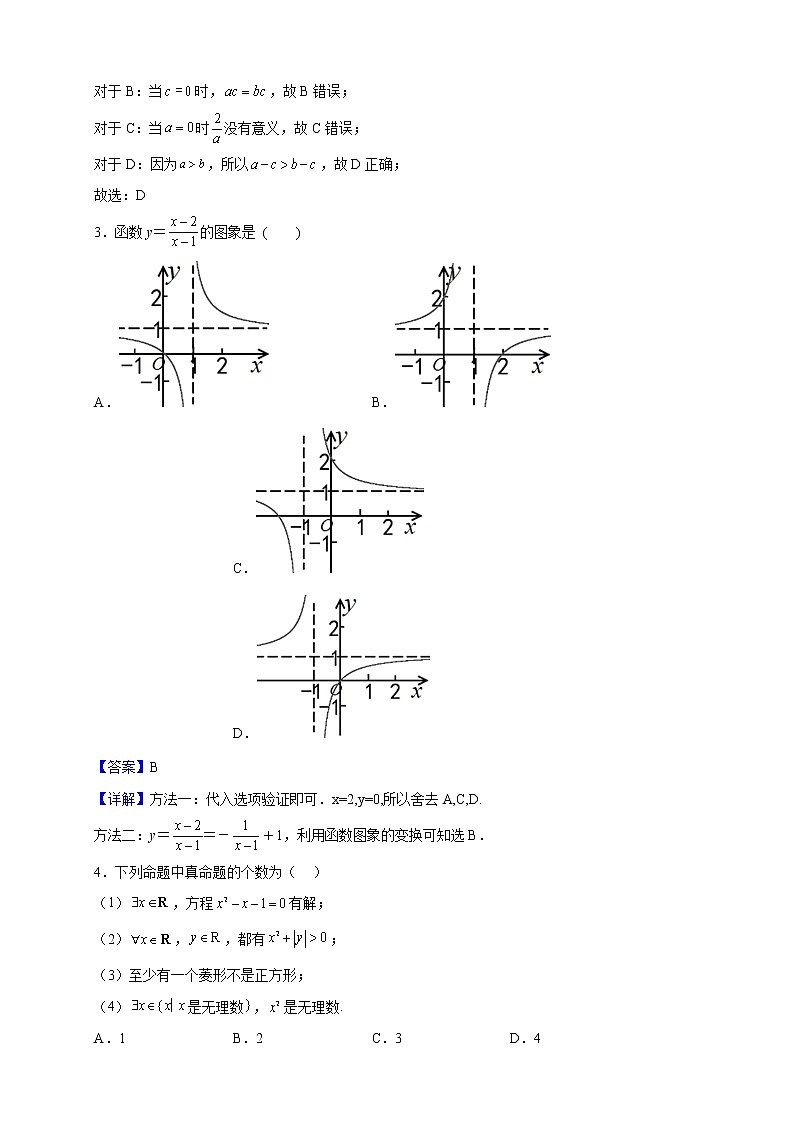
2022-2023学年山西省朔州市怀仁县第九中学高一上学期第一次月考数学试题 一、单选题1．如图所示，已知全集为，集合，，图中阴影部分表示的集合为(    )A． B． C． D．【答案】A【分析】先观察韦恩图，图中阴影部分表示的集合中的元素是在集合A中，但不在集合B中，得出图中阴影部分表示的集合，再结合已知条件即可求解．【详解】解：图中阴影部分表示的集合中的元素是在集合A中，但不在集合B中．由韦恩图可知阴影部分表示的集合为，又A＝{0，1，2，3，4，5}，，∴，∴．则图中阴影部分表示的集合是：．故选：A．2．设，且，则下列不等式一定成立的是（    ）A． B．C． D．【答案】D【分析】利用特殊值及不等式的性质判断可得；【详解】解：因为，对于A，若，，满足，但是，故A错误；对于B：当时，，故B错误；对于C：当时没有意义，故C错误；对于D：因为，所以，故D正确；故选：D3．函数y＝的图象是 (　　)A． B． C． D．【答案】B【详解】方法一：代入选项验证即可．x=2,y=0,所以舍去A,C,D.方法二：y＝＝－＋1，利用函数图象的变换可知选B．4．下列命题中真命题的个数为（    ）（1），方程有解；（2），，都有；（3）至少有一个菱形不是正方形；（4）是无理数，是无理数.A．1 B．2 C．3 D．4【答案】C【分析】根据一元二次方程的解法、绝对值和平方运算、菱形、有理数和无理数、全称量词命题、存在量词命题的知识对选项逐一分析，由此确定正确选项.【详解】（1）由于，所以方程有解，（1）正确.（2）当时，，（2）错误.（3）当菱形内角都不为时，菱形不是正方形，（3）正确.（4）是无理数，是无理数，（4）正确.所以正确的有个.故选：C5．王昌龄《从军行》中两句诗为“黄沙百战穿金甲，不破楼兰终不还”，其中后一句中“攻破楼兰”是“返回家乡”的（    ）A．充分条件 B．必要条件C．充要条件 D．既不充分也不必要条件【答案】B【分析】返回家乡的前提条件是攻破楼兰，即可得出结论.【详解】由题可知：“攻破楼兰”是“返回家乡”的必要不充分条件.故选：B6．若函数的定义域为R，则实数m的取值范围是（    ）A． B． C． D．【答案】B【分析】由题意，即不等式的解集为，分，，三种情况讨论，即得解【详解】函数的定义域为，即不等式的解集为（1）当时，得到，显然不等式的解集为；（2）当时，二次函数开口向下，函数值不恒大于0，故解集为不可能．（3）当时，二次函数开口向上，由不等式的解集为，得到二次函数与轴没有交点，即，即，解得；综上，的取值范围为故选：B7．若且的解集为，则关于x的不等式的解集为（    ）A． B． C． D．【答案】D【分析】可得，且，所以，不等式可变为，求解即可【详解】由的解集为，可得，且，所以，不等式可变为，即，解得或，所以的解集为，故选：D8．已知实数满足，，则的大小关系为（    ）A． B． C． D．【答案】A【分析】把给出的已知条件，右侧配方后可得，再把给出的两个等式联立消去后，得到，利用基本不等式可得，从而得到结果.【详解】因为所以，，即，所以，∴，∴即，故答案选A．【点睛】该题考查的是有关比较大小的问题，涉及到的知识点有利用作差比较法确定式子的大小的问题，属于简单题目. 二、多选题9．下列选项中的两个集合相等的有（    ）.A．B．C．D．【答案】AC【分析】分析各对集合元素的特征，即可判断.【详解】解：对于A：集合表示偶数集，集合也表示偶数集，所以，故A正确；对于B：，，所以，故B错误；对于C：，又，所以，即，所以，故C正确；对于D：集合为数集，集合为点集，所以，故D错误；故选：AC10．有以下判断，其中是正确判断的有（      ）A． 与 表示同一函数；B．函数 的图象与直线 的交点最多有 1 个C．函数 的最小值为 2D．若 ，则 【答案】BD【分析】利用两个函数的定义域可判断A；根据函数的定义可判断B；利用均值不等式等号成立的条件可判断C；将函数值代入可判断D【详解】选项A，函数定义域，函数定义域为R，故两个函数不是同一个函数，不正确；选项B，由函数定义，定义域中的每个只有唯一的与之对应，正确；选项C，，等号成立的条件是即，无解，所以等号不成立，不正确；选项D，，正确.故选：BD11．若，使得成立是假命题，则实数可能取值是（    ）A． B． C．3 D．【答案】AB【解析】首先由条件可知命题的否定是真命题，参变分离后，转化为最值问题求的取值范围.【详解】由条件可知，是真命题，即，即，设 等号成立的条件是，所以的最小值是，即，满足条件的有AB.故选：AB【点睛】关键点点睛：本题的关键首先是写出特称命题的否定，第二个关键是参变分离，转化为函数的最值求参数的取值范围.12．下列命题中真命题有（    ）A．若，则的最大值为2B．当，时，C．若，则的最大值为D．当且仅当a，b均为正数时，恒成立【答案】ABC【分析】结合基本不等式的知识对选项逐一分析，由此确定正确选项.【详解】A选项，，当且仅当时等号成立，A正确.B选项，，当且仅当时等号成立，B正确.C选项，则，，当且仅当时等号成立，C正确.D选项，当均为负数时，也成立，所以D选项错误.故选：ABC 三、填空题13．命题“对任意，都有”的否定为__________．【答案】存在，使得【详解】全称命题的否定为其对应的特称命题，则：命题“对任意，都有”的否定为存在，使得.14．含有三个实数的集合既可表示成，又可表示成，则__________.【答案】1【分析】根据集合相等求得值，然后计算．【详解】解：由题意，所以，即，所以，解得，当时，与元素互异性矛盾，舍去，时，两个集合为．满足题意．所以．故答案为：．15．若函数的定义域为，则函数的定义域为____________．【答案】【分析】由条件可得，，即可得到函数的定义域为，使有意义满足，，然后可建立不等式组求解.【详解】因为函数的定义域为，所以，，所以函数的定义域为，所以要使函数有意义，则有，解得，所以函数的定义域为.故答案为：16．，，使得成立，则实数m的范围______【答案】【分析】令，，根据题意得到，进而求出实数m的范围.【详解】令，，要想，，使得成立，只需，其中在单调递增，，在上单调递增，，故，解得：所以实数m的范围为故答案为： 四、解答题17．设集合，.（1）若，求实数的值；（2）若，求实数的取值范围.【答案】（1）；（2）或.【解析】（1）求得集合，由题意可得，可求得的值，再验证是否满足，由此可求得实数的值；（2）由题意可得，分、、、四种情况讨论，求得实数的值，并检验是否成立，由此可求得实数的取值范围.【详解】（1），因为，所以，所以，整理得，解得或.当时，，不满足；当时，，满足；故；（2）由题意，知，由，得.①当集合时，关于的方程没有实数根，所以，即，解得；②当集合时，，无解；③当集合时，，解得，④当时，，解得综上，可知实数的取值范围为或.【点睛】本题考查交集的计算，同时也考查了利用集合的包含关系求参数，考查分类讨论思想的应用与运算求解能力，属于中等题.18．求下列函数解析式：(1)已知，求的解析式．(2)已知，求的解析式．【答案】(1)(2) 【分析】（1）令 ，使用换元法求解析式；（2）令得，与原式组成方程组求解.【详解】（1）令，则所以所以综上所述，结论是:（2）令得，由解得综上所述，结论是:19．先后两次购买同一种物品，可采取两种不同的方式，第一种是不考虑物品价格的升降，每次购买该物品的数量一定；第二种是不考虑物品价格的升降，每次购买该物品所花的钱数一定.甲、乙二人先后两次结伴购买同一种物品，其中甲在两次购物时采用第一种方式，乙在两次购物时采用第二种方式.已知第一次购物时该物品单价为，第二次购物时该物品单价为（）.甲两次购物的平均价格记为，乙两次购物的平均价格记为.（1）求，的表达式（用表示）；（2）通过比较，的大小，说明哪种购物方式比较划算.【答案】（1）；（2）第二种购物方式比较划算.【解析】（1）求出总花费及购物总量后可得均价；（2）两者作差后可得大小．得出划算的方式．【详解】解：（1）设甲两次购物时购物量均为m，则两次购物总花费为m+m，购物总量为2m，平均价格为.设乙两次购物时用去钱数均为n，则两次购物总花费2n，购物总量为，平均价格为=综上，（2）∵，∴由此可知，第二种购物方式比较划算.20．（1）已知，．且，求的最小值；（2）已知x，y是正实数，且，求最小值．【答案】4；.【分析】（1）根据，结合基本不等式即可求得最小值；（2）由可得，利用“1”的代换结合基本不等式即可求得最小值.【详解】（1）因为，．且，则，当且仅当，即，或，时取等号.即的最小值为.（2）因为，所以，，当且仅当，即时取等号.即的最小值为.故答案为：4；.21．给定函数，，.(1)在所给坐标系（1）中画出函数，的大致图象；（不需列表，直接画出.）(2)，用表示，中的较小者，记为，请分别用解析法和图象法表示函数.（的图象画在坐标系（2）中）(3)直接写出函数的值域.【答案】(1)图象见解析.(2)，图象见解析.(3). 【分析】（1）根据函数的解析式，在坐标系中分别描出5个点，再将各点连接起来，即可得，的大致图象；（2）根据函数的定义，结合（1）所得图象写出解析式，进而画出的图象.（3）由（2）所得图象直接写出的值域.【详解】（1） -2-1012-6020-6-6-3036 ∴函数，的大致图象如下图示：（2）由，可得或，结合（1）的图象知：，则的图象如下：（3）由（2）所得图象知：的值域为.22．已知二次函数．(1)若时，不等式恒成立，求实数的取值范围．(2)解关于的不等式（其中）．【答案】(1)；(2)答案见解析. 【分析】(1)当时将原不等式变形为，根据基本不等式计算即可；(2)不等式化为，讨论的取值，从而求出对应不等式的解集．【详解】（1）不等式即为：，当时，不等式可变形为：，因为，当且仅当时取等号，所以，所以实数a的取值范围是.（2）不等式， 等价于，即，①当时，不等式整理为，解得；当时，方程的两根为，，②当时，可得，解不等式得或；③当时，因为，解不等式得；④当时，因为，不等式的解集为；⑤当时，因为，解不等式得；综上所述，不等式的解集为：①当时，不等式解集为；②当时，不等式解集为；③当时，不等式解集为；④当时，不等式解集为；⑤当时，不等式解集为．