山东省济南市长清区2022-2023学年九年级上学期期末数学试题

这是一份山东省济南市长清区2022-2023学年九年级上学期期末数学试题，共10页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
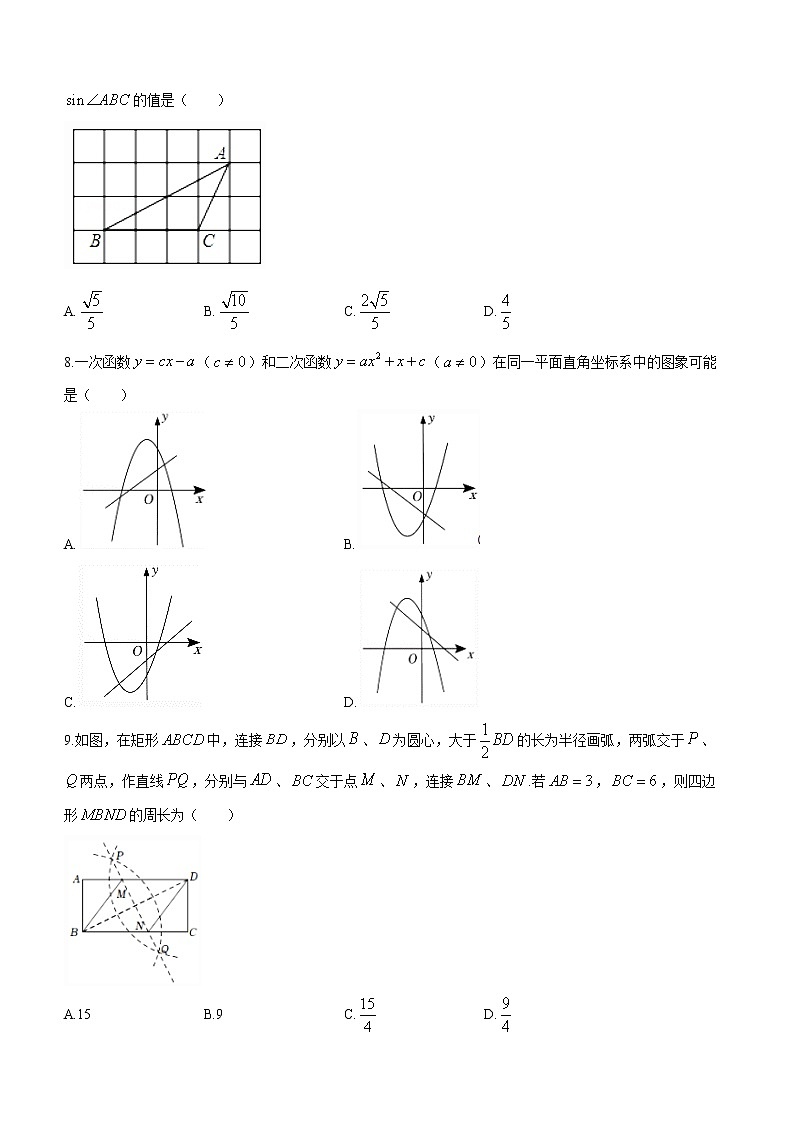
九年级阶段检测数学试题注意事项：本试题共8页，满分为150分，考试时间为120分钟.答卷前，请考生务必将自己的姓名、座号和准考证号填写在答题卡上，并将考点、姓名、准考证号和座号填写在试题规定的位置.考试结束后，仅交回答题卡.第Ⅰ卷（选择题  共40分）一、选择题（本大题共10小题，每小题4分，共40分.）1.的值为（    ）A. В. C. D.12.如图中几何体的左视图为（    ）A.  B.C.  D.3.如果，那么下列比例式中正确的是（    ）A. B. C. D.4.下列的各点中，在反比例函数图象上的点是（    ）A. B. C. D.5.关于的一元二次方程有两个相等的实数根，则的值为（    ）A. B. C.0 D.16.若点，，在反比例函数（）的图象上，则下列结论中正确的是（    ）A. B. C. D.7.如图，在网格正方形中，每个小正方形的边长为1，顶点为格点，若的顶点均是格点，则的值是（    ）A. B. C. D.8.一次函数（）和二次函数（）在同一平面直角坐标系中的图象可能是（    ）A. B.C.  D.9.如图，在矩形中，连接，分别以、为圆心，大于的长为半径画弧，两弧交于、两点，作直线，分别与、交于点、，连接、.若，，则四边形的周长为（    ）A.15 B.9 C. D.10.如图，已知开口向上的抛物线与轴交于点，对称轴为直线.下列结论：①；②；③若关于的方程一定有两个不相等的实数根；④.其中正确的个数有（    ）A.1个 B.2个 C.3个 D.4个二、填空题（本大题共6小题，每小题4分，共24分.）11.如图，四边形四边形，若，，，则______°.12.在一个不透明的袋子里装有若干个红球和6个黄球，这些球除颜色外都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则估计袋子中红球的个数是______个.13.如图，若点在反比例函数（）的图象上，轴于点，的面积为8，______.14.将抛物线向右移3单位，上移2单位所得到的新抛物线解析式为______.15.定义一种运算：，.例如：当，时，，则的值为______.16.如图，在正方形中，点、为边和上的动点（不含端点），，下列四个结论：①当时，则；②；③的周长不变；④若，，则的面积为15.其中正确结论的序号是______.三、解答题（本大题共10小题，共86分）17.（6分）计算：.18（6分）.19.（6分）如图，在菱形中，于点，于点，求证：.20.（8分）如图，，，，，.求的长度.21.（8分）某校为落实“双减”工作，增强课后服务的吸引力，充分用好课后服务时间，为学有余力的学生拓展学习空间，成立了5个活动小组（每位学生只能参加一个活动小组）：.音乐；.体育；.美术；.阅读；.人工智能.为了解学生对以上活动的参与情况，随机抽取部分学生进行了调查统计，并根据统计结果，绘制了如图所示的两幅不完整的统计图.根据图中信息，解答下列问题：（1）①此次调查一共随机抽取了______名学生；②补全条形统计图（要求在条形图上方注明人数）；③扇形统计图中圆心角______度；（2）若该校有2800名学生，估计该校参加组（阅读）的学生人数；（3）学校计划从组（人工智能）的甲、乙、丙、丁四位学生中随机抽取两人参加市青少年机器人竞赛，请用树状图法或列表法求出恰好抽中甲、乙两人的概率.22.（8分）为进一步加强疫情防控工作，长清区某学校决定安装红外线体温检测仪，对进入测温区域的人员进行快速测温（如图1），其红外线探测点可以在垂直于地面的支杆上下调节（如图2），已知探测最大角（）为61°，探测最小角（）为37°.若该校要求测温区域的宽度为1.4米，请你帮助学校确定该设备的安装高度.（参考数据：，，，，）23.（10分）某商店准备进一批季节性小家电，单价40元，经市场预测，销售定价为52元时，可售出180个.现在采取提高商品定价减少销售量的办法增加利润，定价每增加1元，销售量净减少10个.（1）商店若将准备获利2000元，则定价应增加多少元？（2）若商店要获得最大利润，则定价应增加多少元？最大利润是多少？24.（10分）如图，一次函数的图象与反比例函数（）的图象交于点，与轴交于点.点在反比例函数（）的图象上的一点，轴，垂足为，与交于点，.（1）求，的值；（2）若点为轴上的一点，求当最小时，点的坐标；（3）是平面内一点，是否存在点使得以、、、为顶点的四边形是平行四边形？若存在，请直接写出所有符合条件的点的坐标；若不存在，请说明理由.25.（12分）【发现问题】（1）如图1，已知和均为等边三角形，在上，在上，易得线段和的数量关系是______.（2）将图1中的绕点旋转到图2的位置，直线和直线交于点.①判断线段和的数量关系，并证明你的结论；②图2中的度数是______.【探究拓展】（3）如图3，若和均为等腰直角三角形，，，，直线和直线交于点，分别写出的度数，线段、间的数量关系，并说明理由.26.（12分）综合与探究：如图，抛物线（）与轴交于点和点，与轴交于点.（1）求此抛物线的函数表达式；（2）若点是第三象限抛物线上一动点，连接，，，求面积的最大值，并求出此时点的坐标；（3）若点在抛物线的对称轴上，线段绕点逆时针旋转90°后，点的对应点恰好也落在此抛物线上，请直接写出点的坐标.      九年级阶段检测数学试题答案一、选择题（本大题共10小题，每小题4分，共40分）题号12345678910答案ADCCDBABAD二、填空题（本大题共6小题，每小题4分，共24分.）11. 115   12. 2   13.   14.   15.   16.①③.三.解答题（本大题共10小题，共86分）17.（6分）计算：18.（6分）.公式法：算出，，因式分解法：，，配方法：，，19.（6分）证明：菱形，，，.（或者连接，证）.20.（8分）证明：，，，，，21.（8分）根据图中信息，解答下列问题：（1）①400；②60，60；③54（2）（人）答：参加组（阅读）的学生人数为280人（3）列表或画树状图正确共有12中等可能的结果，其中恰好抽到，两人同时参赛的有两种（恰好抽中甲、乙两人）22.（8分）方法1：解：在中，，设，则在中，，.经检验，是原方程的解方法2：解：在中，设，则在中，经检验，是原方程的解23.（10分）（1）解：设定价应增加元解得，采取提高商品定价减少销售量的办法增加利润不合题意舍去，答：定价应增加8元.（1）设定价增加元时获利元当时，有最大值，为2250元.答：若商店要获得最大利润，则定价应增加3元，最大利润是2250元.24.（10分）（1）求出，；（2）求出，画图找到点，求出点的坐标；（3），，25.（12分）【发现问题】（1）（2）①，证明过程  ②60度（3）写出度，证明过程26.（12分）（1）解出，，抛物线的函数表达式（2）求出点，直线关系式设点，过点作轴的垂线，交于点，则点，当时，S有最大值为，此时，（3），