高分突破，智取压轴小题01 探索分段函数的图象与性质（含答案解析）

这是一份高分突破，智取压轴小题01 探索分段函数的图象与性质（含答案解析），共34页。试卷主要包含了方法综述，解题策略，强化训练等内容，欢迎下载使用。
探索分段函数的图象与性质
一、方法综述
分段函数：对于自变量的不同的取值范围，有着不同的对应法则，这样的函数通常叫做分段函数．它是一个函数，而不是几个函数：分段函数的定义域是各段函数定义域的并集，值域也是各段函数值域的并集．
求分段函数的函数值时，应首先确定所给自变量的取值属于哪一个范围，然后选取相应的对应关系．若自变量值为较大的正整数，一般可考虑先求函数的周期．若给出函数值求自变量值，应根据每一段函数的解析式分别求解，但要注意检验所求自变量的值是否属于相应段自变量的范围．
对于分段函数应用题，尤其是求最值问题，不仅要分段考虑，最后还要再将各段综合起来进行比较．要注意分段函数值域是各段上函数值域的并集，最大(小)值是各段上最大(小)值中最大(小)的．[来源:Zxxk.Com]
二、解题策略
类型一：分段函数的图象
例1．已知函数是定义在上的奇函数，当时，.若对任意的，成立，则实数的取值范围是（ ）
A． B． C． D．
【来源】江西省南昌市第十中学2021届高三上学期第二次月考数学（文）试题
【答案】D
【解析】由题设知：，又是定义在上的奇函数，即，∴当时，，即，而；
当时，，即，而；
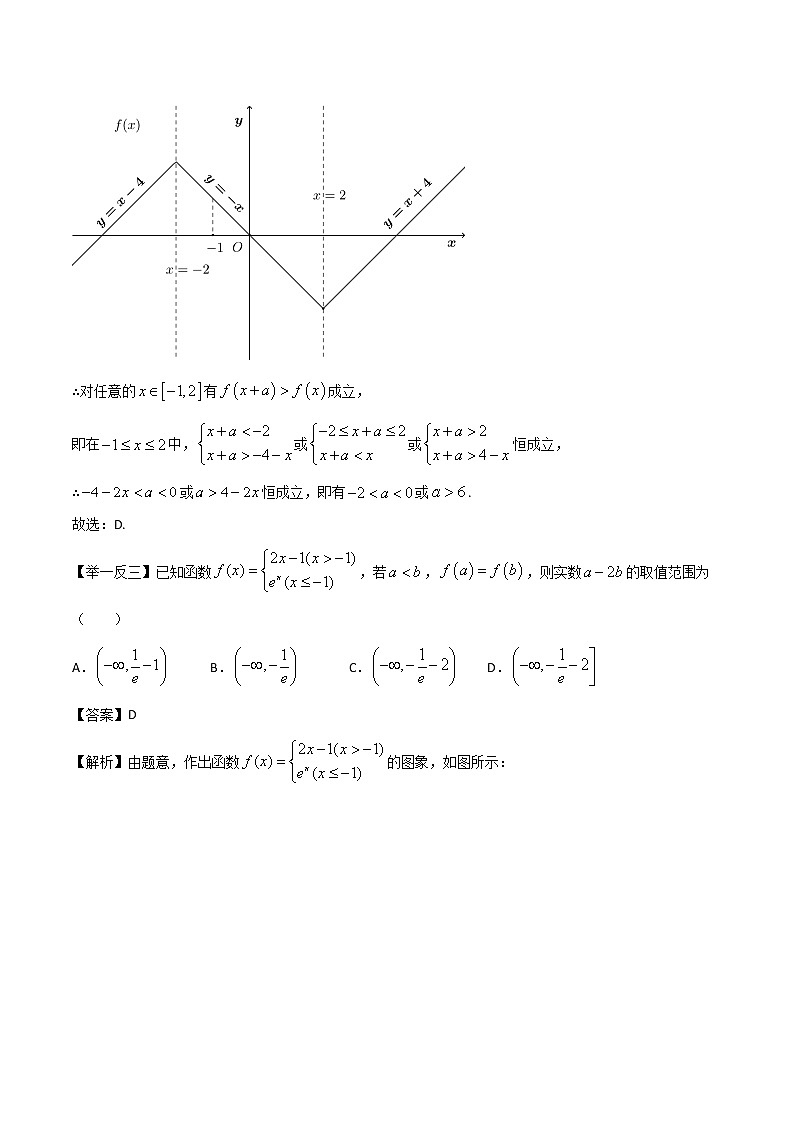
∴综上，有，可得如下函数图象，

∴对任意的有成立，
即在中，或或恒成立，
∴或恒成立，即有或.
故选：D.
【举一反三】已知函数，若，，则实数的取值范围为（ ）
A． B． C． D．
【答案】D
【解析】由题意，作出函数的图象，如图所示：

若，，则，则，，
令，，则，，
此时，则恒成立，所以函数单调递增，
所以，所以实数的取值范围为.
故选：D.
类型二：分段函数的零点
例2．已知函数，若函数恰有4个不同的零点，则实数的取值范围是________.
【来源】陕西省宝鸡市长岭中学2020-2021学年高三上学期期中理科数学试题
【答案】
【解析】当时，令，得，即，该方程至多两个根；
当时，令，得，该方程至多两个根，因为函数恰有4个不同的零点，所以函数在区间和上均有两个零点，函数在区间上有两个零点，即直线与函数在区间上有两个交点，
当时，；
当时，，此时函数的值域为，则，解得，
若函数在区间上也有两个零点，令，解得，，
则，解得，
综上所述，实数的取值范围是.
【举一反三】已知函数（，且）在区间上为单调函数，若函数有三个不同的零点，则实数a的取值范围是（ ）
A． B． C． D．
【答案】D
【解析】，当时，，
易知：在时单调递减，又在区间上为单调函数，
且，解得：，
令，即，
令，则函数有三个不同的零点，
等价于与有三个不同的交点，分别画出与的图象如下所示：

由图可知：当时，与有个不同的交点，
故只需满足：当时，与有个不同的交点，
即当时，，化简得：，即，
令，即与有一个交点，
画出的图象如下图所示：

易知，，
或，解得：，或，又，即或，
综上所述：.
故选：D.
类型三：分段函数的奇偶性
例3．【2020·江西高三月考】已知定义域为R的奇函数，当时，满足，则　　
A． B． C． D．0
【答案】B
【解析】定义域为的奇函数，可得，
当时，满足，
可得时，，则，
，，
，，
，，
，

， 故选B.
【名师点睛】判断函数奇偶性的方法通常有：

【举一反三】【2020•达州模拟】f（x）是定义域为R的偶函数，对∀x∈R，都有f（x+4）＝f（﹣x），
当0≤x≤2时，，则＝　　．
【答案】
【解析】根据题意，f（x）是定义域为R的偶函数，对∀x∈R，都有f（x+4）＝f（﹣x），
则有f（x+4）＝f（x），即函数f（x）是周期为4的周期函数，
则有f（﹣）＝f（）＝f（4+）＝f（），f（21）＝f（1+4×5）＝f（1），
又由当0≤x≤2时，，
则f（）＝﹣1，f（1）＝1，则＝f（）+f（1）＝（﹣1）+1＝；
类型四：分段函数的单调性
例4．已知函数，若在上是增函数，则实数的取值范围是________．
【答案】
【解析】因为函数在上是增函数，所以在区间上是增函数且在区间上也是增函数，对于函数在上是增函数，
则；①
对于函数，
（1）当时，，外函数为定义域内的减函数，
内函数在上是增函数，
根据复合函数“同增异减”可得时函数在区间上是减函数，不符合题意，故舍去，
（2）当时，外函数为定义域内的增函数，要使函数在区间上是增函数，则内函数在上也是增函数，
且对数函数真数大于0，即在上也要恒成立，所以， 又，所以，②
又在上是增函数则在衔接点处函数值应满足：
，化简得，③
由①②③得，，所以实数的取值范围是.
【举一反三】【2019·江西省奉新县第一中学高三月考】已知f（x）是定义在R上的奇函数，且当x>0时在R上是单调函数，则实数a的最小值是 .
【答案】
【解析】当时，,,又f（x）是定义在R上的奇函数,
,因为在R上是单调函数
，最小值-1,故答案为.
三、强化训练
1．定义在上的函数满足，且当时，若对任意的，不等式恒成立，则实数的最大值为（ ）
A． B． C． D．
【答案】C
【解析】当时，单调递减，，
当时，单调递减，，
故在上单调递减，
由，得的对称轴为，
若对任意的，不等式恒成立，
即对，不等式恒成立，
，
即，
即，

故实数的最大值为.
故选：C.
2．函数若，且，则的取值范围是（ ）
A． B． C． D．
【来源】安徽省合肥一六八中学2020-2021学年高一上学期期末数学试题
【答案】B
【解析】画出函数的图象如图，
因为，且，
由图可知点的横坐标分别为，
其中，
因为的图象关于对称，
所以，又
所以
，
因为，所以，
即的取值范围是，
故选：B.

3．定义在R上的函数满足，当时，函数．若，，不等式成立，则实数m的取值范围是（ ）
A． B． C． D．
【答案】C
【解析】∵当x∈[0，2）时，
∴x∈[0，2），为最大值，
∵f（x+2）＝f（x），
∴f（x）＝2f（x+2），
∵，
∴
，
，



x∈[﹣2，0]，
∴，
，

，
∴，
∵函数g（x）＝x3+3x2+m，
∴
由3x2+6x＞0解得x＞0或，
由3x2+6x＜0解得
由3x2+6x＝0，x＝0或，
∴函数g（x）＝x3+3x2+m，在上单调递增．
在上单调递减，
，
∵不等式f（s）﹣g（t）≥0，
∴﹣8≥m﹣16，
故实数满足：m≤8，故选：C
4．已知函数若（，，，互不相等），则的取值范围是（注：函数在上单调递减，在上单调递增）（ ）
A． B． C． D．
【来源】河南省天一大联考2020-2021学年高一上学期期末数学试题
【答案】D
【解析】作出函数的图象如下图所示：设，且，当时，即，所以，所以，
当时，解得，，所以
设，又函数在上单调递增，
所以，即，
所以，即，
故选：D．

5．若关于的方程有四个不同的实数解，则实数的取值范围为（ ）
A． B． C． D．
【答案】D
【解析】由于关于的方程有4个不同的实数解，当时，是此方程的1个根，
故关于的方程有3个不同的非零的实数解，
又
即方程有3个不同的非零的实数解，
即函数的图像与函数的图像有3个不同的交点，在同一直角坐标系作图：

由图可知，，即，的取值范围为
故选：D
6．已知函数，则函数的零点个数是 （ ）
A．4 B．5 C．6 D．7
【答案】A
【解析】令，则，
作出的图象和直线，由图象可得有两个交点，设横坐标为，

∴.
当时，有，即有一解；当时，有三个解，
∴综上，共有4个解，即有4个零点.故选：A
7．对于，定义运算“”：，设，且关于的方程恰有三个互不相等的实数根，则的取值范围是（ ）
A． B．
C． D．(1,2)
【答案】A
【解析】由题设知
化简整理得：，画出函数的图像，如下图

由，当关于的方程恰有三个互不相等的实数根时，t的取值范围是，
设，则是的两个根，关于对称，故，
下面求的范围：，解得：
，，，故
所以
故选：A.
8．已知函数，对，使得成立，则的取值范围是（ ）
A． B．
C． D．
【来源】吉林市普通高中2021届高三第一次调研测试（期中）数学（文）试题
【答案】D
【解析】时，



，使得成立

对函数
当时，，此时
当时，

令得
当时，，单调递减
当时，，单调递增
所以为极小值点，此时
故
当，不合题意；
当，
所以，解得
当，
所以，解得
综上得
故选：D.
9．已知函数，若函数恰有两个零点，，则的取值范围是（ ）
A． B． C． D．
【来源】浙江省名校协作体2020-2021学年高三上学期开学考试数学试题
【答案】C
【解析】由的解析式知：，
∴若函数恰有两个零点，，有两种情况：
1、当时，在上没有零点；在上要有两个零点，则即符合前提条件，此时，；
2、当时，在上有一个零点为-1；在上要有一个零点即可，则即；故有，此时
∴综上，有：；
故选：C
10．设，若，则（ ）.
A．1 B． C． D．
【来源】安徽省蚌埠市2020-2021学年高三上学期第一次质量监测理科数学试题
【答案】C
【解析】由题意，函数，
当时，可得，，所以，
可得，解得，所以；
当时，可得，，所以，
可得，即，
设，则，单调递减，且，
方程无实根，即方程无解，
综上可得，.
故选：C.
11．设min{m，n}表示m，n二者中较小的一个，已知函数f(x)＝x2＋8x＋14，g(x)＝(x>0)，若∀x1∈[－5，a](a≥－4)，∃x2∈(0，＋∞)，使得f(x1)＝g(x2)成立，则a的最大值为
A．－4 B．－3 C．－2 D．0
【来源】黑龙江省哈尔滨师范大学青冈实验中学校2019-2020学年高三10月月考数学（理）试题
【答案】C
【解析】令，解得，故当时，，当时，，所以.所以当时，函数的值域为，当时，的值域为，所以的值域为.函数，它的图像开口向上，对称轴为，则当时，函数在上的值域为，是的子集，符合题意.当时，函数在上的值域为，它是的子集，故，解得.综上所述，满足题意的的取值范围是.所以的最大值为，故选C.
12．若函数的值域为，则的取值范围为（ ）
A．， B．， C．， D．，，
【来源】吉林省通钢一中、集安一中、梅河口五中等省示范高中2020届高三（5月份）高考数学（文科）模拟试题
【答案】B
【解析】①若时，则当时，单调递增，
当时，在上单调递增，
在，上单调递减，
若函数值域为则需，解得；
②若时，
则当时，单调递减，
当时，在上单调递增，在，上单调递减，不满足函数值域为，不符合题意，舍去，
综上：的取值范围为，，
故选：
13．已知函数，方程有四个不同根，，，，且满足，则的取值范围是
A． B． C． D．
【来源】安徽省宿州市泗县第一中学2020届高三下学期最后一卷数学（文）试题
【答案】D
【解析】
作出函数图像可得，从而得，且，从而得，所以，令则，在上递增，所以.
故选：D.
14．设函数，若有最小值，则实数a的取值范围为（ ）
A． B． C． D．
【来源】湖南省衡阳市2020届高三下学期三模数学（理）试题
【答案】D
【解析】因为当时，无最小值，且，
只需当时，有最小值，且即可.
当时，，因为
若时，，在上递增，此时无最小值；
若时，，记两根分别为，，设，因为，
则，又，所以 ，
故在上递减，在上递增，
此时，
将代入得，
解得，所以，
故选：D.
15．已知函数，若方程有2个不同的实根，则实数的取值范围是（ ）
A．或 B．或或
C．或 D．或
【答案】B
【解析】由题意，可画出与的图象有如下情况
1、当时，显然与无交点，
若与有交点，则有，
即，故此时有2个不同的实根；如下图示

2、当时，显然与无交点，
而在上有，故此时只有一个的实根；如下图示

3、当时，显然与无交点，而在上有，故此时有2个不同的实根；如下图示

4、当时，显然与恒有一个交点，
而此时在上若与相切则有2个不同的实根，
即有，故、过，则，显然不成立，
故此时只有一个的实根；如下图示

5、当时，由4中的结论可知有2个不同的实根；如下图示

6、当时，显然与恒有一个交点，
而由5知与恒有两个交点，
故此时有3个不同的实根；如下图示

故综上，有或或时，有2个不同的实根
故选：B
16．已知函数若存在实数，满足，且，则的最大值为（ ）
A． B． C． D．
【答案】B
【解析】的图象如下

存在实数，满足，且，即
∴，则
令，，则
∴在上单调递增，故
故选：B
17．已知函数，，，若对于任意，总存在，使成立，则实数的取值范围是（ ）
A． B．
C． D．
【来源】开卷教育联盟2020届全国高三模拟考试（四）数学理科试题
【答案】D
【解析】当时，，，即，为增区间，，，
当时，；
当时，，，此时函数递增，则，．
则的值域为，，．
对于任意，，总存在，，使得成立，
得到函数在，上的值域是在，上值域的子集．
对讨论，当时，，显然不成立；
当时，的值域为，，由且，即；
当时，的值域为，，由且，即，
综上，的取值范围是：，，．
故选：D.
18．已知是定义在R上的函数，且关于直线对称.当时， ，若对任意的，不等式恒成立，则实数的取值范围是（ ）
A． B． C． D．
【答案】D
【解析】当时，，函数在上单调递减，且是R上的增函数，根据复合函数的单调性可知，函数在上单调递减，且；
当时，，易知函数在上单调递减，且.
∴函数在上单调递减.
∵关于直线对称，∴关于对称，即为偶函数，
∴不等式可化为，
∴恒成立，
即，整理得，
令，
∴对任意的，恒成立，
∴，
即，解得.
故选：D.
19．把方程表示的曲线作为函数的图象，则下列结论正确的是（ ）
①在R上单调递减
②的图像关于原点对称
③的图象上的点到坐标原点的距离的最小值为3
④函数不存在零点
A．①③ B．①②③ C．①③④ D．①②③④
【来源】黑龙江省哈尔滨市2020届高三5月模拟复课联考数学（理）试题
【答案】C
【解析】，当，时不成立；当，时，；
当，时，；当，时，；
画出图像，如图所示：

由图判断函数在R上单调递减，故①正确，②错误.
由图判断图象上的点到原点距离的最小值点应在，的图象上，
即满足，设图象上的点，
，当时取最小值3，故③正确；
当，即，函数的零点，就是函数和的交点，而是曲线，，和，，的渐近线，所以没有交点，
由图象可知，和，，没有交点，
所以函数不存在零点，故④正确.
故选：C.
20．定义函数为不大于的最大整数，对于函数有以下四个命题：①；②在每一个区间，上，都是增函数；③；④的定义域是，值域是.其中真命题的序号是（ ）.
A．③④ B．①③④ C．②④ D．①②④
【答案】D
【解析】画出的图象如图所示，

由函数的图象可知，是最小正周期为1的函数，且当时，，
所以，所以①②④都正确，
而，，所以③错误.
故选：D
21．函数，，若存在使得成立，则整数的最小值为
A． B．0 C．1 D．2
【来源】贵州省毕节市2020届高三诊断性考试（三）理科数学试题
【答案】B
【解析】由题意得，即，所以函数为偶函数，且函数，满足，所以函数为偶函数，
要使得存在使得成立，
只需当时，有解，即在有解，
即在有解，
令，则，
当时，，函数单调递减；
当时，，函数单调递增；
所以当时，函数取得最小值，
要使的使得存在使得成立，可得，
所以整数的最小值为0.
故选：B.
22．已知函数，则方程的实数根的个数为（ ）
A．5 B．6 C．7 D．8
【答案】B
【解析】作出函数的大致图象如图（1）所示，对于，令，则，则或或或，作出函数的大致图象，如图（2）所示，

若，则由图象知，直线与函数的图象有两个交点；若，由图象知，直线与函数的图象有四个交点；
显然直线与函数的图象没有交点，
综上可知，方程的实数根的个数为.
故选：B
23．已知函数给出下列四个结论：
①存在实数，使函数为奇函数；
②对任意实数，函数既无最大值也无最小值；
③对任意实数和，函数总存在零点；
④对于任意给定的正实数，总存在实数，使函数在区间上单调递减.其中所有正确结论的序号是______________.
【来源】中国人民大学附属中学2021届高三3月开学检测数学试题
【答案】① ② ③ ④
【解析】

如上图分别为，和时函数的图象，
对于① ：当时，，
图象如图关于原点对称，所以存在使得函数为奇函数，故①正确；
对于② ：由三个图知当时，，当时，，所以函数既无最大值也无最小值；故② 正确；
对于③ ：如图和图中存在实数使得函数图象与没有交点，此时函数没有零点，所以对任意实数和，函数总存在零点不成立；故③ 不正确
对于④ ：如图，对于任意给定的正实数，取即可使函数在区间上单调递减，故④正确；
故答案为：① ② ④
24．函数，若存在a，b，c（），使得，则的最小值是________.
【来源】广东省清远市2021届高三上学期11月摸底数学试题
【答案】.
【解析】设，则，，，且，
由，得，由，得，
所以，
设，则，，
设，则，
所以在单调递减，在单调递增，
所以，故的最小值是.
故答案为：.

25．已知函数和.若对任意的，都有使得，，则实数的取值范围是______.
【答案】
【解析】由题意得， ,并且对于值域中的每一个数，都有至少两个不同数和，使得成立.
①当时， 在上单调递减，显然，此种情况不成立.
②当，在上的值域为，由的函数图象可知，只要使得，则解得.
③当时，在上的值域为，由的函数图象可知，要满足即可，得，综上所述，.

26．已知函数，若关于的不等式在上恒成立，则实数的取值范围是__________.
【答案】
【解析】作出函数的图象如图所示，

当时，恒成立，符合题意；
当时，，，关于的不等式不恒成立，不合题意，舍去；
当时，大致图象如图中折线，
只需恒成立，且恒成立即可，
且即，
且，
所以，
综上所述.
27．已知函数若f(x)的值域为(0，+∞)，则实数a的取值范围是________．
【答案】或
【解析】当时，，
若，则当时，，这与函数的值域为矛盾，
若，则当时，，因为函数的值域为，
故，令，则且即，
令，则，
当时，，当，，
故在上为增函数，在上为减函数，
又，故即，所以，
所以 ，而，
故的解为或，
故或.
28．设m≠-1，函数则使得成立的实数m的个数为__________.
【来源】广西桂林市广西师范大学附属2021届高三年级上学期数学第三次月考试题
【答案】1
【解析】根据题意，设，所以，，
所以，，
当即时，，，即，令， ，即求两个函数图象交点个数，画出图象，

只有一个解，只有一个解；
当即时，，，即，
令， ，即求两个函数图象交点个数，画出图象，

无交点，即无解；
故答案为：1. .