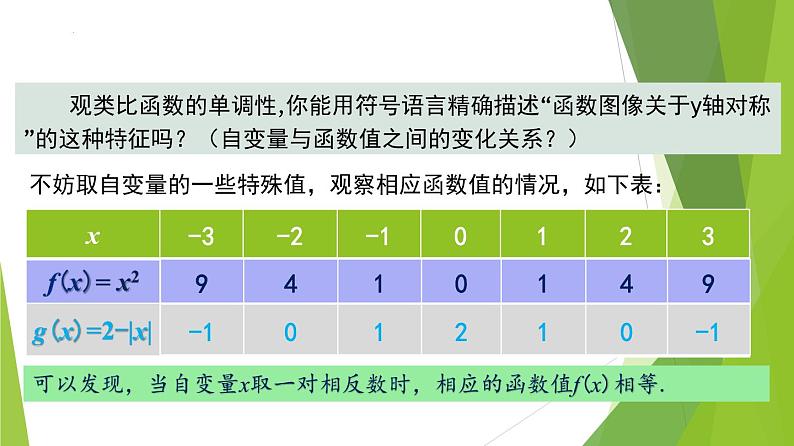
高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质备课ppt课件

这是一份高中数学人教A版 (2019)必修 第一册3.2 函数的基本性质备课ppt课件，文件包含322奇偶性教学课件-2022-2023学年高一数学同步备课系列人教A版2019必修第一册pptx、322奇偶性分层作业-2022-2023学年高一数学同步备课系列人教A版2019必修第一册解析版docx、322奇偶性分层作业-2022-2023学年高一数学同步备课系列人教A版2019必修第一册原卷版docx等3份课件配套教学资源，其中PPT共40页， 欢迎下载使用。
3.2.2 奇偶性（分层作业）（夯实基础+能力提升）【夯实基础】一、单选题1．（2021·山西大同·高一期中）已知函数f（x）为定义在R上的奇函数，下列说法错误的是（    ）A．在R上，B．在R上，C．存在D．存在2．（2021·全国·高一专题练习）给出下列四个关于函数的命题：①（）与（）表示相同函数；②是既非奇函数也非偶函数；③若与在区间上均为递增函数，则在区间上亦为递增函数；④设集合，，对应关系，则能构成一个函数，记作，.其中，真命题为（    ）A．②③ B．①④ C．①③④ D．②③④3．（2022·河南安阳·高一期末）对于函数，，“”是“的图象既关于原点对称又关于轴对称”的（    ）A．充分不必要条件 B．必要不充分条件C．充要条件 D．既不充分也不必要条件4．（2022·全国·高一课时练习）下列说法中错误的是（    ）A．奇函数的图像关于坐标原点对称 B．图像关于轴对称的函数是偶函数C．奇函数一定满足 D．偶函数的图像不一定与轴相交5．（2022·全国·高一课时练习）已知，且是定义在R上的奇函数，，则（    ）A．是奇函数 B．是偶函数C．既是奇函数又是偶函数 D．既不是奇函数也不是偶函数二、多选题6．（2021·广东·揭阳华侨高中高一期中）奇函数在的图像如图所示，则下列结论正确的有（    ）A．当时B．函数在上单调递减C．D．函数在上单调递增7．（2021·江西省乐平中学高一阶段练习）函数的图象是折线段，如图所示，其中点，，的坐标分别为，，，以下说法正确的是（    ）A．B．的定义域为C．为偶函数D．若在上单调递增，则的最小值为18．（2021·江苏·泗阳县实验高级中学高一阶段练习）已知定义域为的偶函数的一个单调递增区间是，关于函数的下列说法中正确的是（    ）A．一个递减区间是 B．一个递增区间是C．其图象对称轴方程为 D．其图象对称轴方程为9．（2021·重庆市云阳县双江中学校高一阶段练习）下列命题中说法正确的是（   ）A．空集是任何集合的子集B．函数在定义域上单调递减C．若在定义域上为奇函数，则一定有D．若具有奇偶性，则其定义域一定关于原点对称10．（2021·广东·高一期中）关于函数的说法正确的是（   ）A．值域为 B．C．该函数为偶函数 D．在上为增函数11．（2022·江苏南京·高一期末）已知函数，对于任意，则A．的图象经过坐标原点 B．C．单调递增 D．三、填空题12．（2021·全国·高一课时练习）给出下列结论：①若的定义域关于原点对称，则是偶函数；②若是偶函数，则它的定义域关于原点对称；③若，则（）是偶函数；④若（）是偶函数，则；⑤若，则（）不是偶函数；⑥既是奇函数又是偶函数的函数一定是（）；⑦若是定义在上的奇函数，则．其中正确的结论是______（填序号）．13．（2021·全国·高一课时练习）定义，表示不大于x的最大整数（如，）.给出以下四个命题：①是定义在R上的奇函数；②是定义在R上的增函数；③在R上有最大值和最小值；④对任意、，都有.其中，真命题的序号是______.14．（2021·全国·高一专题练习）请写出一个同时满足下列三个条件的函数：（1）是偶函数；（2）在上单调递减；（3）的值域是.则__________.15．（2022·全国·高一课时练习）若函数是奇函数，则实数a的值为___________.16．（2022·全国·高一课时练习）已知是偶函数，当时，，则当时，_________．17．（2022·全国·高一课时练习）已知是定义在上的奇函数，且，则与的大小关系是______．（填“>”“=”或“<”）   四、解答题18．（2021·全国·高一专题练习）如图是函数f(x)＝在区间[0，＋∞)上的图象，请据此在该坐标系中补全函数f(x)在定义域内的图象，请说明你的作图依据．19．（2022·湖南·高一课时练习）若偶函数在区间上递减且在区间上递增，试讨论在区间上的增减性，并进一步讨论为奇函数的情形．    20．（2021·江苏·高一课时练习）求证：（1）是上的偶函数；（2）是上的奇函数.   21．（2022·全国·高一专题练习）已知是定义在上的奇函数，当时，．(1)求时，函数的解析式；(2)若函数在区间上单调递增，求实数的取值范围．     22．（2022·贵州贵阳·高一期末）已知函数是上的偶函数，当时，.(1)用单调性定义证明函数在上单调递增；(2)求当时，函数的解析式.     23．（2022·全国·高一专题练习）定义在上的单调增函数满足：对任意都有成立(1)求的值；(2)求证：为奇函数；(3)若对恒成立，求的取值范围．    24．（2022·湖南·高一课时练习）已知函数满足．(1)求的值；(2)求证：；(3)若，求的值．     25．（2022·湖南·高一课时练习）求证：定义于R上的两个奇函数的乘积是偶函数．       【能力提升】一、多选题1．（2022·全国·高一课时练习）已知函数，均为定义在上的奇函数，且，，则（    ）A．是奇函数 B．是奇函数C．是偶函数 D．是偶函数2．（2022·辽宁·东北育才学校高一阶段练习）已知函数的定义域为，是奇函数，则使得成立的充分条件是（    ）A．在上单调 B．为偶函数C．为偶函数 D．3．（2022·全国·高一课时练习）已知函数的定义域为R，且为奇函数，为偶函数，且对任意的，且，都有，则下列结论正确的是（    ）A．是奇函数 B．C．的图像关于对称 D．4．（2022·全国·高一期中）函数的图象可能为（    ）A． B．C． D．二、填空题5．（2022·全国·高一课时练习）已知函数是偶函数，是奇函数，它们的定义域均为，且它们在上的图像如图所示，则不等的解集是______．6．（2022·全国·高一单元测试）已知是定义在上的奇函数，且，若对任意，，且，有，则的最小值为______．7．（2022·全国·高一课时练习）已知函数的定义域为R，为偶函数，为奇函数，且当时，．若，则______． 三、解答题8．（2022·浙江·温州市第二十二中学高一开学考试）函数，(1)若在上是奇函数，求的值；(2)当时，求在区间上的最大值和最小值；(3)设，当时，函数既有最大值又有最小值，求的取值范围（用表示）    9．（2022·全国·高一课时练习）设函数，．(1)某同学认为，无论实数a取何值，都不可能是奇函数，该同学的观点正确吗？请说明你的理由．(2)若是偶函数，求实数a的值．(3)在（2）的情况下，恒成立，求实数m的取值范围．     10．（2022·全国·高一课时练习）已知函数是定义在R上的奇函数，且当时，．(1)求当x＞0时，函数的解析式；(2)解不等式．     11．（2022·全国·高一课时练习）已知函数是定义在上的奇函数，且.(1)求函数的解析式；(2)判断函数在上的单调性，并用定义证明；(3)解不等式：.     12．（2022·全国·高一课时练习）已知“函数的图象关于原点成中心对称图形”的充要条件是“函数为奇函数”，可以推广为：“函数的图象关于点成中心对称图形”的充要条件是“函数为奇函数”．(1)若函数满足对任意的实数m，n，恒有，求的值，并判断此函数的图象是否是中心对称图形．若是，请求出对称中心的坐标；若不是，请说明理由．(2)若（1）中的函数还满足当时，，求不等式的解集．           13．（2022·全国·高一课时练习）设函数对任意，都有，证明：为奇函数．     14．（2022·安徽省六安中学高一期末）已知函数是定义在上的奇函数，且.(1)求，的值；(2)判断在上的单调性，并用定义证明；(3)设，若对任意的，总存在，使得成立，求实数的取值范围.    15．（2022·河南·信阳高中高一期末）已知函数，且函数是偶函数，设(1)求的解析式；(2)若不等式≥0在区间(1，e2]上恒成立，求实数的取值范围；(3)若方程有三个不同的实数根，求实数的取值范围．