河北省邯郸市大名县第一中学2022-2023学年九年级上学期期末考试数学试题

这是一份河北省邯郸市大名县第一中学2022-2023学年九年级上学期期末考试数学试题，共25页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
河北省邯郸市大名县第一中学2022-2023学年九年级上学期期末考试数学试题
学校:___________姓名：___________班级：___________考号：___________

一、单选题
1．如图是由七个完全相同的小正方体组成的立体图形，则它的俯视图是（    ）

A． B．
C． D．
2．已知，那么的值为（    ）
A． B． C． D．
3．将二次函数的图象向右平移个单位长度，再向下平移个单位长度得到的二次函数解析式是（    ）
A． B．
C． D．
4．在中，，，，那么的值是（    ）
A． B． C． D．
5．已知反比例函数，下列结论中不正确的是（    ）
A．其图象经过点 B．其图象分别位于第一、第三象限
C．当时， D．当时，随的增大而增大
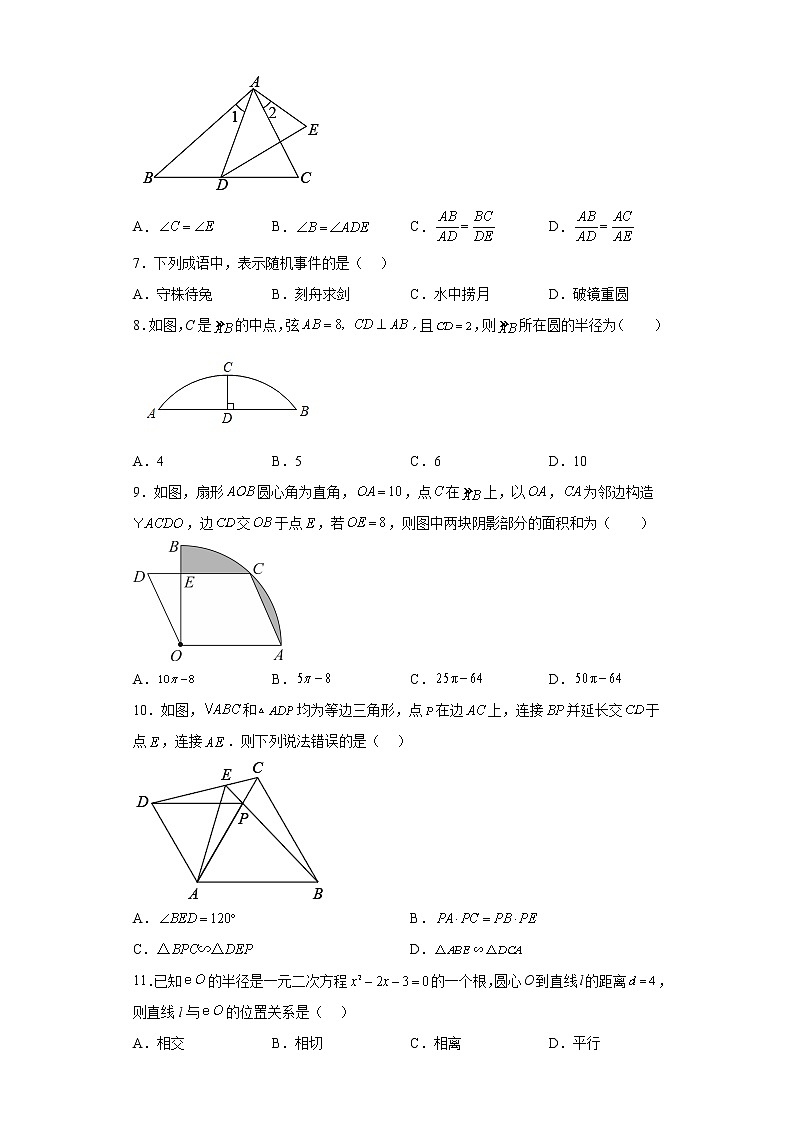
6．如图，已知，那么添加下列一个条件后，仍无法判定的是（    ）

A． B． C． D．
7．下列成语中，表示随机事件的是（    ）
A．守株待兔 B．刻舟求剑 C．水中捞月 D．破镜重圆
8．如图，C是的中点，弦，且，则所在圆的半径为（　　）

A．4 B．5 C．6 D．10
9．如图，扇形圆心角为直角，，点在上，以，为邻边构造，边交于点，若，则图中两块阴影部分的面积和为（　　）

A． B． C． D．
10．如图，和均为等边三角形，点在边上，连接并延长交于点，连接．则下列说法错误的是（    ）

A． B．
C． D．
11．已知的半径是一元二次方程的一个根，圆心O到直线l的距离，则直线l与的位置关系是（    ）
A．相交 B．相切 C．相离 D．平行
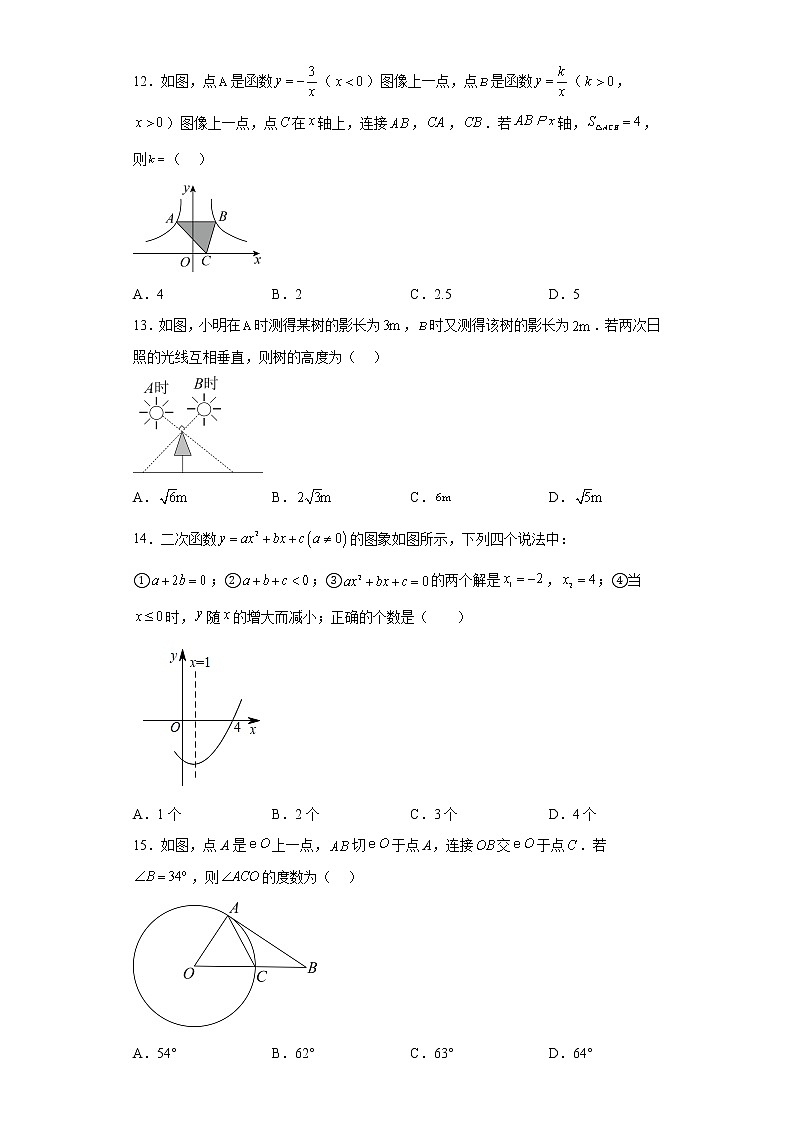
12．如图，点是函数（）图像上一点，点是函数（，）图像上一点，点在轴上，连接，，．若轴，，则（    ）

A．4 B．2 C．2.5 D．5
13．如图，小明在时测得某树的影长为，时又测得该树的影长为．若两次日照的光线互相垂直，则树的高度为（    ）

A． B． C． D．
14．二次函数的图象如图所示，下列四个说法中：
①；②；③的两个解是，；④当时，随的增大而减小；正确的个数是（　　）

A．1个 B．2个 C．3个 D．4个
15．如图，点A是上一点，切于点A，连接交于点．若，则的度数为（    ）

A．54° B．62° C．63° D．64°
16．“二十四节气”是中华上古农耕文明的智慧结晶，被国际气象界普为“中国第五大发明”，小文购买了“二十四节气”主题邮票，他要将“立春”“立夏”“秋分”“大暑”四张邮票中的两张送给好朋友小乐．小文将它们背面朝上放在桌面上（邮票背面完全相同），让小乐从中随机抽取一张（不放回），再从中随机抽取一张，则小乐抽到的两张邮票恰好是“立春”和“立夏”的概率是（    ）

A． B． C． D．

二、填空题
17．木箱里装有仅颜色不同的8张红色和若干张蓝色卡片，随机从木箱里摸出1张卡片记下颜色后再放回，经过多次的重复试验，发现摸到蓝色卡片的频率稳定在0.6附近，则估计木箱中蓝色卡片有___________张．
18．如图，在等边三角形ABC中，点D、点E分别在BC，AC上，且∠ADE＝60°，

（1）写出和∠CDE相等的角：______；
（2）若AB＝3，BD＝1，则CE长为______．
19．已知一次函数y＝ax+b（ab≠0）和二次函数y＝a+bx﹣2，其中一次函数的图象经过第一、三、四象限．
（1）二次函数图象在y轴的左侧部分，y随x的增大而_____；
（2）二次函数图象的顶点所在的象限是第_____象限；
（3）一次函数图象与二次函数图象的交点有_____个．

三、解答题
20．已知关于的方程.
(1)判断该方程是否有实数根？
(2)设此方程的两实数根为，，且，求的值．
21．如图，小明想要用撬棍撬动一块大石头，已知阻力为，阻力臂长为．设动力为，动力臂长为．（杠杆平衡时，动力×动力臂＝阻力×阻力臂，图中撬棍本身所受的重力略去不计）

(1)求关于的函数关系式（不要求写自变量的取值范围）；
(2)当动力臂长为时，撬动石头至少需要多大的力？
22．小明利用刚学过的测量知识来测量学校内一棵古树的高度.一天下午，他和学习小组的同学带着测量工具来到这棵古树前，由于有围栏保护，他们无法到达古树的底部B，如图所示.于是他们先在古树周围的空地上选择一点D，并在点D处安装了测量器CD，测得；再在BD的延长线上确定一点G，使米，并在G处的地面上水平放置了一个小平面镜，小明沿着BG方向移动，当移动到点F时，他刚好在小平面镜内看到这棵古树的顶端A的像，此时，测得米，小明眼睛与地面的距离米，测量器的高度米.已知点F、G、D、B在同一水平直线上，且EF、CD、AB均垂直于FB，则这棵古树的高度AB为多少米？（小平面镜的大小忽略不计）

23．某片果园有果树100棵，现准备多种一些果树提高果园产量，但是如果多种树，那么树之间的距离和每棵树所受光照就会减少，单棵树的产量随之降低．若该果园每棵果树产果y（千克），增种果树x（棵），它们之间的函数关系为：．
(1)在投入成本最低的情况下，增种果树多少棵时，果园可以收获果实8250千克？
(2)当增种果树多少棵时，果园的总产量w（千克）最大？最大产量是多少？
24．2022年虎年新春，中国女足逆转韩国，时隔16年再夺亚洲杯总冠军；2022年国庆，中国女篮高歌猛进，时隔28年再夺世界杯亚军，一扫男足、男篮颓势，展现了中国体育的风采！为了培养青少年人才储备，雅礼某初中开展了“阳光体育活动”，决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动，为了了解学生对这五项活动的喜爱情况，随机调查了一些学生（每名学生必选且只能选择这五项活动中的一种）．根据以下统计图提供的信息，请解答下列问题：

(1)本次被调查的学生有______名；补全条形统计图；
(2)扇形统计图中“排球”对应的扇形的圆心角度数是______；
(3)学校准备推荐甲、乙、丙、丁四名同学中的2名参加全市中学生篮球比赛，请用列表法或画树状图法分析甲和乙同学同时被选中的概率．
25．如图，抛物线与轴交于，两点，与轴交于点．

(1)求该抛物线的解析式；
(2)若点是抛物线的对称轴与直线的交点，点是抛物线的顶点，求的长．
26．如图，在△ABC中，∠ABC=90°，以AB的中点O为圆心、OA为半径的圆交AC于点D，E是BC的中点，连接DE，OE．

(1)判断DE与⊙O的位置关系，并说明理由；
(2)求证：BC2=CD·2OE；
(3)若AB：AC=3：5，BE=6，求OE的长．

参考答案：
1．B
【分析】直接从上往下看，看到的平面图形就是俯视图，据此作答即可．
【详解】根据题意，从上面看原图形可得到

故选：B．
【点睛】本题考查了简单组合体的三视图，熟练掌握知识点是解题的关键．
2．B
【分析】利用比例的性质，进行计算即可解答．
【详解】解：∵，
∴，
故选：B．
【点睛】本题考查了比例的性质，熟练掌握比例的性质是解题的关键．
3．A
【分析】按照“左加右减，上加下减”的规律进而求出即可．
【详解】解：将二次函数的图象向右平移个单位长度，再向下平移个单位长度得到的二次函数解析式是，即．
故选：A．
【点睛】此题考查了抛物线的平移以及抛物线解析式的变化规律：左加右减，上加下减．
4．D
【分析】直接利用正切的定义求解．
【详解】解：，
．
故选D．
【点睛】本题考查锐角三角函数的定义．熟练掌握正切等于对边比邻边是解题的关键．
5．D
【分析】根据反比例函数的性质直接解答即可．
【详解】解：将代入解析式，得，故A正确，不符合题意；
由于，则函数图象过一、三象限，在每个象限内，随的增大而减小，故B正确，不符合题意、D错误，符合题意；
∵时，，且当时，随的增大而减小
∴当时，，故C正确，不符合题意，
故选：D．
【点睛】本题考查了反比例函数的性质，解题的关键是掌握反比例函数的性质．
6．D
【分析】先根据求出，再根据相似三角形的判定方法解答．
【详解】∵，
∴，
A、添加，可用两角法判定，故本选项不符合题意；
B、添加，可用两角法判定，故本选项不符合题意；
C、添加，可用两边及其夹角法判定，故本选项不符合题意；
D、添加，不能判定，故本选项符合题意，
故选：D．
【点睛】本题考查了相似三角形的判定，先求出两三角形的一对相等的角是确定其他条件的关键，注意掌握相似三角形的几种判定方法．
7．A
【分析】根据事件发生的可能性大小判断相应事件的类型．
【详解】A、守株待兔是随机事件；
B、刻舟求剑是不可能事件；
C、水中捞月是不可能事件；
D、破镜重圆是不可能事件；
故选：A
【点睛】本题考查的是必然事件、不可能事件、随机事件的概念．必然事件指在一定条件下，一定发生的事件．不可能事件是指在一定条件下，一定不发生的事件，不确定事件即随机事件是指在一定条件下，可能发生也可能不发生的事件．
8．B
【分析】设所在圆的圆心为O，连接，，由垂径定理证明O、C、D三点共线，则，在中由勾股定理进行求解即可．
【详解】解：设所在圆的圆心为O，连接，，
∵C是的中点，
∴，
∵，
∴O、C、D三点共线，
∴，
∴，
在中由勾股定理得：，
∴，
∴，
故选B．

【点睛】本题主要考查了勾股定理和垂径定理，正确作出辅助线构造直角三角形是解题的关键．
9．C
【分析】连接．利用勾股定理求出，根据，计算即可．
【详解】连接．

四边形是平行四边形，
，
，
，
，
，
．
故选：C．
【点睛】本题考查扇形的面积的计算，平行四边形的性质，勾股定理等知识，解题的关键是掌握割补法求阴影部分的面积．
10．C
【分析】结合等边三角形的性质不难求得，则有，从而可求得，即可求得，则A正确；不难求得，则有，从而可判断B正确；只有当时，即，重合时，，，，此时，其它情况不成立，故C错误；首先证得，，，，从而得，故D正确．
【详解】解：和均为等边三角形，
，，
，
在和中，
，
，
，
，，，
，
，故A正确；
，，
，
，
，故B正确；
，，，
只有当时，即，重合时，，，此时，其它情况不成立，故C错误；
，
，
，
，
，
，，
，故D正确．
故选：C．
【点睛】本题考查相似三角形的判定，等边三角形的性质，解答的关键是结合图形分析清楚角与角，边与边之间的关系．
11．C
【分析】先求方程的根，可得r的值，由直线与圆的位置关系的判断方法可求解．
【详解】∵，
∴，，
∵的半径为一元二次方程的根，
∴，
∵，
∴直线l与的位置关系是相离，
故选：C．
【点睛】本题考查的是直线与圆的位置关系，解决此类问题可通过比较圆心到直线距离d与圆半径大小关系完成判定．
12．D
【分析】连接，如图所示，得到，再结合反比例函数的几何意义即可得到，解方程即可得到答案．
【详解】解：连接，如图所示：

轴，
，
，
，解得，
故选：D．
【点睛】本题考查反比例函数的几何意义，读懂题意，数形结合是解决问题的关键．
13．A
【分析】如图所示，根据题意可知，得到相似比，从而根据在时测得某树的影长为，时又测得该树的影长为，代入值求解即可得到树的高度为，从而得到答案．
【详解】解：如图所示：

，
，
，
，
，
，
，
，
，
，解得，
树的高度为，
故选：A．
【点睛】本题考查利用相似三角形解实际应用题，读懂题意，看懂图形，准确得到相似三角形及相似比是解决问题的关键．
14．C
【分析】根据二次函数的图象逐项判断即可；
【详解】解：由图可知，抛物线的对称轴为
∴
整理得： ，故①错误；
当 时， ；故②正确；
∵该抛物线的对称轴为
∴根据抛物线的对称性可知，该二次函数的图象与轴相交于
∴关于的方程的两个解是，；故③正确；
由图象可知，当时，随的增大而减小；故④正确；
故选：C．
【点睛】本题考查了二次函数图象的性质；熟练掌握二次函数图象的性质是解题的关键．
15．B
【分析】根据切于点A，得到，再由，根据直角三角形中两锐角互余即可得到，由中，利用等腰三角形性质即可得到，从而得到答案．
【详解】解：切于点，
，即，
在中，，，
则，
在中，
，
故选：B．
【点睛】本题考查切线的性质，直角三角形性质，圆的性质及等腰三角形的判定与性质，熟练掌握相关几何性质是解决问题的关键．
16．C
【分析】列表得出所有等可能结果，从中找到符合条件的结果数，再根据概率公式求解即可．
【详解】解：将“立春”、“立夏”、“秋分”、“大暑”的图片分别记为A、B、C、D．根据题意，列表如下：

A
B
C
D
A

（A，B）
（A，C）
（A，D）
B
（B，A）

（B，C）
（B，D）
C
（C，A）
（C，B）

（C，D）
D
（D，A）
（D，B）
（D，C）


由表格可知，共有12种等可能的结果，其中抽到的两张卡片恰好是“立春”和“立夏”的结果有2种，
故其概率为：．
故选：C．
【点睛】本题考查了列表法与树状图法：利用列表法或树状图法展示所有等可能的结果n，再从中选出符合事件A或B的结果数目m，然后利用概率公式计算事件A或事件B的概率．
17．12
【分析】行和频率估计 出概率，然后设木箱中蓝色卡片x个，根据概率公式列出算式，再进行计算即可得出答案．
【详解】解：设木箱中蓝色卡片有x个，根据题意得：
，
解得：，
经检验是原方程的解，
则估计木箱中蓝色卡片有12张．
故答案为：12．
【点睛】本题利用了用大量试验得到的频率可以估计事件的概率，概率公式，关键是根据蓝色卡片的频率得到相应的等量关系．
18．     ∠BAD    
【分析】(1) 根据△ABC是等边三角形,得到∠B=∠C= 60°， AB= BC；又因为∠ADC=∠B+∠BAD，∠EDC+∠ADE= ∠B+∠BAD就得到∠EDC=∠BAD
(2) 因为∠EDC=∠BAD，∠C=∠B得到△ABD~△DCE，得到 ，即可求出EC；
【详解】(1) 证明: ∵△ABC是等边三角形,
∠B=∠C= 60°， AB= BC；
又∵∠ADC=∠B+∠BAD
∠EDC+∠ADE= ∠B+∠BAD
又∵∠ADE=∠B=60°
∴∠EDC=∠BAD
所以和∠CDE相等的角为：∠BAD
故答案为：∠BAD
(2) ∵∠EDC=∠BAD
∴∠C=∠B
△ABD~△DCE，


又

解得：EC=
故答案为： ；
【点睛】此题主要考查了等边三角形的性质和相似三角形的判定和性质，能够证得△ABD~△DCE是解答此题的关键．
19．     减小     四     2
【分析】（1）由直线y＝ax+b经过第一、三、四象限可得a＞0，b＜0，从而可得抛物线开口方向及对称轴位置，进而求解．
（2）由a＞0，b＜0可得抛物线与x轴由两个交点，从而可得顶点位置．
（3）联立直线与抛物线方程，根据判别式的符号判断交点个数．
【详解】解：（1）∵直线y＝ax+b经过第一、三、四象限，
∴a＞0，b＜0，
∴抛物线y＝a+bx﹣2开口向上，
∵﹣＞0，
∴x＜0时，y随x增大而减小，
故答案为：减小．
（2）∵a＞0，b＜0，
∴Δ＝+8a＞0，
∴抛物线与x轴有两个交点，即抛物线顶点在x轴下方，
∴抛物线顶点在第四象限，
故答案为：四．
（3）令a+bx﹣2＝ax+b，
整理得a+（b﹣a）x﹣2﹣b＝0，
∴Δ＝+4a（2+b）＝﹣2ab+ +4ab+8a＝+8a＞0，
∴一次函数图象与二次函数图象的交点有2个，
故答案为：2．
【点睛】本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系，掌握二次函数与方程的关系．
20．(1)原方程有实数根；
(2)

【分析】（1）利用一元二次方程根的判别式即可判断；
（2）先根据公式法求出和的值，再建立关于的方程进行求解，即可得到的值．
【详解】（1）解：，
原方程有实数根；
（2）解：由（1）知，，
，
，为方程的两个实数根，
，，
，
，解得，
经检验：是原方程的解．
【点睛】本题考查了一元二次方程根的判别式，公式法解一元二次方程，熟练掌握一元二次方程额相关知识是解题关键．
21．(1)关于的函数关系式为
(2)当动力臂长为时，撬动石头至少需要的力

【分析】（1）根据题意，杠杆平衡时，动力×动力臂＝阻力×阻力臂，代值求解即可得到关于的函数关系式；
（2）由（1）中得到的函数表达式，当动力臂长为时，即时求函数值即可得到答案．
【详解】（1）解：由题意得，
，
即关于的函数关系式为；
（2）解：∵，
∴当时，，
即当动力臂长为时，撬动石头至少需要的力．
【点睛】本题考查反比例函数解实际应用题，读懂题意，得到反比例函数表达式是解决问题的关键．
22．
【分析】过点作于点，则，，解，得出，那么，再证明，因此得出，再求出即可.
【详解】如图，过点作于点，则，，
在中，，

∴，
∴，
∵，，
∴
由反射角等于入射角得,
∴,
∴，即，
解得
∴
∴这棵树高18米.
【点睛】本题主要考查相似三角形的应用，证明三角形相似是解题的关键.
23．(1)增种果树10棵时，果园可以收获果实8250千克．
(2)当增种果树30棵时果园的总产量w（千克）最大，最大产量是8450千克．

【分析】（1）列出方程解方程，再根据实际意义确定x的值．
（2）构建二次函数，利用二次函数性质解决问题．
【详解】（1）根据题意，得：，
解得，
∵投入成本最低．
∴不满足题意，舍去．
∴增种果树10棵时，果园可以收获果实8250千克．
（2）根据题意，得：



∵，则抛物线开口向下，函数有最大值
∴当时，w最大值为8450千克．
∴当增种果树30棵时果园的最大产量是8450千克．
【点睛】本题考查二次函数的应用、一元二次方程等知识，解题的关键是熟练掌握待定系数法，学会构建二次函数解决实际问题中的最值问题，属于中考常考题型．
24．(1)100；图见解析
(2)
(3)

【分析】（1）喜爱篮球的学生人数与所占百分比的比值即为被调查的学生人数，然后根据喜爱足球所占百分比计算出喜爱足球学生人数，然后补全条形统计图；
（2）先计算出喜爱排球的学生百分比，再与相乘即可；
（3）画出树状图，计算甲和乙同学同时被选中的结果数与所有情况数的比值即可．
【详解】（1）解：本次被调查的学生人数为（名）．
故答案为：100．
选择“足球”的人数为（名）．
补全条形统计图如下：

（2）解：扇形统计图中“排球”对应的扇形的圆心角度数为．
故答案为：18°．
（3）解：画树状图如下：

共有12种等可能的结果，其中甲和乙同学同时被选中的结果有2种，
∴甲和乙同学同时被选中的概率为．
【点睛】本题考查了条形统计图与扇形统计图关联、求扇形统计图圆心角、树状图或列表法求概率，熟练结合条形统计图和扇形统计图综合分析是解题关键．
25．(1)该抛物线的解析式为
(2)

【分析】（1）根据题意，利用待定系数法求抛物线表达式，将，代人得，解二元一次方程组即可得到答案；
（2）将（1）中抛物线化为顶点式，得到抛物线的顶点的坐标为，抛物线的对称轴为直线，利用待定系数法求出直线的解析式，进而得到点的坐标为，根据点的坐标特征即可求出的长．
【详解】（1）解：将，代人，得
，解得，
∴该抛物线的解析式为；
（2）解：∵抛物线的解析式为，
∴抛物线的顶点的坐标为，抛物线的对称轴为直线，
当时，，
∴点的坐标为，
设直线的解析式为（），将，代人，得，解得，
∴直线的解析式为，
抛物线的对称轴与直线的交点为，
当时，，即点的坐标为，
∴．
【点睛】本题考查二次函数与一次函数综合，涉及待定系数法求二次函数解析式、待定系数法求一次函数解析式、一般式化为顶点式、求抛物线与坐标轴交点等知识，数形结合求出抛物线及直线的解析式是解决问题的关键．
26．(1)DE为⊙O的切线，理由见解析
(2)见解析
(3)OE=

【分析】（1）连接OD，BD，根据直径所对的圆周角是直角得到∠ADB=90°，再由直角三角形斜边上的中线等于斜边的一半得到CE=DE=BE=BC，推出∠C=∠CDE，再证明∠A=∠ADO，根据∠C+∠A=90°，得到∠ADO+∠CDE=90°，即∠ODE=90°，即可证明结论；
（2）先由三角形中位线定理得到AC=2OE，再证明△ABC∽△BDC，得到 ，即,即可证明；
（3）设AB=3k，AC=5k，在Rt△ABC中，，即，由此求解k的值即可得到答案．
【详解】（1）解：DE与⊙O相切，理由如下：
连接OD，BD，
∵AB为圆O的直径，
∴∠ADB=90°，
在Rt△BDC中，E为斜边BC的中点，
∴CE=DE=BE=BC，
∴∠C=∠CDE，
∵OA=OD，
∴∠A=∠ADO，
∵∠ABC=90°，即∠C+∠A=90°，
∴∠ADO+∠CDE=90°，即∠ODE=90°，
∴DE⊥OD，又OD为圆的半径，
∴DE为⊙O的切线；

（2）解：∵E是BC的中点，O点是AB的中点，
∴OE是△ABC的中位线，
∴AC=2OE，
∵∠C=∠C，∠ABC=∠BDC，
∴△ABC∽△BDC，
∴ ，即,
∴；
（3）解：∵BE=6，E是BC的中点，即BC=12，
∵AB：AC=3：5,
设AB=3k，AC=5k，在Rt△ABC中，，
∴，
解得k=3，
∴AC=15，
又∵AC=2OE，
∴．
【点睛】本题主要考查了圆切线的判定，等腰三角形的性质与判定，直角三角形斜边上的中线，三角形中位线定理，勾股定理，直角三角形两锐角互余，相似三角形的性质与判定，直径所对的圆周角是直角等等，正确作出辅助线是解题的关键．