吉林省长春外国语学校2022-2023学年七年级上学期期末考试数学试题

这是一份吉林省长春外国语学校2022-2023学年七年级上学期期末考试数学试题，共18页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
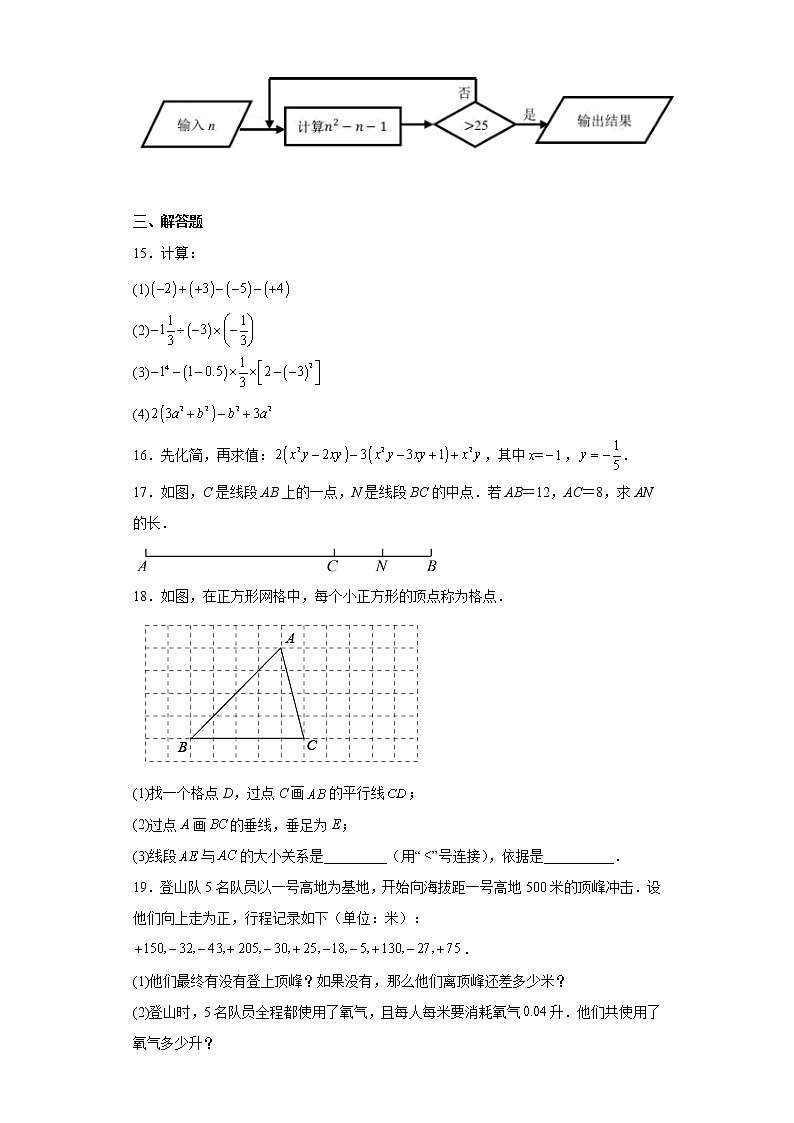
吉林省长春外国语学校2022-2023学年七年级上学期期末考试数学试题学校:___________姓名：___________班级：___________考号：___________ 一、单选题1．的相反数是（    ）A．2 B． C． D．2．在，2.3，0，四个数中，最大的数是（    ）A． B．2.3 C．0 D．3．下列选项中，两数相等的是（    ）A．与 B．与C．与 D．与4．如果a-3b=4，那么2a-6b-1的值是（    ）A．-7 B．5 C．7 D．-55．这是一个小正方体的展开图，把展开图折叠成小正方体后，有“喜”字一面的相对面上的字是（    ）A．百 B．迎 C．年 D．党6．如图所示，由A到B有①、②、③三条路线，最短的路线选①的理由是（       ）A．两点确定一条直线 B．两点间距离的定义C．两点之间，线段最短 D．因为它直7．如图所示，，点，，在同一直线上．若，则的度数为（）A． B． C． D．8．如图，A，B两地之间有一条东西向的笔直道路．在A地的正东方向处设置第一个广告牌，之后每往东就设置一个广告牌．一辆汽车在A地的正西方向处出发，沿此路自西向东行驶，当经过第n个广告牌时，此车所行驶的路程为（    ）A． B． C． D． 二、填空题9．比较大小： ______10．今年全国粮食总产量亿斤，比上年增加亿斤，亿用科学计数法可以表示___________．11．已知与的和仍是单项式，则的值是___________．12．如果，那么它的补角等于_________．13．如图，把一块长方形纸条沿折叠，若，那么____________．14．如图，这是一个简单的数值运算程序，当输入的值为3时，输出的结果为___________． 三、解答题15．计算：(1)(2)(3)(4)16．先化简，再求值：，其中，．17．如图，C是线段AB上的一点，N是线段BC的中点．若AB＝12，AC＝8，求AN的长．18．如图，在正方形网格中，每个小正方形的顶点称为格点．(1)找一个格点D，过点C画的平行线；(2)过点A画的垂线，垂足为E；(3)线段与的大小关系是_________（用“”号连接），依据是__________．19．登山队5名队员以一号高地为基地，开始向海拔距一号高地500米的顶峰冲击．设他们向上走为正，行程记录如下（单位：米）：．(1)他们最终有没有登上顶峰？如果没有，那么他们离顶峰还差多少米？(2)登山时，5名队员全程都使用了氧气，且每人每米要消耗氧气升．他们共使用了氧气多少升？20．如图，直线和相交于点O，，平分，．(1)求的度数；(2)求的度数．21．填空并在括号内加注理由．如图，已知，，垂足分别为D、F，，试说明：．请补充说明过程，并在括号内填上相应的理由．解：∵，（已知）∴（___________）∴___________（___________）又∵（已知），∴（___________）∴___________（___________）∴（___________）22．第24届冬季奥林匹克运动会于2022年2月4日至2022年2月20日在北京市和张家口市联合举行，北京是唯一个既举办冬季奥运会又举办夏季奥运会的城市．为了迎北京冬季奥运会，我校准备举行冬季长跑比赛，为奖励长跑优胜者，学校需要购买冰墩墩水杯和雪容融徽章共50件．现了解到某商店水杯单价28元，徽章单价16元，设水杯买个．(1)学校一共需要支付_____________元．（用含a的代数式表示）(2)该商店推出两种优惠方案，方案一：消费额超过200元的部分打八折；方案二：全店商品打九折．若学校需要购买10个水杯，选择哪种方案更优惠？说明理由．23．课题学习：平行线问题中的“转化思想”[阅读理解]“两条平行线被第三条直线所截”是平行线中的一个重要的“基本图形”，所有的与平行线有关的角都存在于这个“基本图形”中，且都分布在“第三条直线”的两旁，当发现题目的图形“不完整”时，要通过适当的辅助线将其补完整．将“非基本图形”转化为“基本图形”．在“相交线与平行线”的学习中，有这样一道典型问题：例题如图①，已知，若，，则有_____________°．分析：从图形上看，由于没有一条直线截与，所以无法直接运用平行线的相关性质，这就需要构造出“两条平行线被第三条直线所截"基本图形后，才可以运用平行线的条件或性质．过E点作，根据平行于第三条直线的两直线平行，可得，这样可将图形转化，进而可以求出．[方法应用]已知，（1）如图②，若，，求的度数；（2）如图②，直接写出、、之间的数量关系；（3）如图③，平分，平分，，则的度数为______________．24．如图①，点C在线段上，图中共有3条线段：和，若其中有一条线段的长度是另一条线段长度的两倍，则称点C是线段的“巧点”．(1)①一条线段的中点__________这条线段的“巧点”；（填“是”或“不是”）②若线段，C是线段的“巧点”，则_________．（用含m的代数式表示出所有可能的结果）(2)如图②， A、B为数轴上两点，点A所表示的数为，点B所表示的数为20．动点P从点A出发，以每秒的速度沿向终点B匀速移动．点Q从点B出发，以每秒的速度沿向终点A匀速移动，点P，Q同时出发，当其中一点到达终点时运动停止，若设移动的时间为t秒，求当t为何值时，点Q恰好是线段的“巧点”．
参考答案：1．B【分析】直接根据相反数定义解答即可．【详解】解：的相反数是．故选B．【点睛】本题主要考查了相反数的定义，掌握相反数的概念成为解答本题的关键．2．B【分析】根据有理数大小比较方法进行比较即可．【详解】解：根据正数大于0，0大于负数可以判断，2.3最大；故选：B．【点睛】本题考查了有理数大小的比较，解题关键是掌握有理数比较大小的法则，准确判断．3．B【分析】根据有理数的乘方运算法则、绝对值化简和相反数，逐一计算即可得到答案．【详解】解：A、，，两数不相等，不符合题意，选项错误；B、，，两数相等，符合题意，选项正确；C、，，两数不相等，不符合题意，选项错误；D、，，两数不相等，不符合题意，选项错误，故选B．【点睛】本题考查了有理数的乘方，绝对值，相反数，熟练掌握相关运算法则是解题关键．4．C【分析】将整体代入即可求解．【详解】∵，∴，故选：C．【点睛】本题考查了已知式子的值求代数式的值的知识，将整体代入是解答本题的关键．5．D【分析】根据相对的面之间一定相隔一个正方形解答，即可．【详解】解：正方体的表面展开图，相对的面之间一定相隔一个正方体，“喜”与“党”是相对面． 故选：D．【点睛】本题主要考查了正方体相对两个面上的文字，注意正方体的空间图形，从相对面入手，分析及解答问题．6．C【分析】根据基本事实：两点之间，线段最短，直接作答即可.【详解】解：由A到B有①、②、③三条路线，最短的路线选①的理由是：两点之间，线段最短.故选C【点睛】本题考查的是两点之间，线段最短的实际应用，掌握“几何基本事实或图形的性质在生活中的应用”是解本题的关键.7．A【分析】由图示可得，与互余，结合已知可求，又因为与互补，即可求出的度数．【详解】，，，点，，在同一直线上，，．故选：A．【点睛】此题考查了余角和补角的知识，属于基础题，关键是掌握互余的两角之和为，互补的两角之和为．8．A【分析】根据题意和图形，可以用代数式表示出这辆汽车行驶的路程，本题得以解决．【详解】解：由题意可得，一汽车在A地的西处出发，沿此道路向东行驶．当经过第n个广告牌时，此车所行驶的路程为：，故选A．【点睛】本题考查列代数式，解答本题的关键是明确题意，列出相应的代数式，利用数形结合的思想解答．9．＜【分析】直接根据正数大于0，负数小于0，负数的绝对值越大，这个数越小判断即可．【详解】解： =，=，∵＞，∴＜，∴＜，故答案为：＜．【点睛】本题考查了有理数大小比较：正数大于0，负数小于0；负数的绝对值越大，这个数越小．10．【分析】根据科学记数法表示即可．【详解】解：∵亿，∴，故答案为：．【点睛】本题考查了科学记数法，灵活运用所学知识求解是解决本题的关键．11．####6.5【分析】根据和仍是单项式是同类项可得，求出m，n的值，然后代入求值即可．【详解】解：由题意可得和是同类项,∴，解得：，∴故答案为：．【点睛】本题考查了同类项，代数式求值．解题的关键在于求解m，n的值．12．【分析】根据互补角的定义、角的运算法则即可得．【详解】∵，∴的补角等于，故答案为：．【点睛】本题考查了互补角的定义（同一平面内的两个角相加的和等于180度）、角的运算法则，掌握理解互补角的定义是解题关键．13．116 【分析】根据长方形的对边平行知AD∥BC，据此得，再根据折叠变换的性质知，继而由可得答案．【详解】解：由题意知，∴，根据折叠变换的性质知，则，∴故答案为：116．【点睛】本题主要考查平行线的性质，解题的关键是掌握两直线平行内错角相等的性质、翻折变换的性质．14．341【分析】将代入数值运算程序计算，判断结果与25大小，小于或等于25再代入计算，大于25输出，即可得到输出结果．【详解】解：当时，根据数值运算程序得：，当时，根据数值运算程序得：，当时，根据数值运算程序得：，则输出结果为341．故答案为：341【点睛】此题考查了代数式求值，熟练掌握运算法则是解本题的关键．15．(1)2(2)(3)(4) 【分析】（1）根据有理数的加减法混合运算求解即可；（2）根据有理数的乘除法混合运算求解即可；（3）根据含乘方的有理数的混合运算求解即可；（4）根据整式的加减法混合运算求解即可；【详解】（1）解：；（2）解：；（3）解：；（4）解：．【点睛】本题考查了整式的加减混合运算和有理数的混合运算，正确的计算是解决本题的关键．16．，【分析】原式去括号，合并同类项进行化简，然后代入求值．【详解】解：，当，时，原式．【点睛】本题考查了整式的加减—化简求值，熟练掌握运算法则是解题的关键．17．10【分析】先根据已知求出BC的长，再根据N是线段BC的中点求出CN，从而求出AN．【详解】解：∵AB＝12，AC＝8，∴BC＝AB﹣AC＝12﹣8＝4，∵N是线段BC的中点，∴CN＝BC＝×4＝2，∴AN＝AC＋CN＝8＋2＝10．【点睛】本题考查的是两点间的距离，熟知各线段之间的和、差及中点的性质是解答此题的关键．18．(1)见解析(2)见解析(3)，垂线段最短 【分析】（1）根据网格结构特点，可过点C画的平行线；（2）根据网格结构特点作出即可；（3）根据垂线段最短可得答案．【详解】（1）解：如图，即为所求；（2）解：如图，即为所求；（3）解：根据是垂线段最短得：线段与的大小关系是，故答案为：，垂线段最短．【点睛】本题考查作图——应用与设计作图，掌握利用网格结构作垂线，平行线是解题的关键．19．(1)他们没能最终登上顶峰，离顶峰还有70米(2)他们共使用了氧气148升 【分析】（1）约定前进为正，后退为负，依题意列式求出和，再与500比较即可；（2）要消耗的氧气，需求他共走了多少路程，这与方向无关．【详解】（1）根据题意得：总共爬了米，米．∴他们没能最终登上顶峰，离顶峰还有70米；（2）根据题意得：米，升．∴他们共使用了氧气148升．【点睛】此题不但考查了正数和负数在实际生活中的应用，而且用到了有理数的加法，需同学们熟练掌握．20．(1)的度数为(2)的度数为 【分析】（1）首先根据题意计算出，再利用邻补角之和等于计算即可；（2）根据角平分线的定义求出的度数，再由计算即可．【详解】（1）∵，，∴，，∴；（2）∵平分，∴，∴．【点睛】本题主要考查了平角、邻补角以及角平分线的定义（从一个角的顶点引出一条射线，把这个角分成两个完全相同的角，这条射线叫做这个角的角平分线），解题关键是弄清题意，确定各角之间的关系．21．同位角相等，两直线平行；；两直线平行，同旁内角互补；同角的补角相等；；内错角相等，两直线平行；两直线平行，同位角相等【分析】根据平行线的判定与性质即可求解．【详解】解：∵，（已知），∴（同位角相等，两直线平行）∴（两直线平行，同旁内角互补）又∵（已知），∴（同角的补角相等）∴（内错角相等，两直线平行）∴（两直线平行，同位角相等）．故答案为：同位角相等，两直线平行；；两直线平行，同旁内角互补；同角的补角相等；；内错角相等，两直线平行；两直线平行，同位角相等．【点睛】本题考查平行线的判定和性质，解题的关键是熟掌握平行线的性质与判定．22．(1)(2)方案一更优惠，理由见解析 【分析】（1）设水杯买个，则徽章买个，根据“水杯单价28元，徽章单价16元，”列出代数式，即可；（2）根据方案一与方案二进行计算，比较结果即可得出那个方案更优惠．【详解】（1）解：设水杯买个，则徽章买个，∴学校一共需要支付元；故答案为：（2）解：方案一更优惠，理由如下：根据题意得：学校需要购买个徽章，方案一：，元；方案二：元，∵，∴方案一更优惠．【点睛】本题主要考查了列代数式，整式的加减的应用，有理数的混合运算的应用，明确题意，准确列出代数式是解题的关键．23．（1）；（2）；（3）【分析】（1）过点E作，可得，从而得到，即可求解；（2）过点E作，可得，从而得到，即可求解；（3）过点F作，可得，从而得到，则两式相加可得，再由平分，平分，可得，进而得到，由（2）知，，即可求得结果．【详解】解：（1）如图，过点E作，∵，∴，∵，∴，∴；（2）如图，过点E作，∵，∴，∴，∴；（3）如图，过点F作，∵，∴，，即，，平分，平分，， ，或，由（2）知，，．【点睛】本题主要考查了平行线的判定和性质，熟练掌握平行线的判定和性质是解题的关键．难点是作辅助线——平行线．24．(1)①是；②或或(2)10或或或15或或 【分析】（1）①由中点可知这条线段的长度等于中点分出的线段长度的2倍，结合“二倍点”的定义进行判断；②由“二倍点”的定义知当点C是线段的“二倍点”时，可分，，三种情况，根据 计算，即可求解；（2）由题意知，然后分两类讨论：当点P在点Q的左侧时，当点P在点Q的右侧时，结合“巧点”的定义，求解即可．【详解】（1）解∶ ① 根据题意得：这条线段的长度等于中点分出的线段长度的2倍，∴一条线段的中点是这条线段的“巧点”；故答案为：是②线段，C是线段的“巧点”，∴当时，；当时，；当时，；综上所述，或或；故答案为：或或（2）解∶∵点A所表示的数为，点B所表示的数为20，∴，根据题意得：点P所对应的数为，点Q所对应的数为，当时，点P，Q相遇，当点P在点Q的左侧时，，，此时，若，则有，解得：；若，则有，解得：；若，则有，解得：；当点P在点Q的右侧时，，，此时，若，则有，解得：；若，则有，解得：；若，则有，解得：；综上所述，当t为10或或或15或或时，点Q恰好是线段的“巧点”．【点睛】本题主要考查了一元一次方程的应用，线段间的数量关系，利用分类讨论思想解答是解题的关键．