

2022-2023学年重庆市沙坪坝区南开中学八年级(上)期末数学试卷
展开2022-2023学年重庆市沙坪坝区南开中学八年级(上)期末数学试卷
一、选择题(本大题共12个小题,每小题4分,共48分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将正确答案在答题纸中对应位置涂黑.
1.下列各数中,无理数是( )
A. B.2 C. D.0.0101
2.已知点(﹣1,y1),(3,y2)在一次函数y=2x+1的图象上,则y1,y2的大小关系是( )
A.y1<y2 B.y1=y2 C.y1>y2 D.不能确定
3.已知x<y,则下列不等式一定成立的是( )
A.x﹣5>y﹣5 B.﹣2x>﹣2y C.a2x<a2y D.
4.在数轴上表示不等式组的解集,正确的是( )
A. B.
C. D.
5.的整数部分为( )
A.2 B.3 C.4 D.5
6.将多项式x3﹣2x2+x因式分解正确的是( )
A.x(x2﹣2x) B.x(x2﹣2x+1) C.x(x+1)2 D.x(x﹣1)2
7.直线l1:y=kx﹣b和直线l2:yx+2b在同一坐标系中的图象大致是( )
A. B.
C. D.
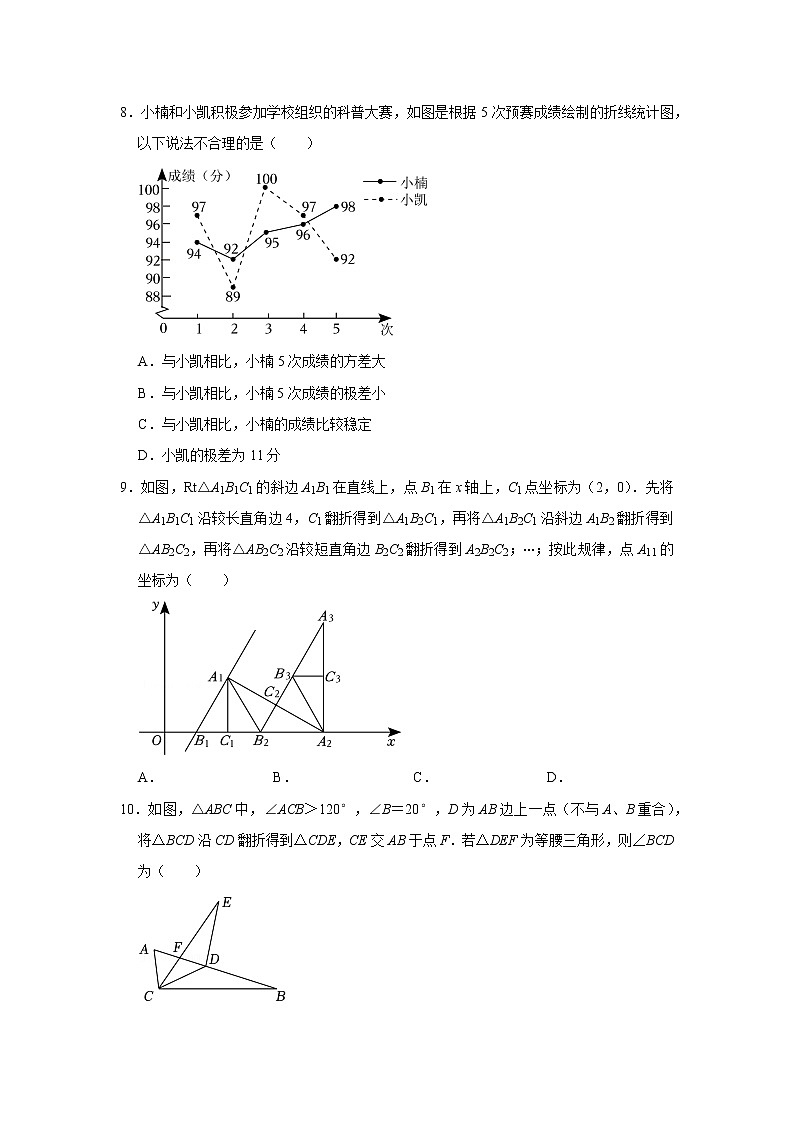
8.小楠和小凯积极参加学校组织的科普大赛,如图是根据5次预赛成绩绘制的折线统计图,以下说法不合理的是( )
A.与小凯相比,小楠5次成绩的方差大
B.与小凯相比,小楠5次成绩的极差小
C.与小凯相比,小楠的成绩比较稳定
D.小凯的极差为11分
9.如图,Rt△A1B1C1的斜边A1B1在直线上,点B1在x轴上,C1点坐标为(2,0).先将△A1B1C1沿较长直角边4,C1翻折得到△A1B2C1,再将△A1B2C1沿斜边A1B2翻折得到△AB2C2,再将△AB2C2沿较短直角边B2C2翻折得到A2B2C2;⋯;按此规律,点A11的坐标为( )
A. B. C. D.
10.如图,△ABC中,∠ACB>120°,∠B=20°,D为AB边上一点(不与A、B重合),将△BCD沿CD翻折得到△CDE,CE交AB于点F.若△DEF为等腰三角形,则∠BCD为( )
A.30° B.30°或60° C.50° D.30°或50°
11.若关于x的不等式组有解且至多有3个整数解,且多项式x2﹣(3m+1)能在有理数范围内因式分解,则符合条件的整数m的个数为( )
A.0 B.1 C.2 D.3
12.关于x的新函数定义如下:
(1)当x=0时,y=1:
(2)当(p是正整数,q是整数,q≠0,且p,q不含除1以外的公因数)时,;
(3)当x为无理数时,y=0.
例:当x时,y当x时,y.
以下结论:①当x时,y=0;
②若a、b是互不相等且不为0的有理数,当x=a时,函数值记为y1,当x=b时,函数值记为y2,当x=a•b时,函数值记为y3,则一定有y1y2=y3:
③若,则对应的自变量x有且只有4种不同的取值;
④若2022≤x≤2023,则满足的自变量x的取值共有12个.
正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二、填空题:(本大题共10个小题,每小题3分,共30分)请将每小题的答案直接填在答题纸中对应的横线上。
13.9的算术平方根是 .
14.若代数式有意义,则x的取值范围是 .
15.点A(﹣4,2)关于y轴的对称点的坐标为 .
16.已知一次函数y=(k2+1)x﹣1和y=﹣x+5相交于点A(2,a),则不等式﹣x+5<(k2+1)x﹣1中x的取值范围为 .
17.如图:化简 .
18.已知xy=1,3y﹣x=3,则3xy2﹣x2y﹣xy的值为 .
19.不等式ax+b>0的解集为,则关于x的不等式bx<a的解集为 .
20.如图,一个长方体盒子,其中AB=9,BC=3,M为AB上靠近A的三等分点,在大长方体盒子上有一个小长方体盒子,EC=6,CG=1,CF=4,一只蚂蚁要沿着长方体盒子的表面从点M爬行到N点,它爬行的最短路程为 .
21.如图,点D为等边△ABC外一点,连结DA,DC,BD.若AD=2,AC=2,∠ADC=120°,则BD= .
22.甲、乙、丙、丁是四个不同平台的外卖员,每配送一单即可获得相应配送费且均为整数.已知乙每一单的配送费为甲的两倍,丁每一单的配送费为丙的两倍.12月第一周,甲、乙、丙的配送量之比为4:6:5,丁的配送量为100单,且他们共获得配送费3700元.第二周配送量增加,甲增加的配送量占乙、丙配送量之和的32%,丙增加的配送量占甲、乙、丙增加的配送量之和的,此时甲、乙的配送量之和为丙的配送量的倍,丁的配送量增加60单,且他们共获得配送费7660元.若丁每单配送费高于4元且不超过8元,则第二周四位外卖员配送量之和为 单.
三、计算题:(本大题共2个小题,每小题8分,共16分)解答时给出必要的演算过程,请将解答过程书
23.(1)计算:(π﹣2)0;
(2)因式分解:(2m﹣n)2﹣(m﹣2n)2.
24.解下列不等式(组):
(1)10﹣5(2x﹣1)≥3﹣x;
(2).
四、解答题:(本大题共6个小题,25题~26题每小题8分,27题~30题每小题8分,共56分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题纸中对应的位置上.
25.请根据函数相关知识,对函数y=|x+1|的图象与性质进行探究,并解决相关问题:
①列表:
x | … | ﹣4 | ﹣3 | ﹣2 | n | 0 | 1 | 2 | … |
y | … | m | 2 | 1 | 0 | 1 | 2 | 3 | … |
②描点;③连线.
(1)表格中,m= .n= ;
(2)如图,在平面直角坐标系xoy中,画出函数y=|x+1|图象:根据图象,写出函数的一条性质: ;
(3)函数y=|x+1|的图象与函数yx+1的图象围成的三角形的面积为 .
26.如图,在△ABC中,过点A作AD⊥BC于点D,点E在线段BD上,且EA=EB.已知BD=16,AD=12,AC=15.
(1)求线段DE的长;
(2)求证:∠BAC=90°.
27.为了解学生线上学习期间居家劳动的开展情况,北关中学对该校1200名七年级学生和1500名八年级学生的平均每天居家劳动时间进行了调查,现从中各随机抽取20名学生的平均每天居家劳动时间t(min)进行整理、描述和分析,下面给出了部分信息.
七年级20名学生的平均每天居家劳动时间为:
30,30,35,40,40,40,40,40,40,40,40,45,45,50,55,55,55,60,60,60.
八年级20名学生的平均每天居家劳动时间的统计图如下:
七、八年级抽取的学生的平均每天居家劳动时间的平均数、众数、中位数如表所示:
年级 | 平均数 | 众数 | 中位数 |
七年级 | 45 | a | 40 |
八年级 | 45 | 45 | b |
根据以上信息,解答下列问题:
(1)m= ,a= ,b= ;
(2)如果学校要从中选取一个年级进行居家劳动活动的经验和心得分享,根据以上数据,你认为选择哪个
年级较好?请说明理由(写出一条理由即可);
(3)平均每天居家劳动时间大于或等于50min的学生会被授予“劳动达人”的称号,请估计此次七、八年
级的学生被授予此称号的人数共有多少?
28.农历新年初一吃汤圆,象征幸福团圆.某超市为迎接即将到来的春节,准备购进A、B两种汤圆.已知每袋A汤圆的成本比每袋B汤圆的成本贵5元,且购进3袋A汤圆与购进4袋B汤圆的成本相同.
(1)A、B两种汤圆每袋的成本分别为多少元?
(2)该超市决定采购A、B两种汤圆共180袋,要求购进A汤圆的数量不少于46袋且为偶数,采购A、B两种汤圆投入的资金不超过2960元.为促销两种汤圆,将两袋A汤圆捆绑销售,购买两袋A汤圆后加10元换购一袋B汤圆.已知A汤圆售价为28元/袋,B汤圆售价为20元/袋,且购买两袋A汤圆的顾客一定会换购一袋B汤圆,则超市应该如何进货,才能使得全部售完后利润最大?最大利润为多少?
29.如图,直线l1:y=2x+6交x轴、y轴分别于点A、B,直线l2:y=kx+b与直线l交于点D,与x轴交于点C.已知C(3,0),D点的横坐标为﹣1.
(1)求直线l2的解析表达式.
(2)若E在线段AC上,四边形BDEC的面积为14,求E点坐标.
(3)若点M、N分别为直线l1、l2上的动点,连结OM、ON、MN,当△OMN是以OM为直角边的等腰直角三角形时,请直接写出所有点M的坐标,并把求其中一个点M的坐标过程写出来.
30.如图1,在等腰△ABC中,AB=AC,点D是△ABC外一点,点P在射线CD上,其关于线段AD的对称点Q刚好落在线段BD上.
(1)求证:∠ABD=∠ACD;
(2)如图2,连结PQ,交AD于E点,若AD=PD,请探索BD、CD、DE之间的数量关系,并证明;
(3)如图3,在(2)的条件下,线段BD与AC交于点M(M在线段AC上),在线段CB上取点N,使得CN=AM.已知∠BAC=90°,AB=1,当AN+BM的值最小时,请直接写出△ENQ的面积.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布日期:2023/1/25 17:27:24;用户:单静怡;邮箱:zhaoxia39@xyh.com;学号:39428212
2023-2024学年重庆市沙坪坝区南开中学九年级(上)期中数学试卷: 这是一份2023-2024学年重庆市沙坪坝区南开中学九年级(上)期中数学试卷,共38页。试卷主要包含了选择题.,填空题,解答题等内容,欢迎下载使用。
2022-2023学年重庆市沙坪坝区南开中学七年级(下)开学数学试卷(含解析): 这是一份2022-2023学年重庆市沙坪坝区南开中学七年级(下)开学数学试卷(含解析),共24页。试卷主要包含了选择题,填空题,解答题等内容,欢迎下载使用。
2022-2023学年重庆市沙坪坝区南开中学八年级(下)入学数学试卷(含答案): 这是一份2022-2023学年重庆市沙坪坝区南开中学八年级(下)入学数学试卷(含答案),共21页。试卷主要包含了填空题,解答题等内容,欢迎下载使用。












