河南省南阳市桐柏县2022-2023学年八年级上学期期末数学试题(含答案)

这是一份河南省南阳市桐柏县2022-2023学年八年级上学期期末数学试题(含答案)，共10页。试卷主要包含了答题前填写好自己的姓名，请将答案正确填写在答题卡上，以下命题的逆命题为真命题的是，判断下列说法错误的是， 定义等内容，欢迎下载使用。
桐柏县2022-2023学年秋期第四次质量检测八年级数 学 试 题注意事项：1．答题前填写好自己的姓名．班级．考号等信息2．请将答案正确填写在答题卡上一、选择题（30分每题3分）1．下列运算中，正确的是（            ）A．  B．  C．   D．2．下列计算正确的是（　　）A．  B．  C．  D．3．以下命题的逆命题为真命题的是（       ）A．对顶角相等      B．如果a=0，b=0，那么ab=0C．若a>b，则    D．同旁内角互补，两直线平行4．【题文】如图，点B，F，C，E共线，∠B=∠E，BF=EC，添加一个条件，不能判断△ABC≌△DEF的是（       ）
 A．AB=DE    B．∠A=∠D   C．AC=DF   D．5．判断下列说法错误的是（          ）A．2是8的立方根     B．±4是64的立方根C．是的立方根    D．的立方根是6．如图所示，，，要使，需添加条件是（       ）
 A．   B．   C．   D．7．如图1，在边长为a的正方形中挖掉一个边长为b的小正方形（a>b），把余下的部分剪拼成一个如图2所示的长方形，通过计算两个图形阴影部分的面积，验证了一个等式，这个等式是（       ）
 A．    B．C．     D．8．如图是由两个直角三角形和三个正方形组成的图形，其中阴影部分的面积是（       ）
 A．16    B．25    C．144    D．1699． 定义：三角形三边的垂直平分线相交于一点，这个点叫做三角形的外心．如图，直线 ，，分别是边AB，AC的垂直平分线，直线和相交于点O，点O是△ABC的外心，交BC于点M，交BC于点N，分别连结AM，AN，OA，OB，OC．若OA=6cm，△OBC的周长为22cm，则△AMN的周长等于（　　）cm
 A．8    B．10    C．12    D．1410． 如图，我国古代的“赵爽弦图”是由四个全等的直角三角形和一个小正方形密铺构成的大正方形，若小正方形的面积为1，大正方形的面积为13，则直角三角形较短的直角边a与较长的直角边b的比的值是（　　）
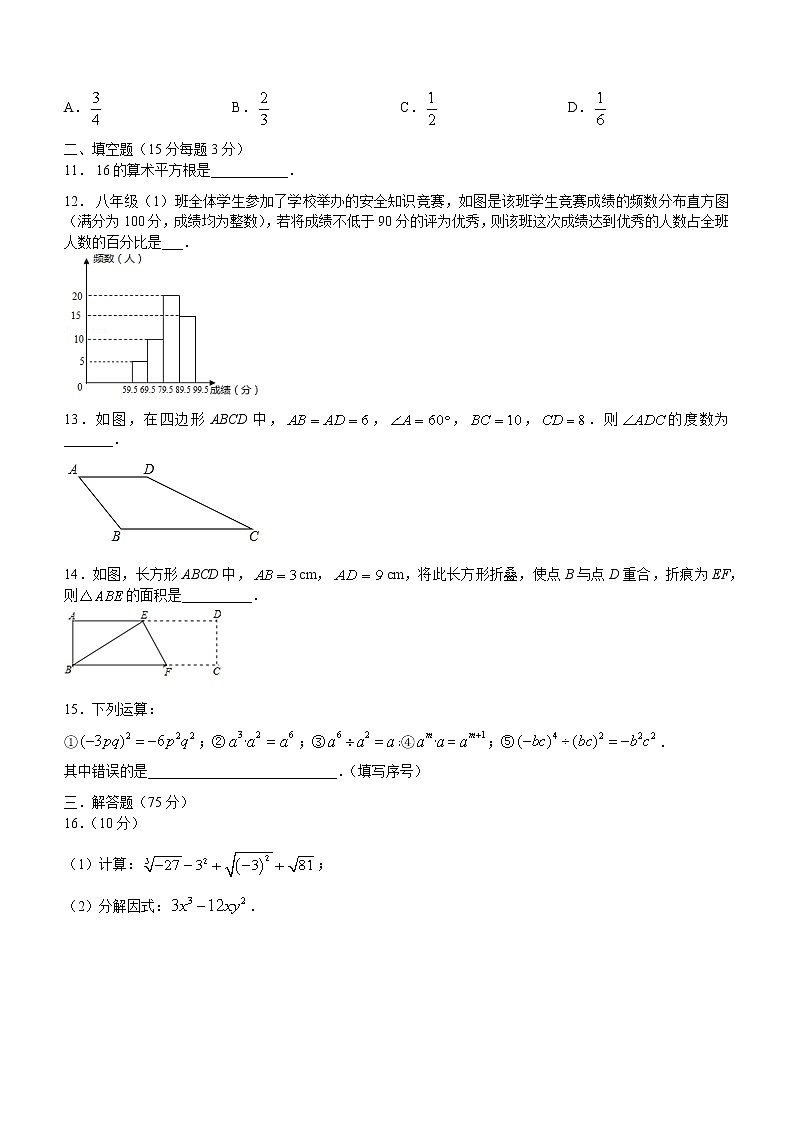
 A．     B．     C．     D．二、填空题（15分每题3分）11． 16的算术平方根是___________．12． 八年级（1）班全体学生参加了学校举办的安全知识竞赛，如图是该班学生竞赛成绩的频数分布直方图（满分为100分，成绩均为整数），若将成绩不低于90分的评为优秀，则该班这次成绩达到优秀的人数占全班人数的百分比是___．
 13．如图，在四边形ABCD中，，，，．则的度数为_______．
 14．如图，长方形ABCD中，cm，cm，将此长方形折叠，使点B与点D重合，折痕为EF，则的面积是__________．
 15．下列运算：
①；②；③﹔④；⑤．
其中错误的是___________________________．（填写序号）三．解答题（75分）16．（10分）（1）计算：；
（2）分解因式：．17．（9分） 如图，在△ABC中，∠B＝40°，∠C＝50°．

（1）按要求尺规作图：（不写作法，保留作图痕迹）
①作线段AB的垂直平分线，交AB于点F，交BC于点D：
②作∠CAD的平分线，交CD于点E．
（2）求∠DAE的度数．18．（9分）  先化简，再求值：
，其中．19．（9分） 如图，已知△ABC中，点D为BC边上一点，∠B=∠4，∠1=∠2=∠3，求证：BC=DE.
 20．（9分） 先化简，再求值：
（1），其中a=2，b=1；
（2），其中x=2，y=1．21．（9分） 证明命题“角平分线上的点到角的两边的距离相等”，要根据题意，画出图形，并用符号表示已知和求证，写出证明过程．下面是小明同学根据题意画出的图形，并写出了不完整的已知和求证．
已知：如图，∠AOC=∠BOC，

_______________________________________________________．
求证：___________________________________．
请你补全已知和求证，并写出证明过程．22．（9分）下面是某同学对多项式进行因式分解的过程．
解：设，
原式＝（y﹣1）（y＋3）＋4（第一步）
＝（第二步）
＝（第三步）
＝（第四步）
＝（第五步）
回答下列问题：
（1）该同学第三步到第四步运用了        ．　     　
A．提公因式法                                     B．平方差公式
C．两数和的完全平方公式                  D．两数差的完全平方公式
（2）该同学因式分解的结果是否彻底？        （填“彻底”或“不彻底”）．若不彻底，请直接写出因式分解的最后结果为        ．
（3）请你模仿以上方法尝试对多项式进行因式分解．23．（11分） 【教材呈现】如图是华师版八年级上册数学教材第69页的部分内容：


（1）【方法应用】如图①，在△ABC中，AB＝6，AC＝4，则BC边上的中线AD长度的取值范围是　       　．
（2）【猜想证明】如图②，在四边形ABCD中，，点E是BC的中点，若AE是∠BAD的平分线，试猜想线段AB．AD．DC之间的数量关系，并证明你的猜想；
（3）【拓展延伸】如图③，已知，点E是BC的中点，点D在线段AE上，∠EDF＝∠BAE，若AB＝5，CF＝2，直接写出线段DF的长． 参考答案1-5 CCDCB   6-10  DDBBB11．4  12． 30%  13．150°   14．   15．①②③⑤16． （1）原式；
（2）原式．
17．（1）解：①如图，FD即为所求；
②如图，AE即为所求；

（2）在△ABC中， ∵∠B=40°，∠C=50°，
∴∠BAC=180°-∠B-∠C=90°，∵DF是AB的垂直平分线，
∴，∴∠DAB=∠B=40°，
∴∠DAC=∠BAC-∠DAB=50°，∵AE平分∠DAC，
∴，
答：∠DAE的度数为25°．
18．解：

当时，原式
19．证：如图
 ∵，∴，∵∴，∴∴，，∴在和中∴（AAS），∴
20． （1）
解：原式
把a=2，b=1代入得：原式=；
（2）解：原式
把x=2，y=1代入得：原式=2×（2-1）=2
21． 解：已知：如图，∠AOC=∠BOC，点P在OC上，PD⊥OA于D，PE⊥OB于E，
求证：PD=PE，
证明：在△OPD和△OPE中，，
∴△OPD≌△OPE（AAS）  ∴PD=PE．
22． （1）解：运用了两数和的完全平方公式，故选：C；
（2）原式故答案为：不彻底，；
（3）设，
原式
，
即．
23．解：（1）延长AD到E，使AD＝DE，连接BE，

∵AD是BC边上的中线，∴BD＝CD，
在△ADC和△EDB中，，
∴△ADC≌△EDB（SAS），∴AC＝BE＝4，
在△ABE中，AB﹣BE＜AE＜AB+BE，
∴6﹣4＜2AD＜6+4，∴1＜AD＜5，
故答案为：1＜AD＜5．
（2）结论：AD＝AB+DC．
理由：如图②中，延长AE，DC交于点F，

∵，∴∠BAF＝∠F，
在△ABE和△FCE中，，
∴△ABE≌△FCE（AAS），∴CF＝AB，
∵AE是∠BAD的平分线，∴∠BAF＝∠FAD，
∴∠FAD＝∠F，∴AD＝DF，∵DC+CF＝DF，∴DC+AB＝AD．
（3）如图③，延长AE交CF的延长线于点G，

∵E是BC的中点，∴CE＝BE，∵，
∴∠BAE＝∠G，在△AEB和△GEC中，
，∴△AEB≌△GEC（AAS），
∴AB＝GC，∵∠EDF＝∠BAE，∴∠FDG＝∠G，
∴FD＝FG，∴AB＝DF+CF，∵AB＝5，CF＝2，
∴DF＝AB﹣CF＝3