初中数学冀教版九年级下册29.5 正多边形与圆示范课课件ppt

这是一份初中数学冀教版九年级下册29.5 正多边形与圆示范课课件ppt，共23页。PPT课件主要包含了图片欣赏，新课讲解，∴∠A∠B，多边形是正多边形，中心角，边心距，例题选讲，知一求二，抢答题，外接圆等内容，欢迎下载使用。

PPT模板： PPT素材：背景： PPT图表： PPT下载： PPT教程： 资料下载： 范文下载： 试卷下载： 教案下载： PPT论坛： PPT课件： 语文课件： 数学课件： 英语课件： 美术课件： 科学课件： 物理课件： 化学课件： 生物课件： 地理课件： 历史课件：
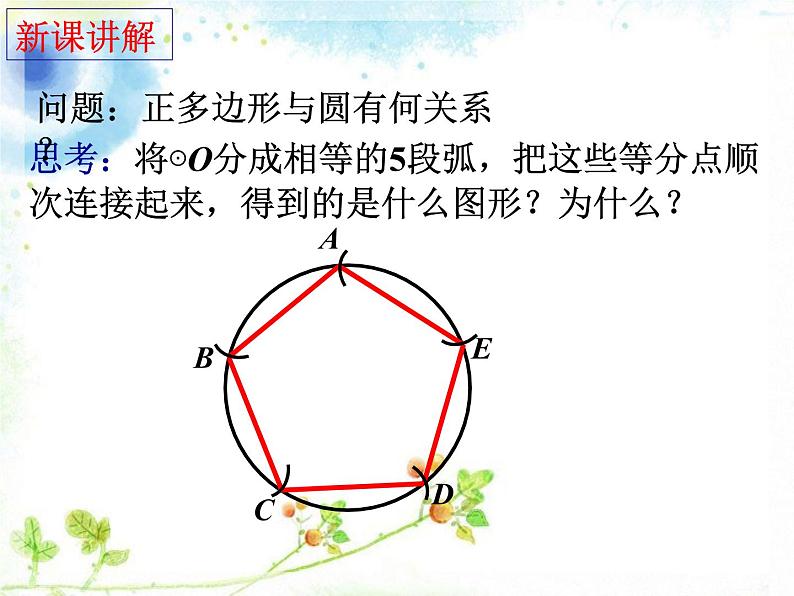
思考：将⊙O分成相等的5段弧，把这些等分点顺次连接起来，得到的是什么图形？为什么？
问题：正多边形与圆有何关系？
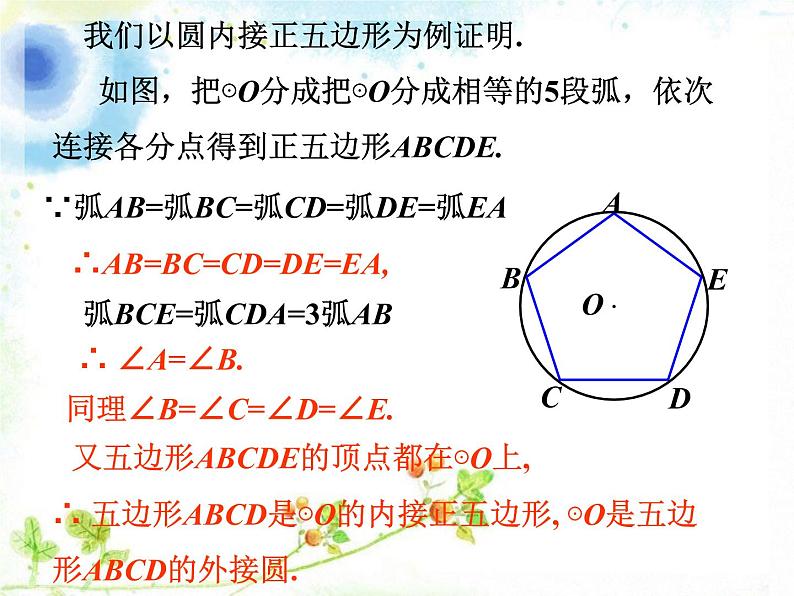
如图，把⊙O分成把⊙O分成相等的5段弧，依次连接各分点得到正五边形ABCDE.
∴AB=BC=CD=DE=EA,
同理∠B=∠C=∠D=∠E.
又五边形ABCDE的顶点都在⊙O上,
∴ 五边形ABCD是⊙O的内接正五边形, ⊙O是五边形ABCD的外接圆.
我们以圆内接正五边形为例证明.
∵弧AB=弧BC=弧CD=弧DE=弧EA
弧BCE=弧CDA=3弧AB
你知道正多边形与圆的关系吗？
正多边形和圆的关系非常密切,只要把一个圆分成相等的一些弧,就可以作出这个圆的内接正多边形,这个圆就是这个正多边形的外接圆.
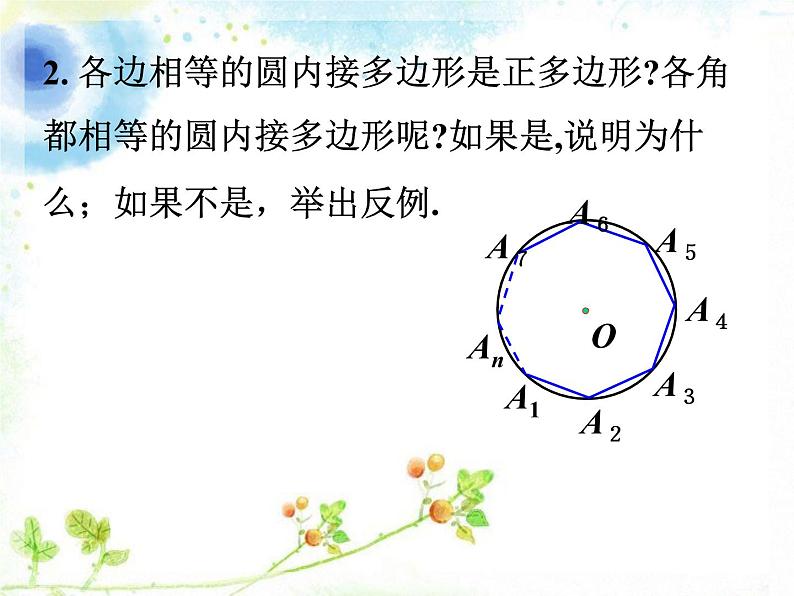
2. 各边相等的圆内接多边形是正多边形?各角都相等的圆内接多边形呢?如果是,说明为什么；如果不是，举出反例.
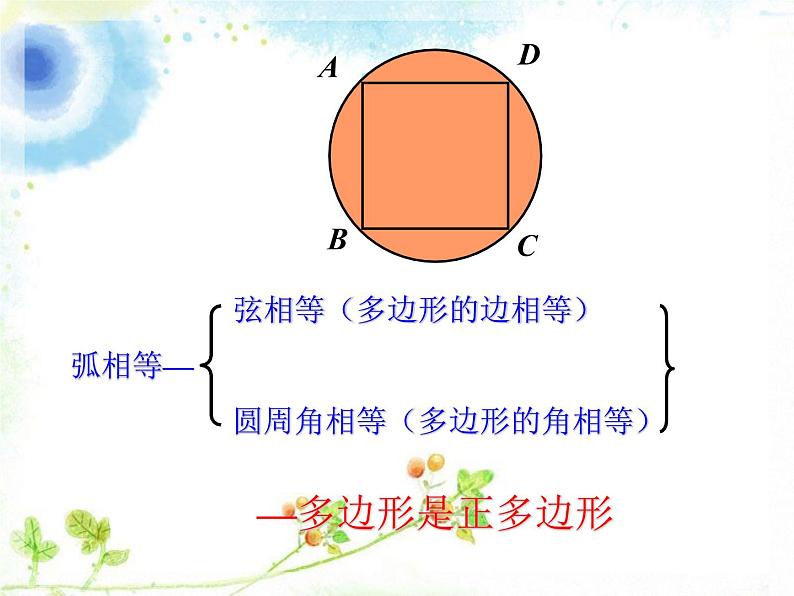
弦相等（多边形的边相等）弧相等— 圆周角相等（多边形的角相等）
正多边形每一边所对的圆心角叫做正多边形的中心角.
我们把一个正多边形的外接圆的圆心叫做这个正多边形的中心.
外接圆的半径叫做正多边形的半径.
中心到正多边形的一边的距离叫做正多边形的边心距.
正多边形中的有关概念：
既是外接圆的圆心，也是内切圆的圆心
正n边形的一个内角的度数是____________;中心角是___________;正多边形的中心角与外角的大小关系是________.
例1 用尺规作圆的内接正方形．已知：如图29-5-2，⊙O.求作：正方形ABCD内接于⊙O.
作法：（1）如图29-5-3，作两条互相垂直的直径AC，BD.
（2）顺次连接AB，BC，CD，DA.
由作图过程可知，四个中心角都是90°，所以AB=BC=CD=DA．
因为AC，BD都是直径，所以∠ABC=∠BCD=∠CDA＝∠DAB=90°.
即四边形ABCD为⊙O的内接正方形．
例2 如图29-5-4，△ABC为⊙O的内接正三角形．如果的⊙O半径为r，求这个正三角形的边长和边心距．
解：如图29-5-5，连接OB，过点O作OD⊥BC，垂足为D.在Rt△OBD中，∵∠OBD=30°，OB=r，∴OD= ，BD= ，BC=2BD= .即这个正三角形的边长为 ,边心距为 .
1.若正三角形的半径为4，则它的边心距是 ____，边长是_____.
2.有一个亭子，它的地基是半径为4m的正六边形（如图）求地基的周长和面积.
若正多边形的周长为l，边心距为r，则：S=_________.
重点：正三角形、正方形、 正六边形
1.O是正与　　 的圆心.
△ABC的中心，它是△ABC的
2、OB叫正△ABC的　它是正△ABC的 的半径. 　　　　　
3、OD叫作正△ABC的　　　　　它是正△ABC的 的半径.
怎样画一个正多边形呢？ 已知⊙O的半径为2cm，求作圆的内接正三角形.
①用量角器度量，使∠AOB=∠BOC=∠COA=120°． ②用量角器或30°角的三角板度量，使∠BAO=∠CAO=30°．
你能用以上方法画出正四边形、正五边形、正六边形吗？
你能尺规作出正六边形、正三角形、正十二边形吗？
以半径长在圆周上截取六段相等的弧，依次连结各等分点，则作出正六边形. 先作出正六边形，则可作正三角形，正十二边形，正二十四边形………
练习：用量角器作五角星
按照一定比例,画一个停车让行的交通标志的外缘
1.用量角器等分圆2.尺规作图等分圆
小结：画正多边形的方法