2023届广西省梧州市高三第一次模拟测试数学（文）试题（word版）

这是一份2023届广西省梧州市高三第一次模拟测试数学（文）试题（word版），共17页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
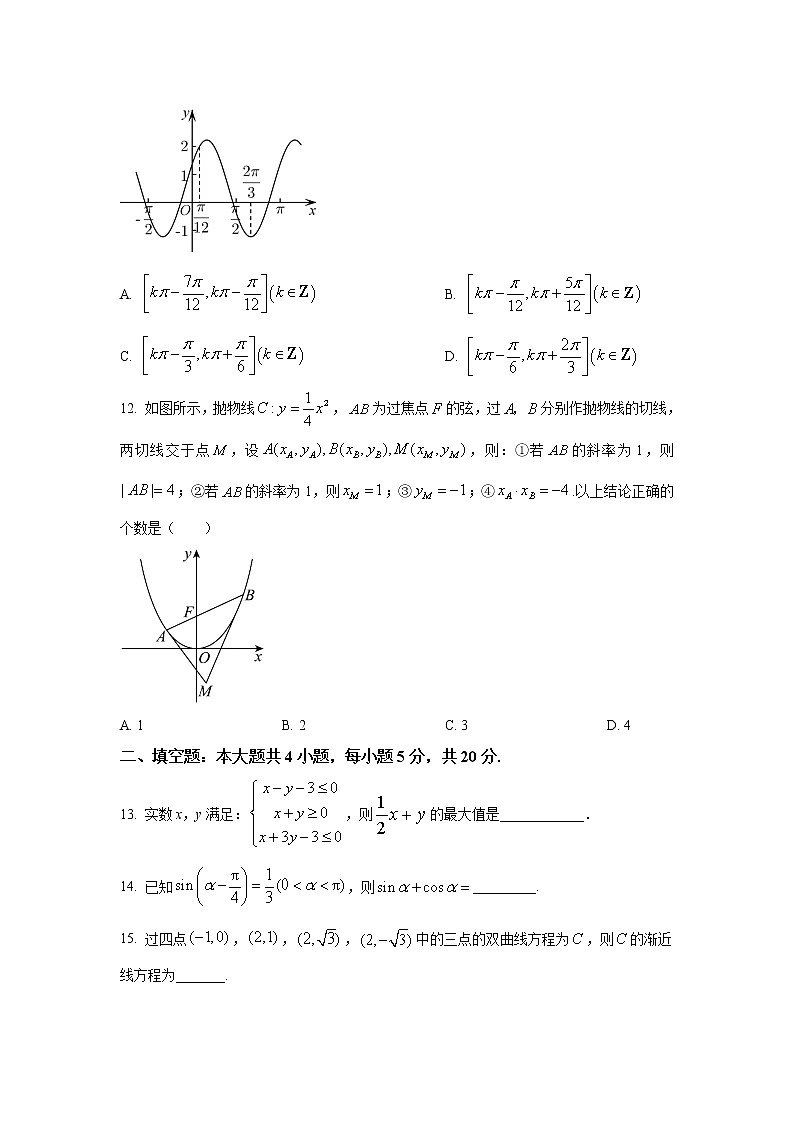
梧州市2023届高三第一次模拟测试文科数学一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，只有一项是符合题目要求的.1. 设集合，，，则（    ）A.  B.  C.  D. 2. 若复数z满足，则在复平面内的共轭复数对应的点位于（    ）A 第一象限 B. 第二象限 C. 第三象限 D. 第四象限3. 从某中学甲、乙两班各随机抽取10名同学，测量他们的身高（单位：），所得数据用茎叶图表示如图，由此可估计甲、乙两班同学的身高情况，则下列结论正确的是（    ）A. 甲乙两班同学身高的极差相等 B. 甲乙两班同学身高的平均值相等C. 甲乙两班同学身高的中位数相等 D. 乙班同学身高在以上的人数较多4. 已知向量，满足，，，则（    ）A 3 B.  C.  D. 45. 我们可以把看作每天“进步”率都是1%，一年后是；而把看作每天的“落后”率都是1%，一年后是.可以计算得到，一年后的“进步”是“落后”的倍.如果每天的“进步”率和“落后”率都是10%，至少经过（    ）天后，“进步”是“落后”的1000倍.（，）A. 31 B. 33 C. 35 D. 376. 在中，三个内角A，B，C所对的边分别为a，b，c，且.若，，则（    ）A. 2 B.  C. 4 D. 7. 直线与圆交两点.若，则的面积为（    ）A.  B.  C.  D. 8. 在正方体中，E，F分别是线段，的中点，则异面直线，EF所成角余弦值是（    ）A.  B.  C.  D. 9. 已知定义在R上的函数在上单调递增，若函数为偶函数，且，则不等式的解集为（    ）A.  B.  C.  D. 10. 在三棱锥中，已知平面，，.若三棱锥的各顶点都在球O的球面上，则球O的表面积为（    ）A.  B.  C.  D. 11. 若函数的部分图像如图所示，直线为函数图像的一条对称轴，则函数的单调递减区间为（    ）A.  B. C.  D. 12. 如图所示，抛物线，为过焦点的弦，过分别作抛物线的切线，两切线交于点，设，则：①若的斜率为1，则；②若的斜率为1，则；③；④.以上结论正确的个数是（    ）A. 1 B. 2 C. 3 D. 4二、填空题：本大题共4小题，每小题5分，共20分.13. 实数x，y满足：，则的最大值是____________．14. 已知，则_________.15. 过四点，，，中的三点的双曲线方程为，则的渐近线方程为_______.16. 已知函数，若关于x的方程有5个不同的实数根，则a的取值范围为_______.三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17. 已知为数列的前n项和，.（1）求数列的通项公式；（2）记，求前项的和.18. 近年来，随着社会对教育的重视，家庭的平均教育支出增长较快，某机构随机调查了某市2016-2022年的家庭教育支出（单位：万元），得到如下折线图.（附：年份代码1-7分别对应2016-2022年）.经计算得，，，，.（1）用线性回归模型拟合与关系，求出相关系数r，并说明与相关性的强弱；（参考：若，则线性相关程度一般，若，则线性相关程度较高，计算r时精确度为0.01）（2）求出与的回归直线方程；（3）若2024年该市某家庭总支出为10万元，预测2024年该家庭的教育支出.附：①相关系数；②在回归直线方程，，.19. 边长为1的正方形中，点M，N分别是DC，BC的中点，现将，分别沿AN，AM折起，使得B，D两点重合于点P，连接PC，得到四棱锥.（1）证明：平面平面；（2）求四棱锥的体积.20. 已知椭圆的长轴长为4，且经过点，．（1）求椭圆的方程；（2）直线的斜率为，且与椭圆交于，两点（异于点，过点作的角平分线交椭圆于另一点．证明：直线与坐标轴平行．21. 已知函数.（1）求函数的最小值；（2）证明：.（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22. 在直角坐标系中，直线的参数方程为（为参数），以为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．（1）求的极坐标方程和的直角坐标方程；（2）若与交于，两点，求的值．[选修4-5：不等式选讲]23. 已知函数．（1）求不等式的解集；（2）设函数最小值为m，且正实数a，b，c满足，求证：．                            梧州市2023届高三第一次模拟测试文科数学1.【答案】A2.【答案】D3.【答案】D4.【答案】D5.【答案】C6.【答案】B7.【答案】A8.【答案】C9.【答案】C10.【答案】D11.【答案】B12.【答案】B二、填空题：本大题共4小题，每小题5分，共20分.13. 【答案】##14. 【答案】15. 【答案】16. 【答案】三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答.（一）必考题：共60分.17. 已知为数列的前n项和，.（1）求数列的通项公式；（2）记，求前项的和.【答案】（1）    （2）【解析】【分析】（1）由题知数列是等比数列，公比为，首项为，进而得；（2）结合（1）得，进而分组求和即可.小问1详解】解：因为，所以，当时，，解得，当时，，，所以，即，所以，数列是等比数列，公比为，首项为，所以，数列的通项公式为.【小问2详解】解：由（1）知，所以，记前项的和为，所以，.18. 近年来，随着社会对教育的重视，家庭的平均教育支出增长较快，某机构随机调查了某市2016-2022年的家庭教育支出（单位：万元），得到如下折线图.（附：年份代码1-7分别对应2016-2022年）.经计算得，，，，.（1）用线性回归模型拟合与的关系，求出相关系数r，并说明与相关性的强弱；（参考：若，则线性相关程度一般，若，则线性相关程度较高，计算r时精确度为0.01）（2）求出与的回归直线方程；（3）若2024年该市某家庭总支出为10万元，预测2024年该家庭的教育支出.附：①相关系数；②在回归直线方程，，.【答案】（1），线性相关程度较高    （2）    （3）万元.【解析】【分析】（1）由公式计算相关系数并判断相关性即可；（2）由公式算，再由算即可；（3）2024年对应的年份代码，代入回归方程即可得到教育支出占比，即可预测2023年该家庭的教育支出【小问1详解】解：由题意得，，则，故，故，∵，∴与高度相关，即与的相关性很强．【小问2详解】解：根据题意，得，，∴关于的回归直线方程为．【小问3详解】解：由题知，2024年对应的年份代码，所以，当时，，所以，预测2024年该家庭的教育支出为（万元）．19. 边长为1的正方形中，点M，N分别是DC，BC的中点，现将，分别沿AN，AM折起，使得B，D两点重合于点P，连接PC，得到四棱锥.（1）证明：平面平面；（2）求四棱锥的体积.【答案】（1）证明见解析    （2）【解析】【分析】(1)先证明平面，即可证明出平面平面(2)先利用求出点到平面的距离，然后再根据四棱锥的体积公式进行计算，即可得出结果.【小问1详解】证明：在正方形中有，，，，又因为，所以平面，而平面，所以平面平面.【小问2详解】连接MN由题意可得，，，由，所以为直角三角形，即，，设点到平面的距离为，由得，，即，得，即四棱锥的体积为20. 已知椭圆的长轴长为4，且经过点，．（1）求椭圆的方程；（2）直线的斜率为，且与椭圆交于，两点（异于点，过点作的角平分线交椭圆于另一点．证明：直线与坐标轴平行．【答案】（1）；（2）证明见解析.【解析】分析】（1）由条件得：解得，，即可得到椭圆方程．（2）证明：欲证与坐标轴平行，即证直线的方程为；或，又因为平分，故只需证明，的斜率都存在时满足即可．当，的斜率不存在时，说明不满足题意．然后证明．设直线，，，，，联立，利用韦达定理结合的表达式，推出结果即可．【详解】（1）解：由条件得：解得，，椭圆．（2）证明：欲证与坐标轴平行，即证直线的方程为；或，又因为平分，故只需证明，的斜率都存在时满足即可．当，的斜率不存在时，即点或的坐标为，而经检验此时直线与椭圆相切，不满足题意．故，的斜率都存在，下证．设直线，，，，，联立，可得此时，，，．（※），（※）式的分子，直线与坐标轴平行．得证．【点睛】本题主要考查了求椭圆方程以及韦达定理的应用，属于中档题.21. 已知函数.（1）求函数的最小值；（2）证明：【答案】（1）0    （2）详见解析【解析】【分析】（1）首先求函数的导数，利用导数判断函数的单调性，即可求函数的最小值；（2）由（1）可知，令，不等式变形为，不等式右边裂项为，再用累加求和，即可证明不等式.【小问1详解】，，当时，，单调递减，当时，，单调递增，所以【小问2详解】由（1）知，即（当且仅当时等成立），令，则，所以，而，故，从而，，…，，累加可得，命题得证.【点睛】关键点点睛：本题第二问考查导数与数列的综合问题，问题的关键是从要证明的式子入手，将(1)的不等式变形为，再利用裂项相消法求和.（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按所做的第一题计分.[选修4-4：坐标系与参数方程]22. 在直角坐标系中，直线的参数方程为（为参数），以为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为．（1）求的极坐标方程和的直角坐标方程；（2）若与交于，两点，求的值．【答案】（1），    （2）【解析】【分析】（1）消去参数得到直线的普通方程，从得到其极坐标方程，根据将曲线的极坐标方程化为直角坐标方程；（2）把代入曲线的极坐标方程，即可求出，从而得解.【小问1详解】解：因为直线的参数方程为（为参数），所以消去直线参数方程中的参数得，即，显然直线过原点，倾斜角为，直线的极坐标方程为．曲线的极坐标方程化为，将代入得：，即，所以的极坐标方程为，的直角坐标方程为．【小问2详解】解：把代入得，解得，所以，所以．[选修4-5：不等式选讲]23. 已知函数．（1）求不等式的解集；（2）设函数的最小值为m，且正实数a，b，c满足，求证：．【答案】（1）    （2）证明见详解【解析】【分析】（1）分段讨论去绝对值即可求解；（2）利用绝对值不等式可求得，再利用基本不等式即可证明.【小问1详解】由题意可得：，当时，则，解得；当时，则，解得；当时，则，解得；综上所述：不等式的解集为.【小问2详解】∵，当且仅当时等号成立，∴函数的最小值为，则，又∵，当且仅当，即时等号成立；，当且仅当，即时等号成立；，当且仅当，即时等号成立；上式相加可得：，当且仅当时等号成立，∴.