2.3平行线的性质寒假预习自测北师大版数学七年级下册

这是一份2.3平行线的性质寒假预习自测北师大版数学七年级下册，共26页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
2.3平行线的性质寒假预习自测北师大版数学七年级下册
限时：60分钟；满分：100分
学校:___________姓名：___________班级：___________考号：___________

一、单选题(共30分)
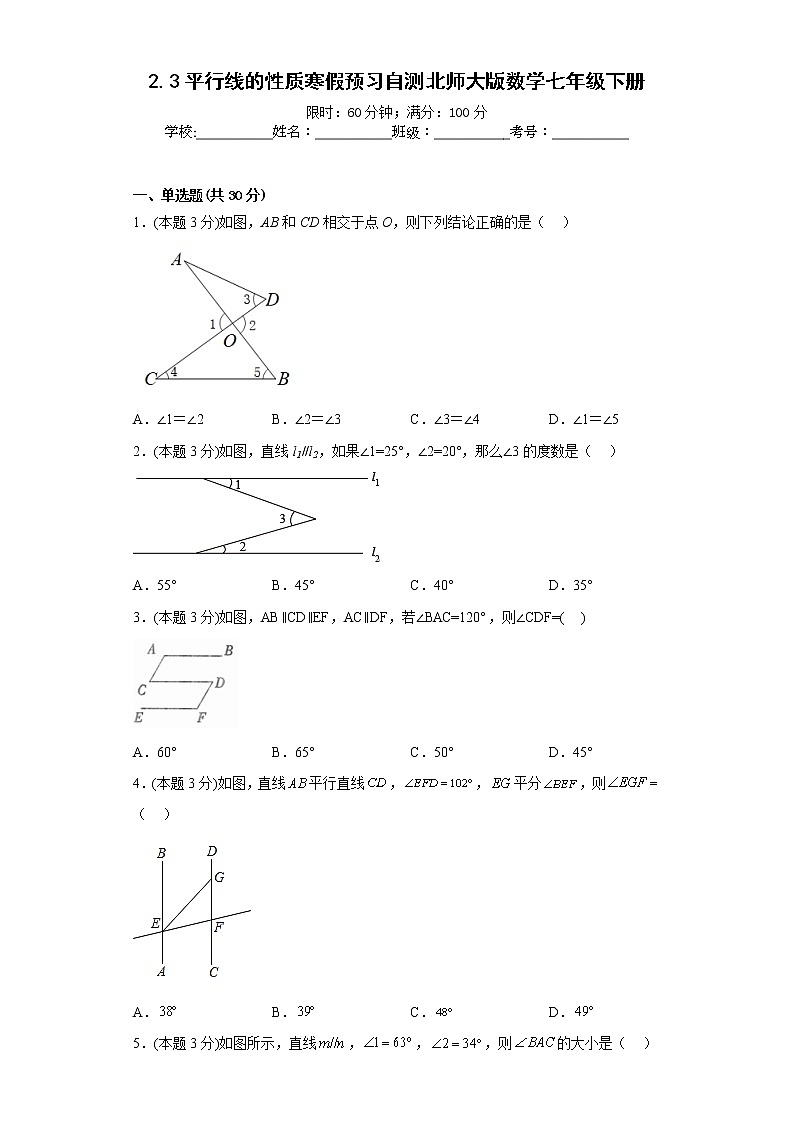
1．(本题3分)如图，AB和CD相交于点O，则下列结论正确的是（    ）

A．∠1＝∠2 B．∠2＝∠3 C．∠3＝∠4 D．∠1＝∠5
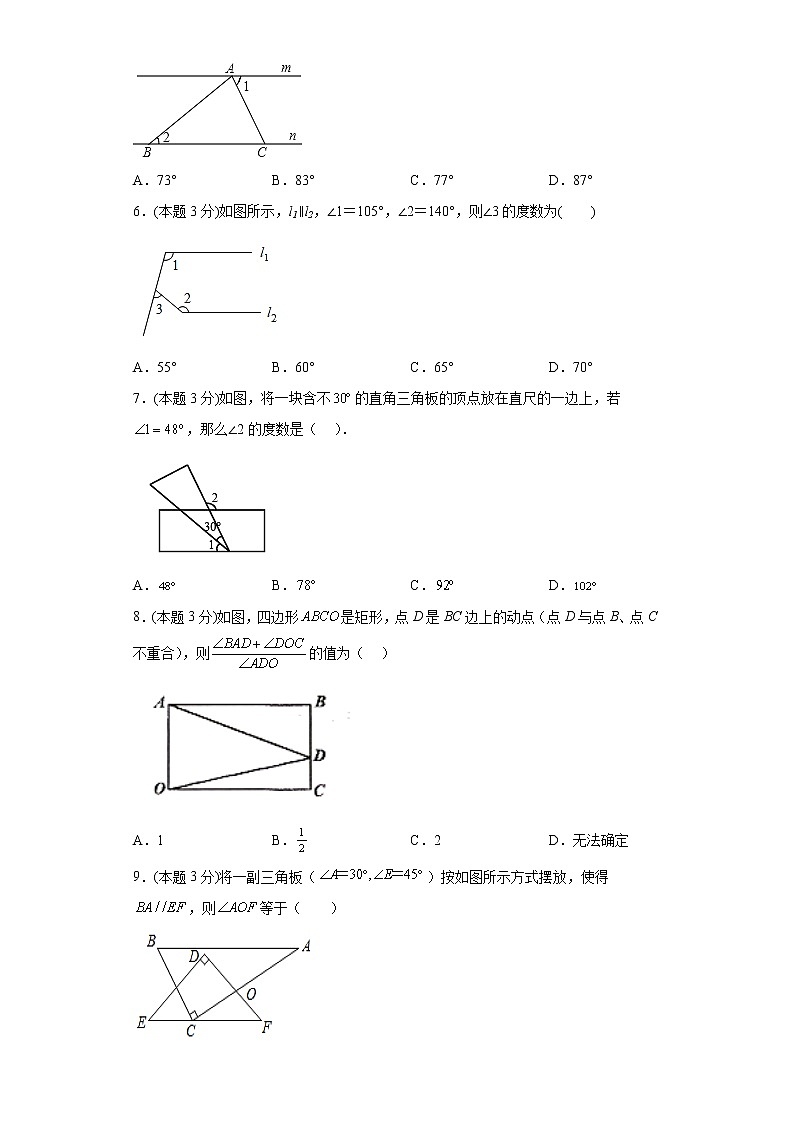
2．(本题3分)如图，直线l1//l2，如果∠1=25°，∠2=20°，那么∠3的度数是（    ）

A．55° B．45° C．40° D．35°
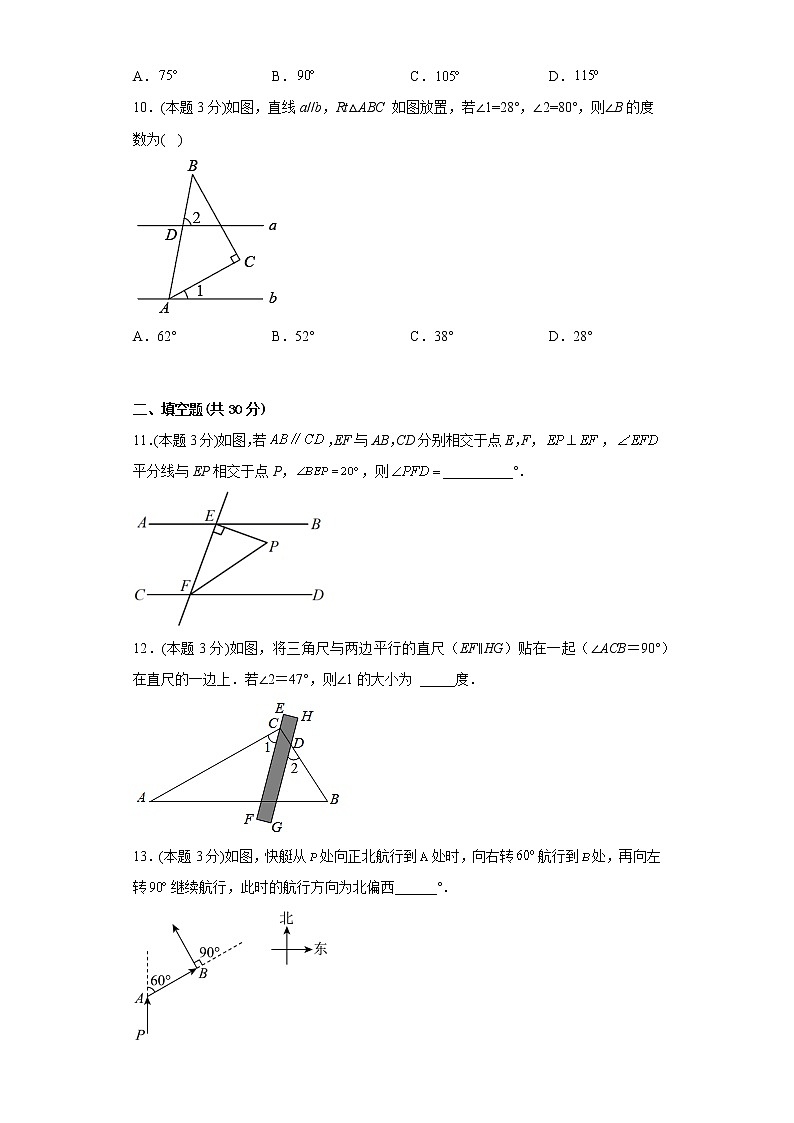
3．(本题3分)如图，AB∥CD∥EF，AC∥DF，若∠BAC=120°，则∠CDF=(    )

A．60° B．65° C．50° D．45°
4．(本题3分)如图，直线平行直线，，平分，则（    ）

A． B． C． D．
5．(本题3分)如图所示，直线，，，则的大小是（    ）

A．73° B．83° C．77° D．87°
6．(本题3分)如图所示，l1∥l2，∠1＝105°，∠2＝140°，则∠3的度数为(　　)

A．55° B．60° C．65° D．70°
7．(本题3分)如图，将一块含不的直角三角板的顶点放在直尺的一边上，若，那么∠2的度数是（    ）．

A． B． C． D．
8．(本题3分)如图，四边形是矩形，点D是BC边上的动点（点D与点B、点C不重合），则的值为（    ）

A．1 B． C．2 D．无法确定
9．(本题3分)将一副三角板（）按如图所示方式摆放，使得，则等于（　　）

A． B． C． D．
10．(本题3分)如图，直线a//b，Rt△ABC 如图放置，若∠1=28°，∠2=80°，则∠B的度数为(   )

A．62° B．52° C．38° D．28°

二、填空题(共30分)
11．(本题3分)如图，若，EF与AB，CD分别相交于点E，F，，平分线与EP相交于点P，，则__________°．

12．(本题3分)如图，将三角尺与两边平行的直尺（EF∥HG）贴在一起（∠ACB＝90°）在直尺的一边上．若∠2＝47°，则∠1的大小为 _____度．

13．(本题3分)如图，快艇从处向正北航行到处时，向右转航行到处，再向左转继续航行，此时的航行方向为北偏西______°．

14．(本题3分)一副三角板按如图所示叠放，其中，，，且，则______度．

15．(本题3分)已知：如图，，则∠4的度数是___________．

16．(本题3分)如图，直线，平分，若，则度数是_________．

17．(本题3分)光线在不同介质中传播速度不同，从一种介质射向另一种介质时会发生折射．如图，水面与水杯下沿平行，光线从水中射向空气时发生折射，光线变成，点在射线上，已知，，则的度数为______．

18．(本题3分)如图，已知，，，则______．

19．(本题3分)一副直角三角尺叠放如图1所示，现将45°的三角尺固定不动，将含30°的三角尺绕顶点顺时针转动至图2位置的过程中，使两块三角尺至少有一组边互相平行．如图3：当时，BC∥DE．则其余符合条件的度数为______．

20．(本题3分)如图，，∠DCE=118°，∠AEC的角平分线EF与GF相交于点F，∠BGF=132°，则∠F的度数是__．


三、解答题(共40分)
21．(本题8分)问题情境：
在综合实践课上，老师组织七年级（2）班的同学开展了探究两角之间数量关系的数学活动，如图，已知射线，连接，点P是射线上的一个动点（与点A不重合），，分别平分和，分别交射线于点C，D．

探索发现：
“快乐小组”经过探索后发现：
(1)当时，求证：．
(2)不断改变的度数，与却始终存在某种数量关系，
当则_______度，
当时，则_______度，（用含x的代数式表示）
操作探究：
(3)“智慧小组”利用量角器量出和的度数后，探究二者之间的数量关系．他们惊奇地发现，当点P在射线上运动时，无论点P在上的什么位置，与之间的数量关系都保持不变，请写出它们的关系，并说明理由．
22．(本题8分)将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起（其中，，；）．

（1）①若，则的度数为_____________；
②若，则的度数为_____________．
（2）由（1）猜想与的数量关系，并说明理由．
（3）当且点E在直线AC的上方时，这两块三角尺是否存在一组边互相平行？若存在，请写出角度所有可能的值（不必说明理由）；若不存在，请说明理由．
23．(本题8分)如图，已知直线．

(1)在图1中，点E在直线AB上，点F在直线CD上，点G在AB、CD之间，若，，则______；
(2)如图2，若FN平分，延长GE交FN于点M，EM平分，当时，求的度数；
(3)如图3，直线MF平分，直线NE平分相交于点H，试猜想与的数量关系，并说明理由．
24．(本题8分)如图,DB∥FG∥EC,∠ABD=60°,∠ACE=36°,AP平分∠BAC．求∠PAG的度数．

25．(本题8分)如图，已知三角形EFG的顶点E，F分别在直线AB和CD上，且，若，，．

(1)当时，求的度数．
(2)设，，求和的数量关系（用含，的等式表示）

参考答案：
1．A
【分析】根据平行线的性质和对顶角的性质进行判断．
【详解】解：A、∵∠1与∠2是对顶角，
∴∠1＝∠2，本选项说法正确；
B、∵AD与AB不平行，
∴∠2≠∠3，本选项说法错误；
C、∵AD与CB不一定平行，
∴∠3≠∠4，本选项说法错误；
D、∵CD与CB不平行，
∴∠1≠∠5，本选项说法错误；
故选：A．
【点睛】本题考查平行线的应用，熟练掌握平行线的性质和对顶角的意义与性质是解题关键．
2．B
【分析】过∠3的顶点作，根据平行线的性质与判定，可得．
【详解】解：如图，过∠3的顶点作

，
l1//l2，
，
，
∠1=25°，∠2=20°，
，
故选B．
【点睛】本题考查了根据平行线的性质与判定求角度，掌握平行线的性质与判定是解题的关键．
3．A
【分析】根据两直线平行，同旁内角互补由AB∥CD得到∠BAC+∠ACD=180°，可计算出∠ACD=60°，然后由AC∥DF，根据平行线的性质得到∠ACD=∠CDF=60°．
【详解】∵AB∥CD，
∴∠BAC+∠ACD=180°，
∵∠BAC=120°，
∴∠ACD=180°-120°=60°，
∵AC∥DF，
∴∠ACD=∠CDF，
∴∠CDF=60°．
故选A．
【点睛】本题考查了平行线的性质：两直线平行，内错角相等；两直线平行，同旁内角互补．
4．B
【分析】根据可知，进而求出，再根据平分可，再根据平行线的性质知．
【详解】解：，
（两直线平行，同旁内角互补），
．
平分，
．
，
（两直线平行，内错角相等）．
故选B．
【点睛】本题考查平行线的性质，和角平分线的定义．熟练掌握相关知识点是解题的关键．
5．B
【分析】根据平行线性质，证得∠2=∠3，根据∠1+∠3+∠BAC=180°，求解即可
【详解】解：如图，∵直线，
∴∠2=∠3，
∵，，∠1+∠3+∠BAC=180°，
∴∠BAC=83°，

故选：B．
【点睛】本题考查了平行线的基本性质，平角的定义，灵活运用平行线的性质是解题的关键．
6．C
【分析】首先过点A作AB∥l1，由l1∥l2，即可得AB∥l1∥l2，然后根据两直线平行，同旁内角互补，即可求得∠4与∠5的度数，又由平角的定义，即可求得∠3的度数．
【详解】解：

过点A作AB∥l1，
∵l1∥l2，
∴AB∥l1∥l2，
∴∠1+∠4=180,∠2+∠5=180，
∵∠1=105,∠2=140 ，
∴∠4=75,∠5=40，
∵∠4+∠5+∠3=180，
∴∠3=65.
故选：C.
【点睛】本题考查的知识点是平行线的性质，解题的关键是熟练的掌握平行线的性质.
7．D
【分析】利用已知角的度数结合平行线的性质得出答案．
【详解】解：∵将一块含有30°的直角三角形的顶点放在直尺的边上，∠1=48°，
∴∠2=∠3=180°-48°-30°=102°
故选：D．
【点睛】此题主要考查平行线的性质，正确得出∠3的度数是解题的关键．
8．A
【分析】过点D作交AO于点E，由平行的性质可知，等量代换可得的值.
【详解】解：如图，过点D作交AO于点E，

四边形是矩形





故选：A.
【点睛】本题主要考查了平行线的性质，灵活的添加辅助线是解题的关键.
9．A
【分析】根据平行线的性质和三角形外角的性质进行计算，即可得到答案.
【详解】解：，
．
，
．
故选．

【点睛】本题考查平行线的性质和三角形外角的性质，解题的关键是掌握平行线的性质和三角形外角的性质.
10．C
【分析】如图：根据两直线平行、同位角相等可得∠1+∠3=∠2，进而求得∠3，再根据直角三角形的性质求得∠B即可．
【详解】解：如图，∵ab,
∴∠1+∠3=∠2，
∵∠3=∠2-∠1=80°-28°=52°，
∵∠ACB=90°，
∴∠B+∠3 =90°，
∴∠B=90°-52°=38°．
故答案为：C．

【点睛】本题主要考查了平行线的性质、直角三角形的性质等知识点，灵活应用平行线的性质成为解答本题的关键．
11．
【分析】由题可求出，然后根据两直线平行，同旁内角互补可知，根据角平分线的定义可得到结果．
【详解】∵，
∴，
∵，
∴，
∵，
∴，
∵平分，
∴．
【点睛】本题考查了平行线的性质与角平分线的定义，以及三角形的内角和定理，注意数形结合思想是解题关键．
12．43
【分析】先根据平行线的性质求出∠2的度数，再由∠1与∠3互余即可得出结论．
【详解】解：如图所示：
∵，，
∴
又∵，，
∴，
∴．
故答案为：．

【点睛】本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
13．
【分析】根据平行线的性质与方位角的定义即可求解．
【详解】解：如图，

∵，，
∴，
∴，
此时的航行方向为：北偏西；
故答案为：．
【点睛】此题主要考查方位角，解题的关键是熟知方位角的定义及平行线的性质．
14．45
【分析】首先根据AC∥DE得到∠ACD=∠D，再根据余角的知识求出∠BCD的度数．
【详解】∵AC∥DE，
∴∠ACD=∠D=45°，
∵∠ACB=90°，
∴∠BCD=∠ACB-∠ACD=45°，
故答案为：45．
【点睛】本题主要考查了平行线的性质和余角的性质，解答本题的关键是掌握两直线平行内错角相等．
15．126°．
【分析】由∠1=∠2及对顶角相等可得出∠1=∠5，利用“同位角相等，两直线平行”可得出l1∥l2，利用“两直线平行，同旁内角互补”可求出∠6的度数，再利用对顶角相等可得出∠4的度数．
【详解】解：给各角标上序号，如图所示．

∵∠1=∠2，∠2=∠5，
∴∠1=∠5，
∴l1∥l2，
∴∠3+∠6=180°．
∵∠3=54°，
∴∠6=180°-54°=126°，
∴∠4=∠6=126°．
故答案为：126°．
【点睛】本题考查了平行线的判定与性质，牢记平行线的各判定与性质定理是解题的关键．
16．##40度
【分析】根据邻补角的定义、角平分线的定义及平行线的性质求解即可．
【详解】解：，
，
平分，
，
，
，
故答案为：．
【点睛】此题考查了平行线的性质、角平分线的定义，熟记平行线的性质定理是解题的关键．
17．##25度
【分析】根据平行线的性质求得，根据即可求解．
【详解】解：∵，
∴．
∵，
∴；
故答案为25°．
【点睛】本题考查了平行线的性质与判定，掌握平行线的性质与判定是解题的关键．
18．##110度
【分析】由已知条件得到内错角相等，进而确定出与平行，根据两直线平行同位角相等及邻补角性质确定出所求即可．
【详解】
∵
∴
∴
∴
∵
∴
∴
故答案为：．
【点睛】本题考查了平行线的判定与性质，熟练掌握平行线的判定与性质是解题的关键．
19．60°或105°或135°

【分析】分四种情况进行讨论，分别依据平行线的性质进行计算即可得到∠CAE的度数．
【详解】解：如图2，当BC∥DE时，∠CAE=45°-30°=15°；

如图，当AE∥BC时，∠CAE=90°-30°=60°；

如图，当DE∥AB（或AD∥BC）时，∠CAE=45°+60°=105°；

如图，当DE∥AC时，∠CAE=45°+90°=135°．

综上所述，旋转后两块三角板至少有一组边平行，则∠CAE（0°＜∠CAE＜180°）其它所有可能符合条件的度数为60°或105°或135°．
故答案为：60°或105°或135°．
【点睛】本题考查的是平行线的判定与性质，根据题意画出图形，利用平行线的性质及直角三角板的性质求解是解答此题的关键．
20．11°##11度
【分析】根据平行线的性质，得出∠AEC=118°，根据角平分线的定义得出∠AEF=∠FEC=59°，根据∠BGF=132°，得出，根据三角形外角的性质，即可得出答案．
【详解】解：∵，，
∴∠AEC=118°，
∵∠AEC的角平分线EF与GF相交线于点F，
∴∠AEF=∠FEC=59°，
∵∠BGF=132°，
∴，
∴．
故答案为：11°．
【点睛】本题主要考查的是平行线的性质，角平分线的性质和三角形外角的性质，熟练掌握两直线平行，内错角相等，是解题的关键．
21．(1)见解析
(2)         
(3)，理由见解析

【分析】（1）根据平行线的性质可求得，再根据角平分线的定义求得即可证得结论；
（2）根据平行线的性质和角平分线的定义推出，进而求解即可；
（3）根据平行线的性质和角平分线的定义得到，，，进而解答即可．
【详解】（1）证明：∵，
∴，
又∵，
∴．
∵，分别平分和，
∴，，
∴，
∴．
（2）解：∵，分别平分和，
∴，，
∴，
∵，
∴，
∴，
∴．
当时，则，
当时，则；
故答案为：，；
（3）解：.理由如下：
∵平分，
∴，
∵，
∴，，
∴．
【点睛】本题考查角平分线的定义、平行线的性质，熟练掌握平行线的性质，能借助图形进行角度运算是解答的关键．
22．（1）①；②；（2），理由详见解析；（3）∠ACE=45°或30°或120°或135°或165°
【分析】（1）①先求出∠ACE，即可求出∠ACB；
②先求出∠ACE，即可求出∠DCE；
（2）根据题意可得，，从而求出与的数量关系；
（3）根据平行线的判定定理和边的平行关系分类讨论，然后画出对应的图形即可得出结论．
【详解】解：（1）①∵，∠ACD=∠BCE=90°
∴∠ACE=∠ACD－∠DCE=45°
∴∠ACB=∠ACE＋∠BCE=135°
故答案为：．
②∵，∠ACD=∠BCE=90°
∴∠ACE=∠ACB－∠BCE=50°
∴∠DCE=∠ACD－∠ACE =40°
故答案为：．
（2）．理由如下
∵，，
∴．
∵，，
∴
∴．
（3）①当时，

∵
∴
∴，
②当时，设CE与AD交于点F，如下图所示

∵∠A=60°，∠BCE=90°
∴∠AFC=180°－∠ACE－∠A=90°
∴∠AFC=∠BCE
∴．
③当时，如下图所示

∵∠ACD=90°，∠D=30°
∴∠DCE=∠ACE－∠ACD=30°
∴∠DCE=∠D
∴．
④当时，如下图所示

∵∠ACD=90°，∠E=45°
∴∠DCE=∠ACE－∠ACD=45°
∴∠DCE=∠E
∴．
⑤当时，过点C作CG∥AD，如下图所示

∴∠D=∠DCG=30°
∵∠ACD=90°，∠E=45°
∴∠GCE=∠ACE－∠ACD－∠DCG=45°
∴∠E=∠GCE
∴BE∥CG
∴．
综上所述：∠ACE=45°或30°或120°或135°或165°．
【点睛】此题考查的是角的和与差和平行线的判定，掌握各个角的关系和平行线的各个判定定理是解决此题的关键．
23．(1)45°
(2)
(3)∠EGF＝2∠EHF；理由见解析

【分析】（1）过G作，依据，即可得到∠1＝∠EGH，∠2＝∠FGH，进而得出∠2的度数；
（2）过G作，过N作，依据平行线的性质以及角的和差关系，即可得到∠AEN的度数；
（3）过H作，过G作，依据平行线的性质以及角的和差关系，即可得到∠G与∠H的数量关系．
【详解】（1）解：过G作，如图所示：

∵，
∴，
∴∠1＝∠EGH，∠2＝∠FGH，
∴∠1＋∠2＝∠EGF，即30°＋∠2＝75°，
∴∠2＝45°．
故答案为：45°．
（2）∵FN平分∠CFG，EM平分∠AEN，
∴可设∠AEM＝∠NEM＝α，∠CFN＝∠GFN＝β，
过G作，过N作，

∵，
∴，
∴∠QNF＝∠CFN＝β，∠QNE＝∠AEN＝2α，∠PGE＝∠AEM＝α，∠PGF＝∠DFG＝180°−2β，
∴∠FNE＝∠QNF-∠QNE＝β−2α，∠FGE＝∠PGE＋∠PGF＝α＋180°−2β，
又∵∠FNE＋∠FGE＝54°，
∴β−2α＋（α＋180°−2β）＝54°，
∴α＝24°，
∴∠AEN＝2α＝48°．
（3）猜想：∠G＝2∠H．理由：
∵MF平分∠CFG，NE平分∠AEG，
∴可设∠AEN＝∠NEG＝α，∠CFM＝∠GFM＝β，
过H作，过G作，如图所示：

∵，
∴，
∴∠QGE＝∠AEG＝2α，∠QGF＝∠CFG＝2β，∠PHM＝∠CFM＝β，∠PHN＝∠AEN＝α，
∴∠EGF＝∠QGE−∠QGF＝2α−2β，∠EHF＝∠PHN−∠PHM＝α−β，
∴∠EGF＝2∠EHF．
【点睛】本题主要考查了平行线的性质，解决问题的关键是作平行线构造内错角或同位角，利用平行线的性质以及角的和差关系进行推算．
24．12°
【详解】试题分析：本题主要利用两直线平行，同旁内角互补以及角平分线的定义进行解答．
试题解析：解：∵DB∥FG∥EC，∴∠BAG=∠ABD=60°，∠GAC=∠ACE=36°，
∴∠BAC=∠BAG+∠GAC=96°．∵AP是∠BAC的平分线，∴∠PAC=∠BAC=48°，∴∠PAG=∠PAC﹣∠GAC=48°﹣36°=12°，即∠PAG=12°．
点睛：本题考查了平行线的性质．两直线平行时，应该想到它们的性质，由两直线平行的关系得到角之间的数量关系，从而达到解决问题的目的．
25．(1)
(2)

【分析】（1）先根据平行线的性质以及角的和差可得，再由平角的性质可得，进而得到可得，然后再将代入求解即可；
（2）由图形可知、，则，再结合（1）的即可解答．
（1）
解： ∵
∴
∵，
∴，即
又∵
∴，解得：．
（2）
解：∵，，
∴
又由（1）知
∴．
【点睛】本题主要考查了平行线的性质、直角三角尺、角的和差等知识点，掌握平行线的性质成为解答本题的关键．