4.3探索三角形全等的条件寒假预习自测北师大版数学七年级下册

这是一份4.3探索三角形全等的条件寒假预习自测北师大版数学七年级下册，共25页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
4.3探索三角形全等的条件寒假预习自测北师大版数学七年级下册
限时：60分钟；满分：100分
学校:___________姓名：___________班级：___________考号：___________

一、单选题(共30分)
1．(本题3分)一块三角形玻璃不慎被小明摔成了四片碎片（如图所示），小明经过仔细的考虑认为只要带其中的两块碎片去玻璃店，就可以让师傅配一块与原玻璃一样的玻璃．你认为下列四个答案中考虑最全面的是（　　）

A．带其中的任意两块去都可以 B．带1、4或2、3去就可以了
C．带1、4或3、4去就可以了 D．带1、2或2、4去就可以了
2．(本题3分)下列说法不正确的是（   ）
A．两条直角边对应相等的两个直角三角形全等 B．一锐角和斜边对应相等的两个直角三角形全等
C．斜边和一直角边对应相等的两个直角三角形全等 D．有两边相等的两个直角三角形全等
3．(本题3分)如图，，，，点，，在同一直线上，若，，则的度数是（    ）

A． B． C． D．
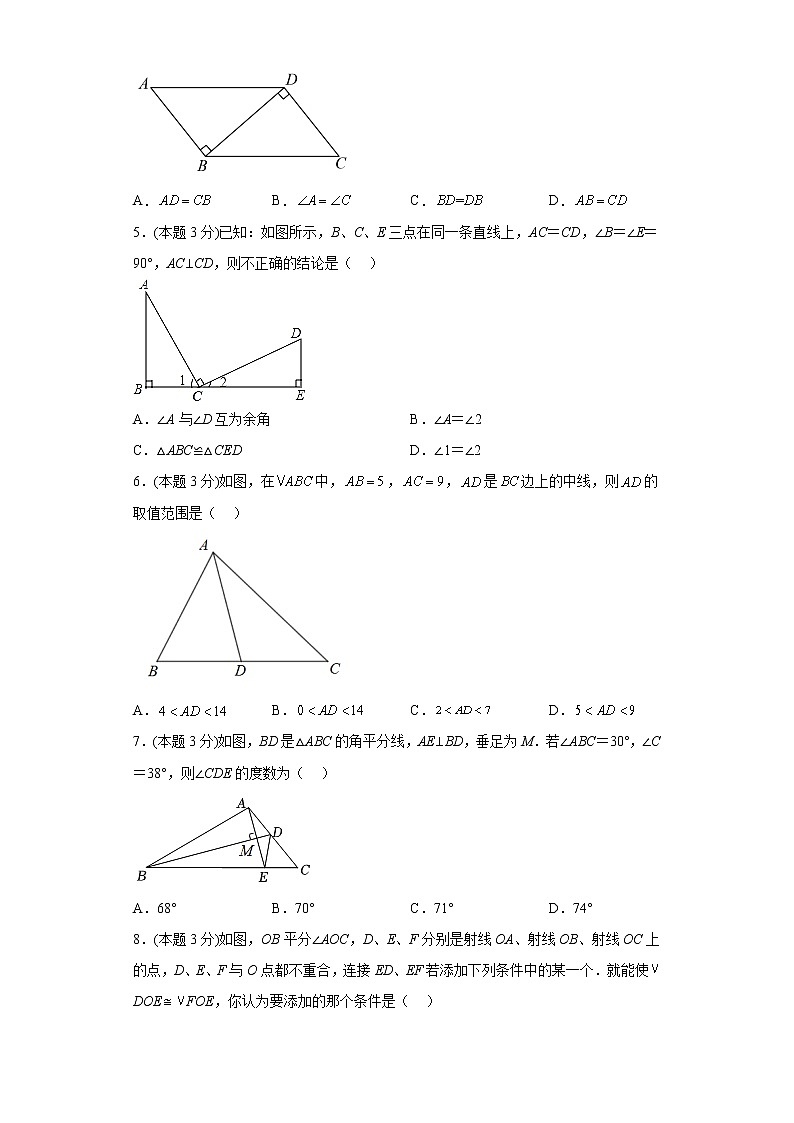
4．(本题3分)如图，已知，，若用“”判定和全等，则需要添加的条件是（    ）

A． B． C． D．
5．(本题3分)已知：如图所示，B、C、E三点在同一条直线上，AC＝CD，∠B＝∠E＝90°，AC⊥CD，则不正确的结论是（    ）

A．∠A与∠D互为余角 B．∠A＝∠2
C．△ABC≌△CED D．∠1＝∠2
6．(本题3分)如图，在中，，，是边上的中线，则的取值范围是（    ）

A． B． C． D．
7．(本题3分)如图，BD是△ABC的角平分线，AE⊥BD，垂足为M．若∠ABC＝30°，∠C＝38°，则∠CDE的度数为（    ）

A．68° B．70° C．71° D．74°
8．(本题3分)如图，OB平分∠AOC，D、E、F分别是射线OA、射线OB、射线OC上的点，D、E、F与O点都不重合，连接ED、EF若添加下列条件中的某一个．就能使DOEFOE，你认为要添加的那个条件是（    ）

A．OD=OE B．OE=OF C．∠ODE =∠OED D．∠ODE=∠OFE
9．(本题3分)如图，，，．下列结论中：（1）；（2）；（3）；（4）．正确的个数是（  　  ）．

A．1 B．2 C．3 D．4
10．(本题3分)如图，已知点A、D、C、F在同一条直线上，∠B=∠E =90°，AB=DE，若添加一个条件后，能用“HL”的方法判定Rt△ABC≌Rt△DEF，添加的条件可以是（　　）

A．BC=EF B．∠BCA=∠F C．AB∥DE D．AD=CF

二、填空题(共30分)
11．(本题3分)如图，在中，，于点E，于点D，请你添加一个条件__________，使（填一个即可）．

12．(本题3分)如图，在△ABC中，∠ACB＝90°，AC＝BC，BE⊥CE，AD⊥CE于D，AD＝2，BE＝1．则DE＝________．

13．(本题3分)如图，BD是△ABC的中线，E为AB边上一点，且，连接CE交BD于F，连接AF并延长交BC于点G，则______．

14．(本题3分)如图，∠C＝90°，AC＝20，BC＝10，AX⊥AC，点P和点Q同时从点A出发，分别在线段AC和射线AX上运动，且AB＝PQ，当AP＝_____时，以点A，P，Q为顶点的三角形与△ABC全等．

15．(本题3分)如图是由九个边长为1的小正方形拼成的大正方形，图中∠1＋∠2＋∠3＋∠4＋∠5的度数为______．

16．(本题3分)如图，，cm，cm，点P在线段AC上，以每秒2cm的速度从点A出发向C运动，到点C停止运动，点Q在射线AM上运动，且，当点P的运动时间为_________秒时，△ABC才能和△PQA全等．

17．(本题3分)如图所示的网格是正方形网格，点A，B，C，D均落在格点上，则∠BAD+∠ADC=_____．

18．(本题3分)如图，小明想测量池塘两端A，B间的距离，为了安全起见，小明借助全等三角形的知识．用了这样一个间接测量A，B间的距离方法：在地上取一点可以直接到达A点和B点的点C，测得长20m，长为20m，在的延长线上找一点D，使得长为20m，在的延长线上找一点E，使得长为20m，又测得此时D和E的距离为25m，根据小明的数据，可知A，B之间的距离为________m．

19．(本题3分)工人师傅常常利用角尺构造全等三角形的方法来平分一个角．如图，在的两边、上分别在取，移动角尺，使角尺两边相同的刻度分别与点、重合，这时过角尺顶点的射线就是的平分线．利用所学知识可知他构造全等三角形的依据是________．

20．(本题3分)如图，正方形ABCD的边长为4，点E、F分别在边AB、BC上，∠EDF＝45°，当AE＝a，CF＝b时，EF＝_______（用含a、b的式子表示）．


三、解答题(共40分)
21．(本题8分)如图，AB＝AC，直线l过点A，BM⊥直线l，CN⊥直线l，垂足分别为M、N，且BM＝AN．

(1)求证△AMB≌△CNA；
(2)求证∠BAC＝90°．
22．(本题8分)如图，在四边形ABCD中，点E为对角线BD上一点，∠A=∠BEC，∠ABD=∠BCE，且AD=BE．

(1)证明：①；②；
(2)若BC=15，AD=6，请求出DE的长度．
23．(本题8分)如图，，，，求证：．

24．(本题8分)阅读下列材料，完成相应任务．
数学活动课上，老师提出了如下问题：
如图1，已知中，是边上的中线．

求证：．
智慧小组的证法如下：
证明：如图2，延长至，使，

∵是边上的中线∴
在和中
∴（依据一）∴
在中，（依据二）
∴．
任务一：上述证明过程中的“依据1”和“依据2”分别是指：
依据1：______________________________________________；
依据2：______________________________________________．
归纳总结：上述方法是通过延长中线，使，构造了一对全等三角形，将，，转化到一个三角形中，进而解决问题，这种方法叫做“倍长中线法”．“倍长中线法”多用于构造全等三角形和证明边之间的关系．
任务二：如图3，，，则的取值范围是_____________；

任务三：如图4，在图3的基础上，分别以和为边作等腰直角三角形，在中，，；中，，．连接．试探究与的数量关系，并说明理由．

25．(本题8分)如图，AC平分，垂足分别为B，D．

(1)求证：；
(2)若，求四边形ABCD的面积．

参考答案：
1．C
【分析】带1、3去，只有两角，没有完整边不能确定三角形，带1、2或2、3去，只有一角，没有完整边，不能确定三角形，带2、4去，有一角，可以延长边还原出原三角形，带3、4可以用“角边角”确定三角形，带1、4可以用“角边角”确定三角形．即可得出答案
【详解】解：带1、3去，只有两角，没有完整边不能确定三角形，带1、2或2、3去，只有一角，不能确定三角形，带2、4去，有一角，可以延长边还原出原三角形，带3、4可以用“角边角”确定三角形，带1、4可以用“角边角”确定三角形，所以A、B、D不符合题意，C符合题，
故选：C．
【点睛】本题考查了全等三角形判定的应用；确定一个三角形的大小、形状，可以用全等三角形的几种判定方法．做题时要根据实际问题找条件．
2．D
【分析】根据全等三角形的判定方法判断即可；
【详解】解：A．两条直角边对应相等的两个直角三角形全等；可由（SAS）判断，正确；
B．一锐角和斜边对应相等的两个直角三角形全等；可由（AAS）判断，正确；
C．斜边和一直角边对应相等的两个直角三角形全等；可由（HL）判断，正确；
D．有两边相等的两个直角三角形无法判定边的对应相等关系，故不一定全等；选项错误，符合题意；
故选： D．
【点睛】本题考查了全等三角形的判定方法；熟练掌握（SSS）、（SAS）、（AAS）、（ASA）、（HL）的判定条件是解题关键．
3．C
【分析】由可证得，继而证明，由全等三角形对应角相等得到，最后由三角形的外角性质解答即可．
【详解】解：


，，


，

故选：C．
【点睛】本题考查全等三角形的判定与性质、三角形的外角性质等知识，是重要考点，掌握相关知识是解题关键．
4．A
【分析】由图示可知BD为公共边，若想用“HL”判定证明和全等，必须添加AD=CB．
【详解】解：在和中

∴
故选A
【点睛】此题主要考查学生对全等三角形判定定理（HL）的理解和掌握，此题难度不大，属于基础题．
5．D
【分析】利用同角的余角相等求出∠A＝∠2，再利用“角角边”证明△ABC和△CDE全等，根据全等三角形对应边相等、对应角相等，即可解答．
【详解】∵∠B＝∠E＝90°，
∴∠A+∠1＝90°，∠D+∠2＝90°，
∵AC⊥CD，
∴∠1+∠2＝90°，故D错误；
∴∠A＝∠2，故B正确；
∴∠A+∠D＝90°，故A正确；
在△ABC和△CED中，
，
∴△ABC≌△CED（AAS），
故C正确；
故选：D．
【点睛】考查了全等三角形的判定与性质，等角的余角相等的性质，解题关键是熟练掌握三角形全等的判定方法并确定出全等的条件∠A=∠2．
6．C
【分析】延长AD至点E，使得DE＝AD，可证△ABD≌△CDE，可得AB＝CE，AD＝DE，在△ACE中，根据三角形三边关系即可求得AE的取值范围，从而得到的取值范围．
【详解】如图，延长AD至点E，使得DE＝AD，

∵是边上的中线，
∴，
在△ABD和△CDE中，
，
∴△ABD△CDE（SAS），
∴AB＝CE=5，AD＝DE，
∵△ACE中，AC-CE＜AE＜AC+CE，
∴4＜AE＜14，
∴2＜AD＜7．
故选：C．
【点睛】本题主要考查倍长中线法解题，能够做出辅助线证出三角形全等再结合三角形三边关系是解题关键．
7．D
【分析】利用三角形内角和定理求出∠BAC=112°，利用全等三角形的性质证明∠BED=∠BAD即可解决问题．
【详解】解：∵∠ABC=30°，∠C=38°，
∴∠BAC=112°，
在△BMA和△BME中，
．
∴△BMA≌△BME（ASA），
∴BA=BE，
在△BDA和△BDE中，
，
∴△BDA≌△BDE（SAS），
∴∠BED=∠BAD=112°，
∴∠CED=68°，
∴∠CDE=180°-∠C-∠CED=74°，
故选：D．
【点睛】本题考查三角形内角和定理，全等三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．
8．D
【分析】根据OB平分∠AOC得∠AOB=∠BOC，又因为OE是公共边，根据全等三角形的判断即可得出结果．
【详解】解：∵OB平分∠AOC
∴∠AOB=∠BOC
当△DOE≌△FOE时，可得以下结论：
OD=OF，DE=EF，∠ODE=∠OFE，∠OED=∠OEF．
A答案中OD与OE不是△DOE≌△FOE的对应边，A不正确；
B答案中OE与OF不是△DOE≌△FOE的对应边，B不正确；
C答案中，∠ODE与∠OED不是△DOE≌△FOE的对应角，C不正确；
D答案中，若∠ODE=∠OFE，
在△DOE和△FOE中，

∴△DOE≌△FOE（AAS）
∴D答案正确．
故选：D．
【点睛】本题考查三角形全等的判断，理解全等图形中边和角的对应关系是解题的关键．
9．A
【分析】先证明△ADF≌△ABF，得∠ADF=∠ABF，再根据等角的余角相等，得2∠1=∠DFE，便可判断（1）的正误；当△ABC不是等腰直角三角形时，∠C≠45°，则∠C≠∠CBE，此时BE≠CE，便可判断（2）的正误；证明∠ABE=∠C=∠ADF，得DFBC，便可判断（4）的正确；过D点作DM⊥BC于点M，过点F作FN⊥BC于点N，则DM=FN，假设CD=DB,可得△CDM≌△FBN，当∠C≠45°，得CD≠BF，便可判断（3）的正误．
【详解】解：（1）在△ADF和△ABF中，
，
∴△ADF≌△ABF（SAS），
∴∠ADF=∠ABF，
∵∠ABF+∠BAE=∠ADF+∠DFE=90°，
∴∠BAE=∠DFE，
∵∠1=∠2，
∴2∠1=∠DFE，
故（1）错误；
（2）当△ABC不是等腰直角三角形时，∠C≠45°，
则∠C≠∠CBE，
此时BE≠CE，
故（2）错误；
（4）∵△ADF≌△ABF，
∴∠ABF=∠ADF，
∵AB⊥BC，BE⊥AC，
∴∠ABE+∠CBE=∠BCE+∠C=90°，
∴∠ABE=∠C，
∴∠ADF=∠C，
∴DFBC
故（4）正确；
（3） DFBC，
过D点作DM⊥BC于点M，过点F作FN⊥BC于点N，则DM=FN，

若，
∵∠C+∠CBF=∠C+∠CDM=90°，
∴∠CDM=∠FBN，
∴△CDM≌△FBN（AAS），
，
则
此时
当△ABC不是等腰直角三角形时，∠C≠45°，△CDM与△FBN不全等，
∴CDFB，
∵△ADF≌△ABF，
∴DF=BF．
∴BF=DFCD，
故（3）不正确；
综上所述，正确的有（4），共1个；
故选：A．
【点睛】本题考查了等腰直角三角形的性质、全等三角形的判定．解题的关键是掌握三角形的全等的判定定理．
10．D
【分析】根据题目给的条件可知道直角边和直角，因为需用“HL”的方法判定≌，故只能添上斜边这一条件，即可解答．
【详解】解：∵，，
∴添加条件，根据“HL”即可判定≌；或添加条件，也可得出，根据“HL”即可判定≌，故D正确．
故选：D．
【点睛】本题主要考查了利用“HL”判定三角形全等，掌握三角形全等的判定是解题的关键．
11．（答案不唯一）
【分析】两个三角形全等已具备的条件是：，，根据三角形全等的判定方法即可确定添加的条件．
【详解】解：添加的条件是，
，，
，
，
，
，
在和中，
，
．
故答案为：（答案不唯一）．
【点睛】本题考查了全等三角形的判定，掌握全等三角形的判定定理是解决问题的关键．
12．1
【分析】先证明△ACD≌△CBE，再求出DE的长，解决问题．
【详解】解：∵BE⊥CE于E，AD⊥CE于D
∴
∵
∴
∵
∴
∴，
∴．
故答案为：1
【点睛】此题考查三角形全等的判定和性质，掌握再全等三角形的判定和性质是解题的关键．
13．
【分析】作，交于，作，交于．通过平行线的性质证明，，，即可求出．
【详解】解：作，交于，作，交于，

是的中线，
，
，，
，
，
，
，
，
，
在和中，
，
，
，，
，
，
，
，
故答案为：．
【点睛】本题考查三角形的面积，三角形全等，平行线的性质，等高模型等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．
14．10或20
【分析】分两种情况：①当AP=BC=10时；②当AP=CA=20时；由HL证明Rt△ABC≌Rt△PQA（HL）；即可得出结果．
【详解】解：∵AX⊥AC，
∴∠PAQ=90°，
∴∠C=∠PAQ=90°，
分两种情况：
①当AP=BC=10时，
在Rt△ABC和Rt△QPA中，
，
∴Rt△ABC≌Rt△QPA（HL）；
②当AP=CA=20时，
在△ABC和△PQA中，
，
∴Rt△ABC≌Rt△PQA（HL）；
综上所述：当点P运动到AP=10或20时，△ABC与△APQ全等；
故答案为：10或20．
【点睛】本题考查了直角三角形全等的判定方法；熟练掌握直角三角形全等的判定方法，本题需要分类讨论，难度适中．
15．225°
【分析】首先判定△ABC≌△AEF，△ABD≌△AEH，可得∠5=∠BCA，∠4=∠BDA，然后可得∠1+∠5=∠1+∠BCA=90°，∠2+∠4=∠2+∠BDA=90°，即可求得∠1+∠2+∠3+∠4+∠5的值．
【详解】解：如图所示：

在△ABC和△AEF中，
∴△ABC≌△AEF（SAS），
∴∠5=∠BCA，
∴∠1+∠5=∠1+∠BCA=90°，
在Rt△ABD和Rt△AEH中，
∴Rt△ABD≌Rt△AEH（HL），
∴∠4=∠BDA，
∴∠2+∠4=∠2+∠BDA=90°，
∵∠3=45°，
∴∠1+∠2+∠3+∠4+∠5=90°+90°+45°=225°．
故答案为：225°．
【点睛】此题主要考查了全等三角形的判定和性质，关键是掌握全等三角形的性质：全等三角形对应角相等即可求解．
16．2或4##4或2
【分析】据全等三角形的判定HL定理分AP=BC和AP=AC解答即可．
【详解】解：设点P的运动时间为t秒，
∵，，
∴当AP=BC=4cm，时，Rt△QPA≌Rt△ABC（HL），
∴t=4÷2=2秒；
当AP=AC=8cm，时，Rt△PQA≌Rt△ABC（HL），
∴t=8÷2=4秒，
综上，当点P的运动时间为2或4秒时，△ABC才能和△PQA全等．
故答案为：2或4．
【点睛】本题考查全等三角形的判定，熟练掌握证明直角三角形全等的HL定理，利用分类讨论思想是解答的关键．
17．##度
【分析】证明△DCE≌△ABD（SAS），得∠CDE=∠DAB，根据同角的余角相等和三角形的内角和可得结论．
【详解】解：如图，设AB与CD相交于点F，

在△DCE和△ABD中，
∵，
∴△DCE≌△ABD（SAS），
∴∠CDE=∠DAB，
∵∠CDE+∠ADC=∠ADC+∠DAB=90°，
∴∠AFD=90°，
∴∠BAC+∠ACD=90°，
故答案为：90度．
【点睛】本题网格型问题，考查了三角形全等的性质和判定及直角三角形各角的关系，本题构建全等三角形是关键．
18．25
【分析】由题意知AC＝DC，BC＝EC，根据∠ACB＝∠DCE即可证明△ABC≌△DEC，即可得AB＝DE，即可解题．
【详解】解：由题意知AC＝DC，BC＝EC，且∠ACB＝∠DCE，
在△ABC和△DEC中，
，
∴△ABC≌△DEC（SAS），
∴DE＝AB，
∵DE＝25m，
∴AB＝25m，
故答案为：25．
【点睛】本题考查了全等三角形在实际生活中的应用，考查了全等三角形对应边相等的性质，本题中求证△ABC≌△DEC是解题的关键．
19．SSS
【分析】根据全等三角形的判定定理SSS推出△COM≌△DOM，根据全等三角形的性质得出∠COM=∠DOM，根据角平分线的定义得出答案即可．
【详解】解：在△COM和△DOM中，
.
∴△COM≌△DOM（SSS），
∴∠COM=∠DOM，
即OM是∠AOB的平分线，
故答案为：SSS．
【点睛】本题考查了全等三角形的判定定理和性质定理，能熟记全等三角形的判定定理是解此题的关键．
20．a＋b##b＋a
【分析】延长FC到M，使CM＝AE，连接DM，通过SAS可证明△ADE≌△CDM，得DE＝DM，∠ADE＝∠CDM，再通过SAS证明△DEF≌△DMF，从而有EF＝MF＝a＋b．
【详解】解：延长FC到M，使CM＝AE，连接DM，

∵四边形ABCD是正方形，
∴AD＝CD，∠A＝∠DCM＝90°，
在△ADE和△CDM中，，
∴△ADE≌△CDM（SAS），
∴DE＝DM，∠ADE＝∠CDM，
∵∠EDF＝45°，
∴∠ADE＋∠FDC＝45°，
∴∠CDM＋∠FDC＝45°，
∴∠FDM＝∠EDF＝45°，
在△DEF与△DMF中，，
∴△DEF≌△DMF（SAS），
∴EF＝MF＝a＋b，
故答案为：a＋b．
【点睛】本题主要考查了全等三角形的判定与性质，作辅助线构造全等三角形是解题的关键．
21．(1)证明见解析
(2)证明见解析

【分析】（1）由题意知∠AMB＝∠CNA＝90°，证明即可；
（2）由，可知∠BAM＝∠ACN，根据∠CAN+∠ACN＝90°，可得∠CAN+∠BAM＝90°，进而结论得证．
【详解】（1）证明：∵BM⊥直线l，CN⊥直线l，
∴∠AMB＝∠CNA＝90°，
在和中，
∵，
∴．
（2）证明：∵，
∴∠BAM＝∠ACN，
∵∠CAN+∠ACN＝90°，
∴∠CAN+∠BAM＝90°，
∴．
【点睛】本题考查了全等三角形的判定与性质以及直角三角形的性质．掌握全等三角形的判定定理和性质定理是解题的关键．
22．(1)①证明见解析；②证明见解析
(2)9

【分析】（1）①由ASA证明全等即可，②由①可证明；
（2）由△ABD≌△ECB可证DE=BD-BE=15-6=9．
【详解】（1）解：证明：①
在△ABD和△ECB中，
，
∴△ABD≌△ECB（ASA），
② 由①得：△ABD≌△ECB
∴∠ADB＝∠EBC，
∴AD∥BC ；
（2）∵△ABD≌△ECB，BC=15，AD=6，
∴BD＝BC=15，BE=AD=6，
∴DE=BD-BE=15-6=9．
【点睛】本题考查了全等三角形的判定与性质、平行线的判定等知识，证明△ABD≌△ECB是解题的关键．
23．见解析
【分析】根据，可得，进而根据SAS证明即可．
【详解】证明：∵，
∴，
∴，
在与中，
，
（SAS）．
【点睛】本题考查了全等三角形的判定，掌握全等三角形的判定定理是解题的关键．
24．任务一：依据1：两边和它们的夹角分别相等的两个三角形全等（或“边角边”或“SAS”）；依据2：三角形两边的和大于第三边；任务二：；任务三：EF=2AD，见解析
【分析】任务一：依据1：根据全等的判定方法判断即可；
依据2：根据三角形三边关系判断；
任务二：可根据任务一的方法直接证明即可；
任务三：根据任务一的方法，延长中线构造全等三角形证明线段关系即可．
【详解】解：任务一：
依据1：两边和它们的夹角分别相等的两个三角形全等（或“边角边”或“SAS”）；
依据2：三角形两边的和大于第三边．
任务二：
任务三：EF=2AD．理由如下：
如图延长AD至G，使DG=AD，

∵AD是BC边上的中线
∴BD=CD
在△ABD和△CGD中
∴△ABD≌△CGD
∴AB=CG，∠ABD=∠GCD
又∵AB=AE
∴AE=CG
在△ABC中，∠ABC+∠BAC+∠ACB=180°，
∴∠GCD+∠BAC+∠ACB=180°
又∵∠BAE=90°，∠CAF=90°
∴∠EAF+∠BAC=360°-（∠BAE+∠CAF）=180°
∴∠EAF=∠GCD
在△EAF和△GCA中

∴△EAF≌△GCA
∴EF=AG
∴EF=2AD．
【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质，倍长中线法，构造全等三角形是解本题的关键．
25．(1)见解析
(2)12

【分析】（1）由角平分线的定义和垂直的定义求出，结合已知条件，利用“AAS”即可求证；
（2）由全等三角形的性质得，根据三角形的面积公式求出，再根据四边形ABCD的面积求解即可．
【详解】（1） AC平分，
，
，
；
（2），，
，
，
，
四边形ABCD的面积．
【点睛】本题考查全等三角形的判定和性质，角平分线的定义，熟练掌握它们是解题的关键．