专题19 圆 山东省2023年中考数学一轮复习专题训练

这是一份专题19 圆 山东省2023年中考数学一轮复习专题训练，共41页。试卷主要包含了单选题，填空题，综合题等内容，欢迎下载使用。
1．（2022·济宁）已知圆锥的母线长8cm，底面圆的直径6cm，则这个圆锥的侧面积是（ ）
A．96πcm2B．48πcm2C．33πcm2D．24πcm2
2．（2022·枣庄）将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A，B的读数分别为86°，30°，则∠ACB的度数是（ ）
A．28°B．30°C．36°D．56°
3．（2022·聊城）如图，AB，CD是⊙O的弦，延长AB，CD相交于点P．已知∠P=30°，∠AOC=80°，则BD的度数是（ ）
A．30°B．25°C．20°D．10°
4．（2022·东营）用一张半圆形铁皮，围成一个底面半径为4cm的圆锥形工件的侧面（接缝忽略不计），则圆锥的母线长为（ ）
A．4cmB．8cmC．12cmD．16cm
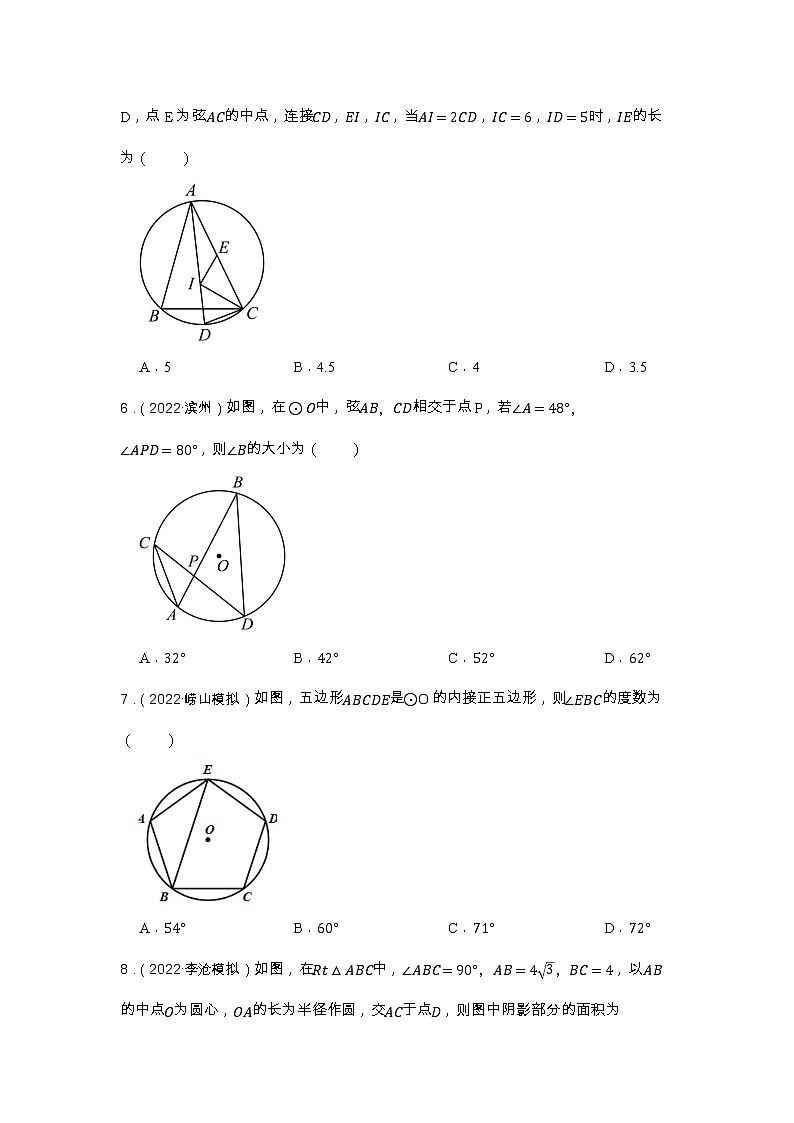
5．（2022·泰安）如图，点I为的△ABC内心，连接AI并延长交△ABC的外接圆于点D，点E为弦AC的中点，连接CD，EI，IC，当AI=2CD，IC=6，ID=5时，IE的长为（ ）
A．5B．4.5C．4D．3.5
6．（2022·滨州）如图，在⊙O中，弦AB，CD相交于点P，若∠A=48°，∠APD=80°，则∠B的大小为（ ）
A．32°B．42°C．52°D．62°
7．（2022·崂山模拟）如图，五边形ABCDE是⊙O的内接正五边形，则∠EBC的度数为（ ）
A．54°B．60°C．71°D．72°
8．（2022·李沧模拟）如图，在Rt△ABC中，∠ABC=90°，AB=43，BC=4，以AB的中点O为圆心，OA的长为半径作圆，交AC于点D，则图中阴影部分的面积为（ ）
A．53−2πB．53+2πC．43−πD．43+π
9．（2022·青岛模拟）如图，BD是⊙O的切线，∠BCE=32°，则∠D=（ ）
A．32°B．29°C．26°D．28°
10．（2022·兰山模拟）如图，正方形ABCD的边长为4，点E是边BC上一点，且BE=3，以点A为圆心，3为半径的圆分别交AB、AD于点F、G，DF与AE交于点H，并与圆A交于点K，连接HG、CH，给出下列4个结论，其中正确的结论有（ ）
①H是FK的中点；②S△AHG：S△DHC=9：16；③△HGD≌△HEC；④DK=75．
A．①③④B．①②③C．②③D．①②④
二、填空题
11．（2022·济宁）如图，点A，C，D，B在⊙O上，AC＝BC，∠ACB＝90°．若CD＝a，tan∠CBD＝13，则AD的长是 ．
12．（2022·日照）一圆形玻璃镜面损坏了一部分，为得到同样大小的镜面，工人师傅用直角尺作如图所示的测量，测得AB=12cm，BC=5cm，则圆形镜面的半径为 ．
13．（2022·菏泽）如图，等腰Rt△ABC中，AB=AC=2，以A为圆心，以AB为半径作BDC﹔以BC为直径作CAB．则图中阴影部分的面积是 ．（结果保留π）
14．（2022·聊城）如图，线段AB=2，以AB为直径画半圆，圆心为A1，以AA1为直径画半圆①；取A1B的中点A2，以A1A2为直径画半圆②；取A2B的中点A3，以A2A3为直径画半圆③…按照这样的规律画下去，大半圆内部依次画出的8个小半圆的弧长之和为 ．
15．（2022·崂山模拟）如图，在⊙O中，O为圆心，AB为直径，D为圆上一点，AB=2，∠DAB=30°，则阴影部分面积为 ；
16．（2022·聊城）若一个圆锥体的底面积是其表面积的14，则其侧面展开图圆心角的度数为 ．
17．（2022·李沧模拟）如图，在△ABC中，∠ACB=90°，AC=12，BC=5，将△ABC绕点C顺时针旋转90°得到ΔA'B'C，P为线段A'B'上的动点，以P为圆心、PA'为半径作⊙P，当⊙P与△ABC的边相切时，⊙P的半径的长为 ．
18．（2022·诸城模拟）如图，在过点P作直线a的垂线时，小颖先将一圆形透明纸片对折得到折痕AB，然后让端点A与点P重合，端点B落在直线a上，标出直线a与圆形纸片的交点C，连接AC，则AC⊥a．她的作图依据是 ．
19．（2022·惠民模拟）如图，将半径为2，圆心角为90°的扇形ABC绕A点逆时针旋转至点B的对应点点D落在弧AC上，则阴影部分的面积为 ．
20．（2022·沂南模拟）如图1是一张圆形纸片，小明同学进行了如下连续操作：
（1）将圆形纸片左右对折，上下对折，得到折痕AB与CD互相垂直，垂足为点M，如图2．
（2）将圆形纸片沿EF折叠，使BM两点重合，折痕EF与AB相交于N，连接AE、AF、BE、BF，如图3．小明得到了以下结论，其中正确的是 （只填写序号）．
①AE>EF；②∠EBF=120°；③CE=13CB；④四边形MEBF为菱形．
三、综合题
21．（2022·济宁）如图，在矩形ABCD中，以AB的中点O为圆心，以OA为半径作半圆，连接OD交半圆于点E，在BE上取点F，使BE=AF，连接BF，DF．
（1）求证：DF与半圆相切；
（2）如果AB＝10，BF＝6，求矩形ABCD的面积．
22．（2022·菏泽）如图，在△ABC中，以AB为直径作⊙O交AC、BC于点D、E，且D是AC的中点，过点D作DG⊥BC于点G，交BA的延长线于点H．
（1）求证：直线HG是⊙O的切线；
（2）若HA=3，csB=25，求CG的长．
23．（2022·济南）已知：如图，AB为⊙O的直径，CD与⊙O相切于点C，交AB延长线于点D，连接AC，BC，∠D＝30°，CE平分∠ACB交⊙O于点E，过点B作BF⊥CE，垂足为F．
（1）求证：CA＝CD；
（2）若AB＝12，求线段BF的长．
24．（2022·聊城）如图，点O是△ABC的边AC上一点，以点O为圆心，OA为半径作⊙O，与BC相切于点E，交AB于点D，连接OE，连接OD并延长交CB的延长线于点F，∠AOD=∠EOD．
（1）连接AF，求证：AF是⊙O的切线；
（2）若FC=10，AC=6，求FD的长．
25．（2022·潍坊）筒车是我国古代利用水力驱动的灌溉工具，车轮缚以竹简，旋转时低则舀水，高则泻水．如图，水力驱动筒车按逆时针方向转动，竹筒把水引至A处，水沿射线AD方向泻至水渠DE，水渠DE所在直线与水面PQ平行；设筒车为⊙O，⊙O与直线PQ交于P，Q两点，与直线DE交于B，C两点，恰有AD2=BD⋅CD，连接AB，AC．
（1）求证：AD为⊙O的切线；
（2）筒车的半径为3m，AC=BC，∠C=30°．当水面上升，A，O，Q三点恰好共线时，求筒车在水面下的最大深度（精确到0.1m，参考值：2≈1.4，3≈1.7）．
26．（2022·威海）如图，四边形ABCD是⊙O的内接四边形，连接AC，BD，延长CD至点E．
（1）若AB＝AC，求证：∠ADB＝∠ADE；
（2）若BC＝3，⊙O的半径为2，求sin∠BAC．
27．（2022·高唐模拟）如图，在菱形ABCD中，对角线AC，BD交于点O，∠BAO=30°，AC=8．过点O作OH⊥AB于点H，以点O为圆心，OH为半径的半圆交AC于点M．
（1）求图中阴影部分的面积；
（2）点P是BD上的一个动点（点P不与点B，D重合），当PH+PM的值最小时，求PD的长度．
28．（2022·临沭模拟）如图，钝角△ABC中，AB=AC，⊙O为△ABC的外接圆，点D为优弧BC上一点（不与B，C重合），连接AD，CD，AD交BC于点E，△ACD的内心F恰好落在BC上．
（1）求证：AB∥CD；
（2）连接AF，求证：AB=BF；
（3）若BE=4，CE=5，求CF的长．
29．（2022·庆云模拟）如图，AB是⊙O的直径，点C在AB的延长线上，∠BDC=∠A，CE⊥AD，交AD的延长线于点E．
（1）求证：CD与⊙O相切：
（2）若CE=4，DE=2，求AD的长，
答案解析部分
1．【答案】D
【解析】【解答】解：底面直径为6cm，则底面周长=6π，
侧面面积=12×6π×8=24πcm2．
故答案为：D．
【分析】先求出底面周长=6π，再利用圆锥的侧面积公式计算求解即可。
2．【答案】A
【解析】【解答】设半圆圆心为O，连OA，OB，如图，
∵∠AOB＝86°−30°＝56°，
∴∠ACB＝12∠AOB＝12×56°＝28°．
故答案为：A．
【分析】先求出∠AOB＝86°−30°＝56°，再求解即可。
3．【答案】C
【解析】【解答】解：如图，连接OB，OD，AC，
∵∠AOC=80°，
∴∠OAC+∠OCA=100°，
∵∠P=30°，
∴∠PAO+∠PCO=50°，
∵OA=OB，OC=OD，
∴∠OBA=∠OAB，∠OCD=∠ODC，
∴∠OBA+∠ODC=50°，
∴∠BOA+∠COD=260°，
∴∠BOD=360°−80°−260°=20°．
∴BD的度数20°．
故答案为：C．
【分析】连接OB，OD，AC，根据圆周角定理和圆心角、弧、弦的关系定理解答即可。
4．【答案】B
【解析】【解答】解：设圆锥的母线长为l，
由题意得：2×4π=180×π⋅l180，
∴l=8cm，
故答案为：B．
【分析】利用圆锥的底面周长等于侧面的弧长列出方程求解即可。
5．【答案】C
【解析】【解答】解：延长ID到M，使DM=ID，连接CM．
∵I是△ABC的内心，
∴∠IAC=∠IAB，∠ICA=∠ICB，
∵∠DIC=∠IAC+∠ICA，∠DCI=∠BCD+∠ICB，
∴∠DIC=∠DCI，
∴DI=DC=DM，
∴∠ICM=90°，
∴CM=IM2−IC2=8，
∵AI=2CD=10，
∴AI=IM，
∵AE=EC，
∴IE是△ACM的中位线，
∴IE=12CM=4，
故答案为：C．
【分析】延长ID到M，使DM=ID，连接CM，先利用勾股定理求出CM的长，再证明IE是△ACM的中位线，即可得到IE=12CM=4。
6．【答案】A
【解析】【解答】解：∵∠C+∠A=∠APD，∠A=48°，∠APD=80°，
∴∠C=32°
∴∠B=∠C=32°
故答案为：A．
【分析】先利用三角形的外角的性质求出∠C=32°，再利用圆周角的性质可得∠B=∠C=32°。
7．【答案】D
【解析】【解答】解：∵五边形ABCDE是⊙O的内接正五边形，
∴∠A=∠ABC=15(5−2)×180°=108°，AB=AE，
∴∠ABE=∠AEB，
∴∠ABE=12(180°−∠A)=36°，
∴∠EBC=∠ABC−∠ABE=108°−36°=72°．
故答案为：D．
【分析】先根据正多边形内角和公式计算出∠EAB，再得出∠ABE=∠AEB，即可得解。
8．【答案】A
【解析】【解答】解：如图，连接BD，OD，过点O作OE⊥AD于E，
在Rt△ABC中，由由勾股定理，得
AC=AB2+BC2=(43)2+42=8，
∴sinA=BCAC=48=12，
∴∠A=30°，
∵OA=OD，
∴∠ADO=∠A=30°，
∴∠BOD=∠ADO+∠A =60°，
∵AB是半⊙O的直径，
∴∠ADB=90°，OA=12AB=12×43=23，
∴S扇形BOD=60π×(23)2360=2π，
∵S△ABC=12AB⋅BC=12AC⋅BD，
∴43×4=8BD，
∴BD=23，
在Rt△ABD中，由由勾股定理，得
AD=(43)2−(23)2=6，
∵OE⊥AD，
∴E是AD的中点，
∵O是AB的中点，
∴OE是△ABD的中位线，
∴OE=12BD=3，
∴S△AOD=12AD⋅OE=12×6×3=33，
∴S阴影=S△ABC-S扇形BOD-S△AOD=12AB⋅BC-2π-33
=12×43×4-2π-33
=83-2π-33
=53-2π，
故答案为：A．
【分析】连接BD，OD，过点O作OE⊥AD于E，在Rt△ABC中，由由勾股定理，得AC的值，由OA=OD，得出∠ADB=90°，OA=12AB=12×43=23，再利用S阴影=S△ABC-S扇形BOD-S△AOD求解即可。
9．【答案】C
【解析】【解答】∵BD是⊙O的切线，
∴∠OBD=90°，
∴∠BOD+∠D=90°，
∵∠BCE=32°，
∴∠BOE=2∠BCE=64°，
∴∠D=90°−64°=26°，
故答案为：C．
【分析】由切线的性质可得∠OBD=90°，利用直角三角形两锐角互余可得∠BOD+∠D=90°，根据圆周角定理可得∠BOE=2∠BCE=64°，从而求出∠D的度数；
10．【答案】D
【解析】【解答】①在ΔABE与ΔDAF中，
AD=AB∠DAF=∠ABEAF=BE
∴ΔABE≌ΔDAF （SAS），
∴∠AFD=∠AEB，
∴∠AFD+∠BAE=∠AEB+∠BAE＝90°，
∴AH⊥FK，
由垂径定理，得：FH=HK，
即H是FK的中点，故①符合题意；
③如图，
过H分别作HM⊥AD于M，HN⊥BC于N，
∵AB=4，BE=3，
∴AE=AB2+BE2=5，
∴∠BAE=∠HAF=∠AHM，
∴cs∠BAE=cs∠HAF=cs∠AHM，
∴HMAH=AHAF=ABAE=45，
∴AH=125，HM=4825，
∴HN=4−4825=5225，
即HM≠HN，
∵MN∥CD，
∴MD=CN，
∵HD=HM2+MD2，HC=HN2+CN2，
∴HC≠HD，
∴ΔHGD≌ΔHEC是错误的，故③不符合题意；
②过H分别作HT⊥CD于T，由③知，AM=AH2−HM2=3625，
∴DM=4−3625=6425，
∵MN∥CD，
∴MD=HT=6425，
∴S△AHGS△HCD=12AG·HM12CD·HT=916，
故②符合题意；
④由③知，
HF=AF2−AH2=95，
∴FK=2HF=185，
∴DK=DF-FK=75，故④符合题意．
故答案为：D．
【分析】利用正方形的性质、圆的性质及相似三角形的判定和性质逐项判断即可。
11．【答案】22a
【解析】【解答】解：如图，连接AB，设AD、BC交于点E，
∵∠ACB＝90°
∴AB是⊙O的直径，
∴∠ADB=90°，
∵ tan∠CBD＝13，
∴DEDB=13，
在Rt△DEB中，BE=DE2+DB2=10DE ，
∵CD=CD，
∴∠CBD=∠ACD，
∴tan∠CAD=13，
∴CEAC=13
设AC=m
则CE=13m，
∵ AC＝BC，
∴EB=23m，
∴DE=1010BE=21030m，
Rt△ACE中，AE=AC2+CE2=m2+(13m)2=103m，
∴AD=AE+ED=21030m+103m=2510m，
∵DB=DB，
∴∠ECD=∠EAB，
又∠CED=∠AEB，
∴△CED∽△AEB，
∴CDAB=CEAE=13m10m3=110，
∵CD=a，
∴AB=10a，
∵AC=BC=m，
∴AB=2m，
∴2m=10a，
解得m=5a，
∴AD=2510m=2510×5a=22a，
故答案为：22a．
【分析】先求出AB是⊙O的直径，再利用勾股定理，相似三角形的判定与性质求解即可。
12．【答案】132cm
【解析】【解答】解：连接AC，
∵∠ABC=90°，且∠ABC是圆周角，
∴AC是圆形镜面的直径，
由勾股定理得：AC=AB2+BC2=122+52=13(cm)，
所以圆形镜面的半径为132cm，
故答案为：132cm．
【分析】先求出AC是圆形镜面的直径，再利用勾股定理求出AC=13cm，最后求解即可。
13．【答案】π−2
【解析】【解答】解：∵等腰Rt△ABC中，AB=AC=2
∴BC=2
∴S扇形ACB=90π×2360=π2，S半圆CAB=12π×（1）2=π2，S△ABC=12×2×2=1；
所以阴影部分的面积＝S半圆CAB-S△ABC+S扇形ACB-S△ABC=π2−1+π2−1=π−2．
故答案为：π−2．
【分析】先求出BC=2，再利用扇形面积公式计算求解即可。
14．【答案】255256π或255π256
【解析】【解答】解：∵AB=2，
∴AA2=1，半圆①弧长为π×12=12π，
同理A1A2=12，半圆②弧长为π×122=(12)2π，
A2A3=14，半圆③弧长为π×142=(12)3π，
……
半圆⑧弧长为π×(12)72=(12)8π，
∴8个小半圆的弧长之和为12π+(12)2π+(12)3π+⋅⋅⋅+(12)8π=255256π．
故答案为：255256π．
【分析】由AB=2，得出半圆①弧长为π×12=12π，同理A1A2=12，半圆②弧长为π×122=(12)2π，同理A1A2=12，半圆②弧长为π×122=(12)2π，……半圆⑧弧长为π×(12)72=(12)8π，即可得出8个小半圆的弧长之和为12π+(12)2π+(12)3π+⋅⋅⋅+(12)8π=255256π。
15．【答案】34+π6
【解析】【解答】解：如图，过点O作OG⊥AD于G，连接OD，
在⊙O中，直径AB=2，∠DAB=30°
∴AO=BO=DO=1，
∴AG=DG=12AD，∠ODA=∠DAB=30°，
在Rt△AGO中，AO=1，∠DAB=30°，
∴GO=AO·sin∠DAB=1×12=12，
AG=AO·cs∠DAB=1×32=32，
∴AD=2AG=3，
∵∠DOB=∠ODA+∠OAD=60°，
∴S△AOD=12AD·OG=12×3×12=34，
S扇形BOD=60π×12360=π6，
∴S阴影=S△AOD+S扇形BOD=34+π6．
【分析】过点O作OG⊥AD于G，连接OD，则AO=BO=DO=1，先根据圆周角定理得出∠DOB=60°，进而得出∠DAB=30°，再根据勾股定理得出DH，最后根据阴影面积S△AOD+S扇形BOD计算即可。
16．【答案】120°或120度
【解析】【解答】解：设底面圆的半径为r，侧面展开扇形的半径为R，扇形的圆心角为n°．
由题意得S底面面积=πr2，
l底面周长=2πr，
∵个圆锥体的底面积是其表面积的14，
∴S扇形=3S底面面积=3πr2，
l扇形弧长=l底面周长=2πr．
由S扇形=12l扇形弧长×R得3πr2=12×2πr×R，
故R=3r．
由l扇形弧长=nπr180得：
2πr=nπ×3180，
解得n=120．
故答案为：120°．
【分析】设底面圆的半径为r，侧面展开扇形的半径为R，扇形的圆心角为n°，根据题意列出方程2πr=nπ×3180，求出n的值即可。
17．【答案】10213或15625
【解析】【解答】解：在△ABC中，∠ACB=90°，AC=12，BC=5，
在Rt△ABC中，由勾股定理：AB=AC2+BC2=13，
由旋转性质可知，A'B'=AB=13，B'C=BC=5，CA'=CA=12，
设⊙P的半径为r，
若⊙P与AC相切，如图，设切点为M，连接PM，
则PM⊥AC，且PM=PA'，∠A=∠A′，
∵PM⊥AC，A'C⊥AC，
∴PM∥CA'，
∴ΔBMP∽ΔB'CA'，
PMA'C=B'PB'A'即r12=13−r13，
∴r=15625．
若⊙P与AB相切，如图，延长PB'交AB于点N，
∵∠A=∠A′，∠B=∠B，
∴△ABC∽△A′BN，
∴ABA'B=ACA'N即1317=122r，
∴r=10213．
故答案为：10213或15625．
【分析】分两种情况求解：当⊙P与直线AC相切于点M时，当⊙P与AB相切于点N时，利用相似三角形的判定和性质求解即可。
18．【答案】直径所对的圆周角是直角
【解析】【解答】解：如图，作图依据是直径所对的圆周角是直角，
故答案为：直径所对的圆周角是直角．
【分析】根据“直径所对的圆周角是直角”可得答案。
19．【答案】3+13π
【解析】【解答】解：过A作AF⊥BD于点F，则∠AFB=90°，如图：
由旋转可知：扇形ABC和扇形ADE面积相等，AB=AD=BC=BD=2，
∴△ABD是等腰三角形，
∴∠ABF=60°，
∴∠BAF=30°，
∴BF=12AB=12×2=1，
由勾股定理得：AF=22−12=3，
∴阴影部分的面积为：S=S扇形ABC−(S扇形ABD−S△ABD)=90π×22360−(60π×2360−12×2×3)=3+13π。
故答案为：3+13π。
【分析】利用割补法列出算式S=S扇形ABC−(S扇形ABD−S△ABD)，再利用扇形的面积公式和三角形的面积公式求解即可。
20．【答案】②③④
【解析】【解答】解：根据垂径定理，BM垂直平分EF，
又∵纸片沿EF折叠，B、M两点重合，
∴BN=MN，
∴BM、EF互相垂直平分，
∴四边形MEBF是菱形，故④符合题意；
∴ME=MB=2MN，
∴∠MEN=30°，
∴∠EMN=90°−30°=60°，
∴∠EMF=120°，
∴∠EBF=120°，故②符合题意；
又∵AM=ME（都是半径），
∴∠AEM=∠EAM，
∴∠AEM=12∠EMN=12×60°=30°，
∴∠AEF=∠AEM+∠MEN=30°+30°=60°，
即∠EAF=12∠EBF，
同理可求∠AFE=60°，
∴∠EAF=60°，
∴△AEF是等边三角形，
∴AE=EF，故①不符合题意；
∵∠FME=∠EBF=120°，
∴∠EMB=60°，
∴∠CME=90°−60°=30°；
∴∠CME=13∠CMB，
∴CE=13CB；故③符合题意；
综合上述，正确的选项有②③④；
故答案为：②③④．
【分析】由折叠的性质以及直角三角形的性质证出∠EAF=60°，∠EBF=120°，可得出②正确；由等边三角形的判定即性质可得出①错误；由勾股定理及垂径定理可得出④正确；由圆周角定理及圆心角、弧的关系可得出③正确。
21．【答案】（1）证明：连接OF．
∵AE=EF，∴∠DOA=∠FOD.∵AO=FO，DO=DO，∴△DAO≅△DFO(SAS)∴∠DAO=∠DFO.∵四边形ABCD是矩形，∴∠DAO=90∘
∴∠DFO=90∘.∴DF与半圆相切.
（2）解：连接AF，∵AO=FO，∠DOA=∠DOF，∴DO⊥AF，∵AB为半圆的直径，∴∠AFB=90∘，∴BF⊥AF，∴DO//BF.∴∠AOD=∠ABF.∵∠OAD=∠AFB=90∘，∴△AOD∽△FBA∴AOBF=DOAB，∴56=DO10，∴DO=253，在RtΔAOD中，AD=DO2−AO2=(253)2−52=203.∴矩形ABCD的面积为203×10=2003.
【解析】【分析】（1）利用全等三角形的判定与性质求解即可；
（2）利用平行线的判定与性质，相似三角形的判定与性质，勾股定理计算求解即可。
22．【答案】（1）解：连接OD，
∵DG⊥BC，
∴∠BGH=90°，
∵D是AC的中点，AB为直径，
∴OD∥BC，
∴∠BGH=∠ODH=90°，
∴直线HG是⊙O的切线；
（2）解：由（1）得OD∥BC，
∴∠HBG=∠HOD，
∵cs∠HBG=25，
∴cs∠HOD=25，
设OD=OA=OB=r，
∵HA=3，
∴OH=3+r，
在Rt△HOD中，∠HDO=90°，
∴cs∠HOD=ODOH=r3+r=25，
解得r=2，
∴OD=OA=OB=2，OH=5，BH=7，
∵D是AC的中点，AB为直径，
∴BC=2OD=4，
∵∠BGH=∠ODH=90°，
∴△ODH∼△BGH，
∴OHBH=ODBG，即57=2BG，
∴BG=145，
∴CG=BC−BG=4−145=65．
【解析】【分析】（1）先求出 ∠BGH=90°， 再求出 ∠BGH=∠ODH=90°， 最后证明求解即可；
（2）利用锐角三角函数，相似三角形的判定与性质计算求解即可。
23．【答案】（1）证明：连接OC
∵CD与⊙O相切于点C，
∴OC⊥CD，
∴∠OCD=90°，
∵∠CDA=30°，
∴∠COB=90°−∠CDA=60°，
∵BC所对的圆周角为∠CAB，圆心角为∠COB，
∴∠CAB=12∠COB=30°，
∴∠CAD=∠CDA，
∴CA=CD．
（2）解：∵AB为直径，
∴∠ACB=90°，
在Rt△ABC中，∠CAB=30°，AB=12，
∴BC=12AB=6，
∵CE平分∠ACB，
∴∠ECB=12∠ACB=45°，
∵BF⊥CE，
∴∠CFB=90°，
∴BF=BC⋅sin45°=6×22=32．
【解析】【分析】（1）先求出 ∠OCD=90°， 再求出 ∠CAB=12∠COB=30°， 最后证明求解即可；
（2）先求出 BC=12AB=6， 再求出 ∠ECB=12∠ACB=45°， 最后利用锐角三角函数计算求解即可。
24．【答案】（1）证明：在△AOF和△EOF中，
OA=OE∠AOD=∠EODOF=OF，
∴△AOF≌△EOF（SAS），
∴∠OAF=∠OEF，
∵BC与⊙O相切，
∴OE⊥FC，
∴∠OAF=∠OEF=90°，
即OA⊥AF，
∵OA是⊙O的半径，
∴AF是⊙O的切线；
（2）解：在Rt△CAF中，∠CAF=90°，FC=10，AC=6，
∴AF=FC2−AC2=8，
∵BC与⊙O相切，AF是⊙O的切线
∴∠OEC＝∠FAC＝∠90°，
∵∠OCE=∠FCA，
∴△OEC∽△FAC，
∴EOAF=COCF，
设⊙O的半径为r，则r8=6−r10，
解得r=83，
在Rt△FAO中，∠FAO=90°，AF=8，AO=83，
∴OF=AF2+AO2=8310，
∴FD=OF−OD=8310−83，
即FD的长为8310−83．
【解析】【分析】（1）利用SAS证出△AOF≌△EOF，得出∠OAF=∠OEF，推出OA⊥AF，由OA是⊙O的半径，即可得出结论；
（2）在Rt△CAF中，∠CAF=90°，FC=10，AC=6，利用勾股定理得出AF的值，由BC与⊙O相切，AF是⊙O的切线，得出∠OEC＝∠FAC＝∠90°，再利用相似证出△OEC∽△FAC，得出EOAF=COCF，设⊙O的半径为r，则r8=6−r10，得出r的值，在Rt△FAO中，∠FAO=90°，AF=8，AO=83，利用勾股定理得出OF的值，从而得出FD的值，即可得出FD的长。
25．【答案】（1）证明：连接AO 并延长交⊙O 于M，连接BM，
∴AM为⊙O的直径，
∴∠ABM=90°，
∴∠BAM+∠AMB=90°，
∵AD2=BD⋅CD，
∴ADBD=CDAD，
又∵∠D=∠D，
∴ΔDAB∼ΔDCB，
∴∠DAB=∠DCA，
又∵∠BCA=∠BMA，
∴∠BAM+∠DAB=90°，
∴∠DAM=90°，
∴AD为⊙O的切线；
（2）解：如图所示，
∵AC=BC，∠C=30°，
∴∠CAB=∠CBA=12(180°−∠C)=12(180°−30°)=75°，
∵AQ 是⊙O的直径，
∴∠ABQ=∠APQ=90°，
∵∠C=30° ，
∴∠AQB=∠C=30° ，
∴∠BAQ=90°−∠AQB=60° ，
∴∠QAC=∠BAC−∠BAQ=75°−60°=15°，
∵PQ//BC，
∴BP=CQ，
∴∠QAC=∠BQP=15°，
∴∠PQA=∠BQP+∠BQA=15°+30°=45° ，
过O作OF⊥PQ交⊙O于F，
∴ΔOEQ为等腰直角三角形，
∵OQ=3，
∴OE=OQsin45°=3×22=322，
∴EF=OF−OE=3−322≈0.9(m)．
【解析】【分析】（1）连接AO 并延长交⊙O 于M，连接BM，利用直径所对的圆周角为直角得出∠BAM+∠AMB=90°，再说明ΔDAB∼ΔDCB，即可得出结论；
（2）由AQ 是⊙O的直径，得出∠ABQ=∠APQ=90°，再由PQ//BC，得出BP⌢=CQ⌢，证出ΔOEQ为等腰直角三角形，由OQ的值得出OE的值，即可得出答案。
26．【答案】（1）解：∵圆内接四边形外角等于内对角，四边形ABCD是圆的内接四边形，
∴∠ABC＝∠ADE，
∵AB=AC，
∴∠ABC＝∠ACB，
∵∠ADB＝∠ACB，
∴∠ADB＝∠ADE．
（2）解：如图，作直径BF，连接FC，
则∠BCF=90°，
∵圆的半径为2，BC=3，
∴BF=4，BC=3，∠BAC= ∠BFC，
∴sin∠BAC= sin∠BFC=BCBF=34．
【解析】【分析】（1）利用圆内接四边形的性质和角的运算及等量代换可得答案；
（2）作直径BF，连接FC，先求出BF=4，BC=3，∠BAC= ∠BFC，再利用正弦的定义求解即可。
27．【答案】（1）解：∵四边形ABCD是菱形，
∴AC⊥BD，OA=OC=4，
∵OH⊥AB，
∴∠AHO=90°，
∵∠OAH=30°，
∴∠AOH=60°，OH=12OA=2，AH=3OH=23，
∴S阴=S△AOH-S扇形OMH=12×2×2×3−60⋅π⋅22360=23−23π
（2）解：作点M关于BD的对称点M′，连接HM′交BD于P，连接PM，连接PM，此时PH+PM的值最小．
∵OH=OM′，
∴∠OHM′=∠OM′H，
∵∠AOH=∠OHM′+∠OM′H=60°，
设OP=m，则PM=2m，
∵PM2=OM2+OP2，
∴4m2=m2+22，
∴m=233，
∴PD=OD+OP=433+233=23．
【解析】【分析】（1）利用割补法求出阴影部分的面积即可；
（2）作点M关于BD的对称点M′，连接HM′交BD于P，连接PM，连接PM，此时PH+PM的值最小，设OP=m，则PM=2m，利用勾股定理可得4m2=m2+22，求出m的值，再利用线段的和差可得PD=OD+OP=433+233=23。
28．【答案】（1）证明：∵AB=AC，
∴AB=AC，
∴∠B=∠ACB，
∵F是△ACD的内心，
∴CF平分∠ACD，
∴∠ACB=∠DCB，
∴∠B=∠BCD，
∴AB∥CD；
（2）证明：∵F是△ACD的内心，
∴AF平分∠CAD，CF平分∠ACD，
∴∠DAF=∠CAF，∠ACB=∠DCB，
∵∠BAD=∠DCB，
∴∠BAD=∠ACB，
∴∠BAD+∠DAF=∠ACB+∠CAF，
即∠BAF=∠AFB，
∴AB=BF；
（3）解：由（2）知：∠BAE=∠ACB，又∵∠ABE=∠CBA，
∴△ABE∽△CBA，
∴ABBC=BEAB，
∴AB2=BE⋅BC=BE⋅（BE+CE）=4×（4+5）=36，
∴AB=6，
由（2）知：BF=AB=6，
∴CF=BC-BF=（BE+CE）-BF=（4+5）-6=3，
答：CF的长为3．
【解析】【分析】（1）先证明∠B=∠ACB，再结合∠ACB=∠DCB，可得∠B=∠BCD，从而可得AB//CD；
（2）利用角的运算和等量代换可得∠BAF=∠AFB，从而可得AB=BF；
（3）先证明△ABE∽△CBA，可得ABBC=BEAB，求出AB=6，再利用线段的和差可得CF的长。
29．【答案】（1）证明：连接OD，
∵AB为⊙O的直径，
∴∠ADB=90°，
即∠ODB+∠ADO=90°，
∵OA=OD，
∴∠ADO=∠A，
又∵∠BDC=∠A；
∴∠ODB+∠BDC=90°，
即∠ODC=90°
∴CD是⊙O切线.
（2）解：∵CE⊥AE，
∴∠E=∠ADB=90°，
∴DB // EC，
∴∠DCE=∠BDC，
∵∠BDC=∠A，
∴∠A=∠DCE，
∵∠E=∠E，
∴△AEC∽△CED，
∴CEDE=AECE，
∴CE2=DE⋅AE，
∴16=2(2+AD)，
∴AD=6．
【解析】【分析】（1）连接OD，先证明∠ODB+∠BDC=90°即∠ODC=90° ，从而可得CD是⊙O切线；
（2）先证明△AEC∽△CED可得CEDE=AECE，化简可得CE2=DE⋅AE，再将数据代入可得16=2(2+AD)，最后求出AD的长即可