冀教版数学七年级下册 9.3 三角形的角平分线、中线和高 课件+教案+练习

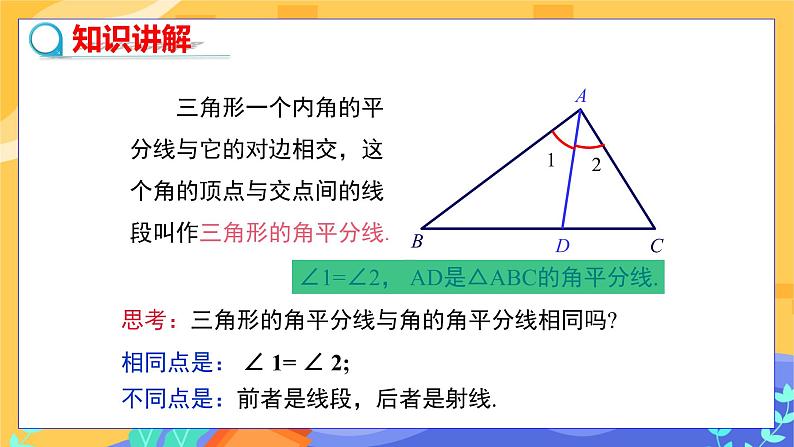
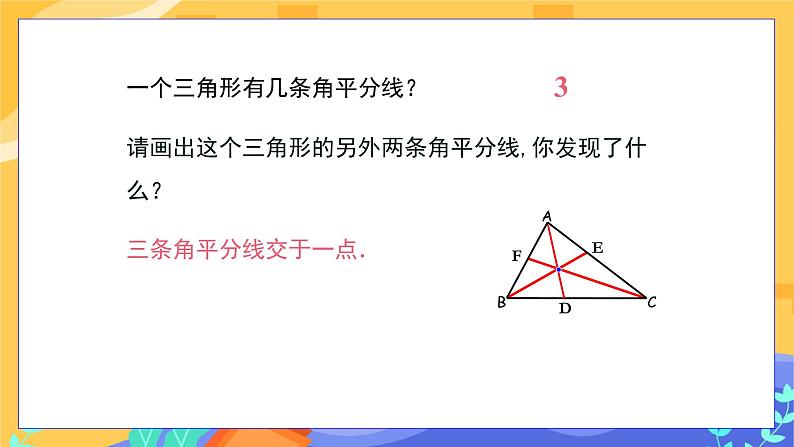
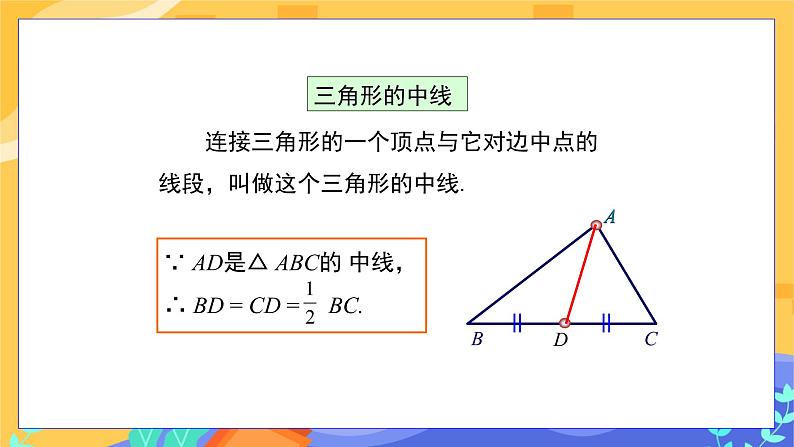
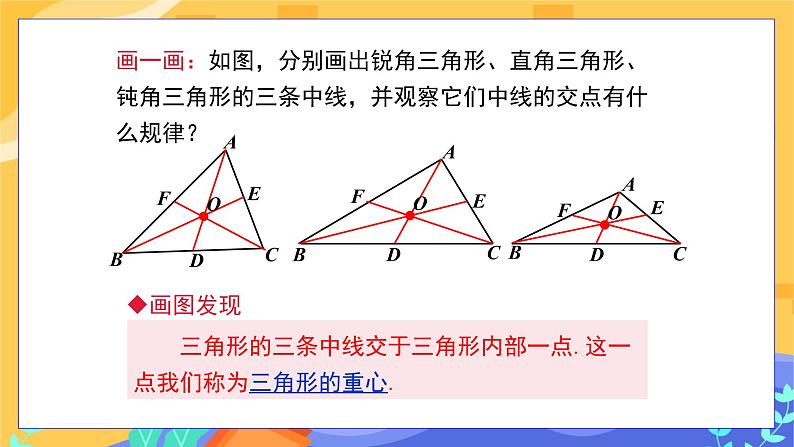
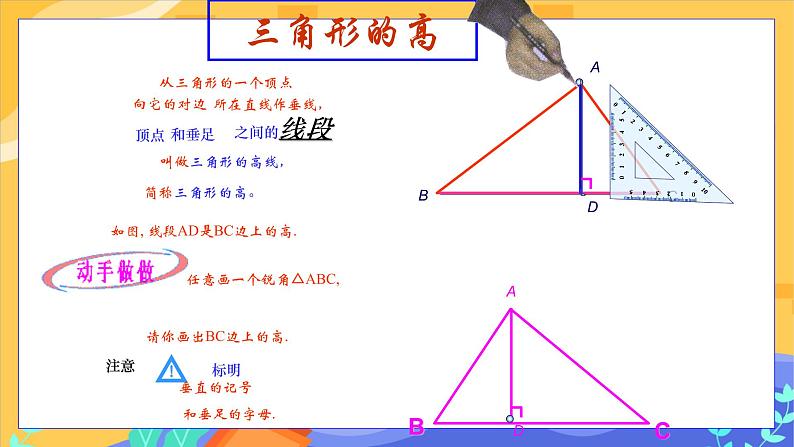
教学目标

1.理解并认识三角形的角平分线、中线和高.

2.会画任意三角形的角平分线、高、中线，了解三角形的重心.

教学重点难点

重点：理解三角形的高、中线、角平分线.

难点：三角形的重心的概念的理解.

教学过程

旧知回顾

1.上节课我们学习三角形按角分为哪几类？ 学生回顾思考，并举例回答：

（1）锐角三角形；  （2）直角三角形； （3）钝角三角形. 

2.试着做做： 如图，已知△ABC,

（1）画出∠A的平分线.

（2）画出边BC的中点，并与点A连接.

（3）过点A画出BC所在的直线的垂线. 

（回顾三角形三线的画法以及折纸的方法进行）

学生动手操作，然后进行展示.

探究新知

1.三角形的角平分线

定义：三角形一个内角的平分线与它的对边相交，这个角的顶点与交点间的线段叫做三角形的角平分线.

区分：三角形的角平分线和角平分线的区别和联系.

学生交流：

一个角的角平分线是一条射线，一个三角形的角平分线是一条线段，但它们都可以把这个角分成大小相等的两个角.

三角形的角平分线的几何语言：

∵AD是 △ ABC的角平分线，

∴∠ BAD ＝ ∠ CAD ＝  ∠BAC.

教师提出问题：一个三角形有几条角平分线？请画出这个三角形的另外两条角平分线,你发现了什么？

学生动手操作，得出答案：一个三角形有三条角平分线，三条角平分线交于一点.

2.三角形的中线

连接三角形的一个顶点与它对边中点的线段叫做这个三角形的中线.

几何语言：

∵ AD是△ABC的中线，

∴ BD＝CD＝BC.

请同学们认真观察，在这个三角形中，如果我知道AD是△ABC的中线，除了能够得出BD＝CD之外，还能有其他的相等关系吗？（把原三角形分成面积相等的两个三角形），为什么呢？ （找同学们边操作，边讲解“等底同高”）

分别画出锐角三角形、直角三角形、钝角三角形的三条中线，并观察它们中线的交点有什么规律？（学生动手操作）

学生得出结论：三角形的三条中线交于三角形内部一点，（师）这一点我们称为三角形的重心.

让学生拿出课前准备好的硬纸板，裁出一个三角形，通过画图找出它的重心，在重心处钻一个小孔，通过小孔系一条线将三角形的纸板吊起，三角形的纸板处于什么状态.（平衡状态）

３.三角形的高

三角形的一个顶点到它对边所在直线的垂线段叫做三角形的高线，简称三角形的高. 

几何语言：

∵ AD是△ ABC的高，

∴ ∠BDA＝∠CDA＝90°.

学生动手画：分别画出锐角三角形、直角三角形、钝角三角形的三条高，观察三条高有什么位置关系？

放手让学生操作，交流，自己发现规律.

师生总结：1.锐角三角形的三条高交于同一点，且三条高都在三角形的内部.2.直角三角形的三条高交于直角顶点.3.钝角三角形的三条高不相交于一点，但三条高所在直线交于一点.

课堂小结

布置作业

教材第111页习题A组、B组.

板书设计

9.3  三角形的角平分线、中线和高

1.三角形的角平分线

2.三角形的中线

3.三角形的高

4.三角形的重心