高考数学二轮复习专项分层特训命题点19统计与统计案例含答案

这是一份高考数学二轮复习专项分层特训命题点19统计与统计案例含答案，共12页。试卷主要包含了单项选择题，多项选择题，填空题等内容，欢迎下载使用。

一、单项选择题
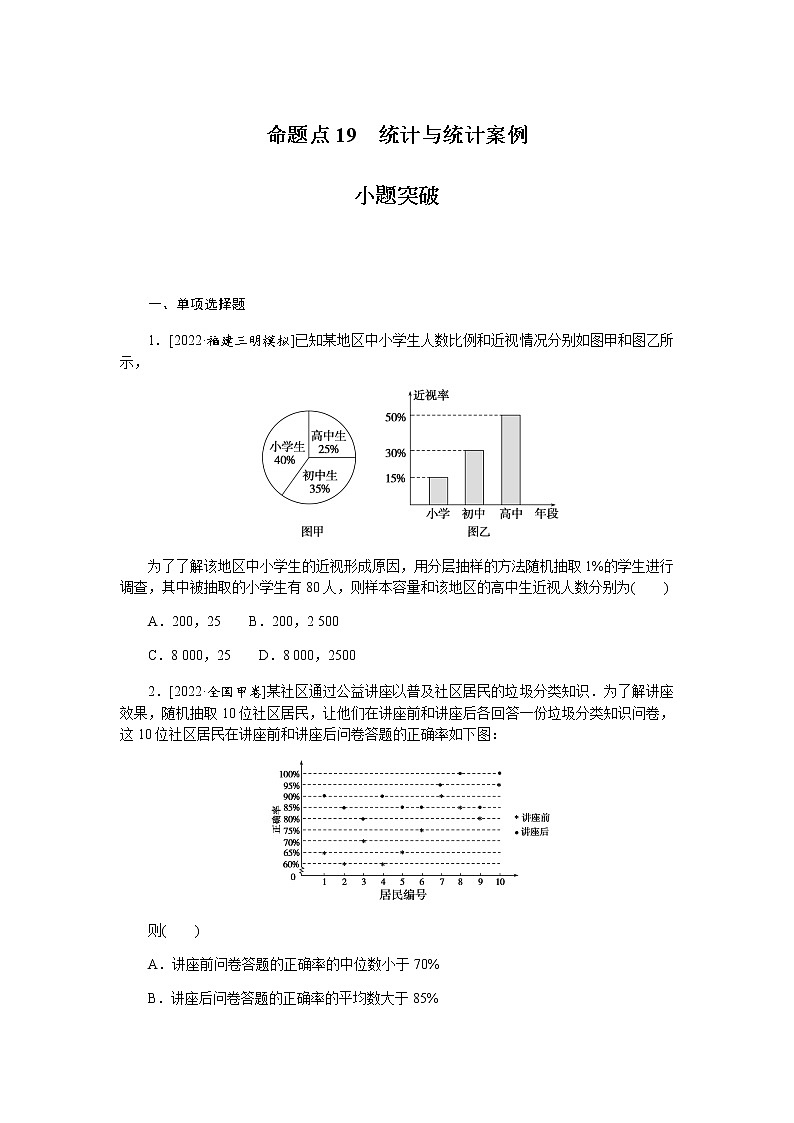
1．[2022·福建三明模拟]已知某地区中小学生人数比例和近视情况分别如图甲和图乙所示，
为了了解该地区中小学生的近视形成原因，用分层抽样的方法随机抽取1%的学生进行调查，其中被抽取的小学生有80人，则样本容量和该地区的高中生近视人数分别为( )
A．200，25 B．200，2 500
C．8 000，25 D．8 000，2500
2．[2022·全国甲卷]某社区通过公益讲座以普及社区居民的垃圾分类知识．为了解讲座效果，随机抽取10位社区居民，让他们在讲座前和讲座后各回答一份垃圾分类知识问卷，这10位社区居民在讲座前和讲座后问卷答题的正确率如下图：
则( )
A．讲座前问卷答题的正确率的中位数小于70%
B．讲座后问卷答题的正确率的平均数大于85%
C．讲座前问卷答题的正确率的标准差小于讲座后正确率的标准差
D．讲座后问卷答题的正确率的极差大于讲座前正确率的极差
3．[2022·福建龙岩一模]国外新冠肺炎疫情形势严峻，国内疫情传播风险加大，为了更好地抗击疫情，国内进一步加大新冠疫苗的接种力度．某制药企业对某种新冠疫苗开展临床接种试验，若使用该疫苗后的抗体呈阳性，则认为该新冠疫苗有效．该企业对参与试验的1 000名受试者的年龄和抗体情况进行统计，结果如下图表所示：
则下列结论正确的是( )
A．在受试者中，50岁以下的人数为700
B．在受试者中，抗体呈阳性的人数为800
C．受试者的平均年龄为45岁
D．受试者的疫苗有效率为80%
4．[2022·山东枣庄一模]下图是根据某班学生在一次数学考试中的成绩画出的频率分布直方图，则由直方图得到的25%分位数为( )
A．66.5 B．67
C．67.5 D．68
5．[2022·湖南岳阳三模]已知一组数据：x1，x2，x3的平均数是5，方差是4，则由2x1＋1，2x2＋1，2x3＋1和11 这四个数据组成的新数据组的方差是( )
A．16 B．14
C．12 D．11
6．[2022·湖南永州三模]某新能源汽车销售公司统计了某款汽车行驶里程x(单位：万千米)对应维修保养费用y(单位：万元)的四组数据，这四组数据如下表：
若用最小二乘法求得回归直线方程为 eq \(y,\s\up6(^)) ＝0.58x＋ eq \(a,\s\up6(^)) ，则估计该款汽车行驶里程为6万千米时的维修保养费是( )
A．3.34万元 B．3.62万元
C．3.82万元 D．4.02万元
7．[2022·山东青岛高三期末]通过随机询问某中学110名中学生是否爱好跳绳，得到如下列联表：
已知χ2＝ eq \f(n（ad－bc）2,（a＋b）（c＋d）（a＋c）（b＋d）) ，P(χ2≥10.828)＝0.001，根据小概率值α＝0.001的χ2独立性检验，以下结论正确的为( )
A．爱好跳绳与性别有关
B．爱好跳绳与性别有关，这个结论犯错误的概率不超过0.001
C．爱好跳绳与性别无关
D．爱好跳绳与性别无关，这个结论犯错误的概率不超过0.001
8．[2022·山东济宁二模]为研究变量x，y的相关关系，收集得到下面五个样本点(x，y)：
若由最小二乘法求得y关于x的回归直线方程为 eq \(y,\s\up6(^)) ＝－1.8x＋ eq \(a,\s\up6(^)) ，则据此计算残差为0的样本点是( )
A．(5，9) B．(6.5，8)
C．(7，6) D．(8，4)
二、多项选择题
9．[2021·新高考Ⅱ卷]下列统计量中，能度量样本x1，x2，…，xn的离散程度的是( )
A．样本x1，x2，…，xn的标准差
B．样本x1，x2，…，xn的中位数
C．样本x1，x2，…，xn的极差
D．样本x1，x2，…，xn的平均数
10．[2021·新高考Ⅰ卷]有一组样本数据x1，x2，…，xn，由这组数据得到新样本数据y1，y2，…，yn，其中yi＝xi＋c(i＝1，2，…，n)，c为非零常数，则( )
A．两组样本数据的样本平均数相同
B．两组样本数据的样本中位数相同
C．两组样本数据的样本标准差相同
D．两组样本数据的样本极差相同
11．[2022·河北沧州二模]某车间加工某种机器的零件数x与加工这些零件所花费的时间y之间的对应数据如下表所示：
由表中的数据可得回归直线方程 eq \(y,\s\up6(^)) ＝ eq \(b,\s\up6(^)) x＋54.9，则以下结论正确的有( )
A．相关系数r>0
B． eq \(b,\s\up6(^)) ＝0.67
C．零件数10，20，30，40，50的中位数是30
D．若加工60个零件，则加工时间一定是95.1 min
12．[2022·河北唐山二模]小李上班可以选择公交车、自行车两种交通工具，他分别记录了100次坐公交车和骑车所用时间(单位：分钟)，得到下列两个频率分布直方图：
基于以上统计信息，则( )
A．骑车时间的中位数的估计值是22分钟
B．骑车时间的众数的估计值是21分钟
C．坐公交车时间的中位数的估计值是20分钟
D．坐公交车时间的平均数的估计值小于骑车时间的平均数的估计值
三、填空题
13．[2022·山东聊城二模]如图是调查某学校高一年级男、女学生是否喜欢徒步运动而得到的等高条形图，阴影部分表示喜欢徒步的频率．已知该年级男生500人、女生400名(假设所有学生都参加了调查)，现从所有喜欢徒步的学生中按分层抽样的方法抽取23人，则抽取的男生人数为________．
14．[2022·山东潍坊三模]为了解某社区居民的2021年家庭年收入与年支出的关系，随机调查了该社区5户家庭，得到如下统计数据表：
根据上表可得回归直线方程 eq \(y,\s\up6(^)) ＝0.76x＋0.4，则t＝________．
15．[2022·河北衡水高三期末]定义一个同学数学成绩优秀的标准为“连续5次数学考试成绩均不低于120分(满分150分)”．现有甲、乙、丙三位同学连续5次数学考试成绩的数据(数据都是正整数)的描述：
①甲同学的5个数据的中位数为125，总体均值为128；
②乙同学的5个数据的中位数为127，众数为121；
③丙同学的5个数据的众数为125，极差为10，总体均值为125.
则数学成绩一定优秀的同学是________．
16．[2022·山东肥城市教学研究中心模拟预测]在对某中学高一年级学生每周体育锻炼时间的调查中，采用随机数法，抽取了男生30人，女生20人. 已知男同学每周锻炼时间的平均数为17小时，方差为11；女同学每周锻炼时间的平均数为12小时，方差为16. 依据样本数据，估计本校高一年级学生每周体育锻炼时间的方差为________．
命题点19 统计与统计案例(小题突破)
1．解析：由扇形分布图结合分层抽样知识易知样本容量为 eq \f(80,40%) ＝200，
则样本中高中生的人数为200×25%＝50，易知总体的容量为 eq \f(50,1%) ＝5 000，
结合近视率条形图得该地区高中生近视人数为5 000×50%＝2 500.
故选B.
答案：B
2．解析：由统计图可知，讲座前这10位社区居民问卷答题的正确率分别为65%，60%，70%，60%，65%，75%，90%，85%，80%，95%.对于A项，将这10个数据从小到大排列为60%，60%，65%，65%，70%，75%，80%，85%，90%，95%，因此这10个数据的中位数是第5个与第6个数的平均数，为 eq \f(70%＋75%,2) ＝72.5%＞70%，A错误．对于B项，由统计图可知，讲座后这10位社区居民问卷答题的正确率分别为90%，85%，80%，90%，85%，85%，95%，100%，85%，100%，所以讲座后这10位社区居民问卷答题的正确率的平均数为 eq \f(1,10) ×(90%＋85%＋80%＋90%＋85%＋85%＋95%＋100%＋85%＋100%)＝89.5%＞85%，B正确．对于C项，讲座后这10位社区居民问卷答题的正确率的方差s eq \\al(\s\up1(2),\s\d1(后)) ＝ eq \f(1,10) ×[(90%－89.5%)2＋(85%－89.5%)2＋…＋(85%－89.5%)2＋(100%－89.5%)2]＝ eq \f(42.25,10 000) ，所以标准差s后＝6.5%.讲座前这10位社区居民问卷答题的正确率的平均数为 eq \f(1,10) ×(60%＋60%＋65%＋65%＋70%＋75%＋80%＋85%＋90%＋95%)＝74.5%，所以讲座前这10位社区居民问卷答题的正确率的方差为s eq \\al(\s\up1(2),\s\d1(前)) ＝ eq \f(1,10) ×[(60%－74.5%)2＋(60%－74.5%)2＋…＋(90%－74.5%)2＋(95%－74.5%)2]＝ eq \f(142.25,10 000) ，所以标准差s前≈11.93%.所以s前＞s后，C错误．对于D项，讲座前问卷答题的正确率的极差为95%－60%＝35%，讲座后问卷答题的正确率的极差为100%－80%＝20%，D错误．故选B.
答案：B
3．解析：50岁以下1 000×(0.2＋0.3＋0.1)＝600人，A选项错误．
在受试者中，抗体呈阳性的人数为600×0.9＋400×0.85＝880，B选项错误．
受试者的平均年龄为25×0.2＋35×0.3＋45×0.1＋55×0.2＋65×0.1＋75×0.1＝45，C选项正确．
受试者的疫苗有效率为 eq \f(880,1 000) ×100%＝88%，D选项错误．
故选C.
答案：C
4．解析：第一组的频率为0.010×10＝0.1，前两组的频率之和为(0.010＋0.020)×10＝0.3，
知25%分位数在第二组[60，70)内，故25%分位数为60＋10× eq \f(0.25－0.1,0.2) ＝67.5.
故选C.
答案：C
5．解析：由已知得x1＋x2＋x3＝15，(x1－5)2＋(x2－5)2＋(x3－5)2＝12，
则新数据的平均数为 eq \f(1,4) (2x1＋1＋2x2＋1＋2x3＋1＋11)＝ eq \f(2（x1＋x2＋x3）＋3＋11,4) ＝11，
所以方差为 eq \f(1,4) [(2x1＋1－11)2＋(2x2＋1－11)2＋(2x3＋1－11)2＋(11－11)2]，
＝ eq \f(1,4) [4(x1－5)2＋4(x2－5)2＋4(x3－5)2]＝(x1－5)2＋(x2－5)2＋(x3－5)2＝12，
故选C.
答案：C
6．解析：由已知 eq \(x,\s\up6(－)) ＝ eq \f(1＋2＋4＋5,4) ＝3， eq \(y,\s\up6(－)) ＝ eq \f(0.5＋0.9＋2.3＋2.7,4) ＝1.6，
所以1.6＝0.58×3＋ eq \(a,\s\up6(^)) ， eq \(a,\s\up6(^)) ＝－0.14，即 eq \(y,\s\up6(^)) ＝0.58x－0.14，
x＝6时， eq \(y,\s\up6(^)) ＝0.58×6－0.14＝3.34，
故选A.
答案：A
7．解析：a＋b＝40＋20＝60，c＋d＝20＋30＝50，a＋c＝40＋20＝60，
b＋d＝20＋30＝50，ad－bc＝40×30－20×20＝800，n＝110，
χ2＝ eq \f(n（ad－bc）2,（a＋b）（c＋d）（a＋c）（b＋d）) ＝ eq \f(110×8002,60×50×60×50) ≈7.822b2，所以选项D正确，
故选BCD.
答案：BCD
13．解析：根据等高条形图可知： 喜欢徒步的男生人数为0.6×500＝300，喜欢徒步的女生人数为0.4×400＝160，
所以喜欢徒步的总人数为300＋160＝460，
按分层抽样的方法抽取23人，则抽取的男生人数为 eq \f(300,460) ×23＝15人．
答案：15
14．解析：分别求出收入和支出的平均数，
可得： eq \(x,\s\up6(－)) ＝ eq \f(8.2＋8.6＋10.0＋11.3＋11.9,5) ＝10，
eq \(y,\s\up6(－)) ＝ eq \f(6.2＋7.5＋8.0＋9.8＋t,5) ＝ eq \f(31.5＋t,5) ，
代入 eq \(y,\s\up6(^)) ＝0.76x＋0.4可得： eq \f(31.5＋t,5) ＝0.76×10＋0.4，
解得：t＝8.5.
答案：8.5
15．解析：在①中，甲同学的5个数据的中位数为125，总体均值为128，
可以找到很多反例，如118，119，125，128，150，故甲同学的数学成绩不一定优秀；
在②中，乙同学的5个数据的中位数为127，众数为121，
所以前三个数为121，121，127，则后两个数肯定大于127，故乙同学的数学成绩一定优秀；
在③中，丙同学的5个数据的众数为125，极差为10，总体均值为125，最大值与最小值的差为10，若最大值为129，则最小值为119.即119，125，125，127，129，故丙同学的数学成绩不一定优秀．
综上，数学成绩一定优秀的同学只有乙．
答案：乙
16．解析：根据平均数的计算公式，全班的平均数为 eq \(z,\s\up6(－)) ＝ eq \f(17×30＋12×20,30＋20) ＝15，
设男同学为x1，x2，…，x30，女同学为y1，y2，…，y20，
答案：19
年龄
频率
[20，30)
0.20
[30，40)
0.30
[40，50)
0.10
[50，60)
0.20
[60，70)
0.10
[70，80]
0.10
行驶里程x/万千米
1
2
4
5
维修保养费用y/万元
0.50
0.90
2.30
2.70
x
5
6.5
7
8
8.5
y
9
8
6
4
3
x/个
10
20
30
40
50
y/min
62
68
75
81
89
收入x(万元)
8.2
8.6
10.0
11.3
11.9
支出y(万元)
6.2
7.5
8.0
t
9.8