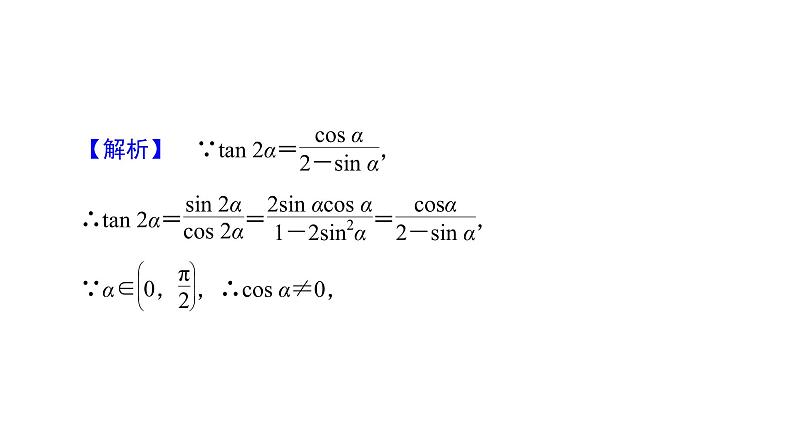
2023届高考数学二轮复习专题1第2讲三角恒等变换与解三角形课件

这是一份2023届高考数学二轮复习专题1第2讲三角恒等变换与解三角形课件，共46页。PPT课件主要包含了考情分析，真题热身，感悟高考，考点一三角恒等变换，典例1，典例2，典例3等内容，欢迎下载使用。

专题一　三角函数和解三角形
第2讲　三角恒等变换与解三角形
1．三角函数的化简与求值是高考的命题重点，其中关键是运用倍角公式、两角和与差公式进行恒等变换，“角”的变换是三角恒等变换的核心；2．正、余弦定理及应用是高考的必考内容，主要考查边、角、面积的计算及有关的范围问题，常与三角恒等变换交汇融合，解答题常处于第一题位置，注重基础知识、基本能力的考查．
自主先热身 真题定乾坤
核心拔头筹 考点巧突破
专题勇过关 能力巧提升
【解析】　设CD＝2BD＝2m>0，则在△ABD中，AB2＝BD2＋AD2－2BD·AD·cs ∠ADB＝m2＋4＋2m，在△ACD中，AC2＝CD2＋AD2－2CD·AD·cs ∠ADC＝4m2＋4－4m，
5．(2022·全国高三专题练习)△ABC中，sin2A－sin2B－sin2C＝sinB sin C.(1)求A；(2)若BC＝3，求△ABC周长的最大值．
6．(2022·全国乙卷)记△ABC内角A，B，C的对边分别为a，b，c，已知sin C sin (A－B)＝sin B sin (C－A).(1)若A＝2B，求C；(2)证明：2a2＝b2＋c2.【解析】　(1)由A＝2B，sin C sin (A－B)＝sin B sin (C－A)可得，sin C sin B＝sin B sin (C－A)，
(2)证明：由sin C sin (A－B)＝sin B sin (C－A)可得，sin C(sin A cs B－cs A sin B)＝sin B(sin Ccs A－cs C sin A)，再由正弦定理可得，ac cs B－bc cs A＝bc cs A－ab cs C，然后根据余弦定理可知，
1．高考对此部分的考查一般以“二小”或“一大”的命题形式出现．2．若无解答题，一般在选择题或填空题各有一题，主要考查三角恒等变换、解三角形，难度一般，一般出现在第4～9或第13～15题位置上．3．若以解答题命题形式出现，主要考查三角函数与解三角形的综合问题，一般出现在解答题第17题位置上，难度中等．
1．三角求值“三大类型”“给角求值”“给值求值”“给值求角”．
2．三角恒等变换“四大策略”(1)常值代换：常用到“1”的代换，1＝sin2θ＋cs2θ＝tan45°等．(2)项的拆分与角的配凑：如sin2α＋2cs2α＝(sin2α＋cs2α)＋cs2α，α＝(α－β)＋β等．(3)降次与升次：正用二倍角公式升次，逆用二倍角公式降次．(4)弦、切互化．
【易错提醒】(1)公式的使用过程要注意正确性，要特别注意公式中的符号和函数名的变换，防止出现“张冠李戴”的情况．(2)求角问题要注意角的范围，要根据已知条件将所求角的范围尽量缩小，避免产生增解．
考点二　正弦定理、余弦定理
考向1　求解三角形中的角、边(2022·安徽模拟)记△ABC的内角A，B，C的对边分别为a，b，c.已知sin C＝2sin A·sin B，点D在边AB上，且CD⊥AB.
【素养提升】(1)利用余弦定理求边，一般是已知三角形的两边及其夹角．利用正弦定理求边，必须知道两角及其中一边，且该边为其中一角的对边，要注意解的多样性与合理性．(2)三角形中的最值与范围问题主要有两种解决方法：一是利用基本不等式求得最大值或最小值；二是将所求式转化为只含有三角形某一个角的三角函数形式，结合角的范围确定所求式的范围．