2023届高考数学二轮复习专题3第3讲立体几何与空间向量课件

这是一份2023届高考数学二轮复习专题3第3讲立体几何与空间向量课件，共60页。PPT课件主要包含了专题三立体几何，考情分析，真题热身，感悟高考，典例1，典例2，典例3等内容，欢迎下载使用。

第3讲　立体几何与空间向量
空间向量是将空间几何问题坐标化的工具，是常考的重点，作为求解空间角的有力工具，通常在解答题中进行考查，属于中等难度．
自主先热身 真题定乾坤
核心拔头筹 考点巧突破
专题勇过关 能力巧提升
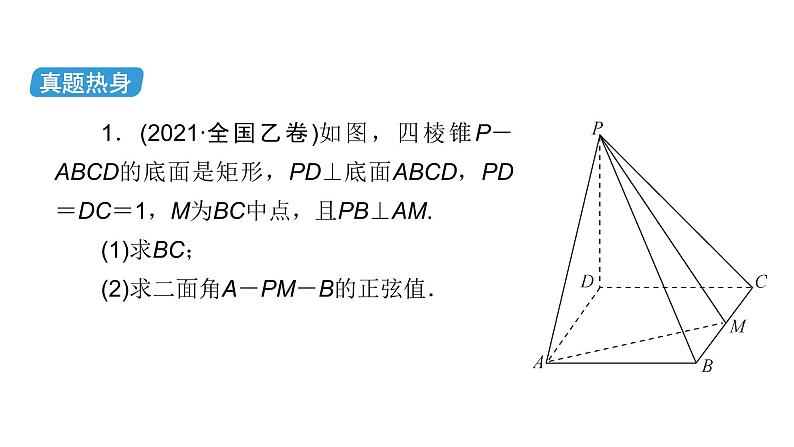
1．(2021·全国乙卷)如图，四棱锥P－ABCD的底面是矩形，PD⊥底面ABCD，PD＝DC＝1，M为BC中点，且PB⊥AM.(1)求BC；(2)求二面角A－PM－B的正弦值．
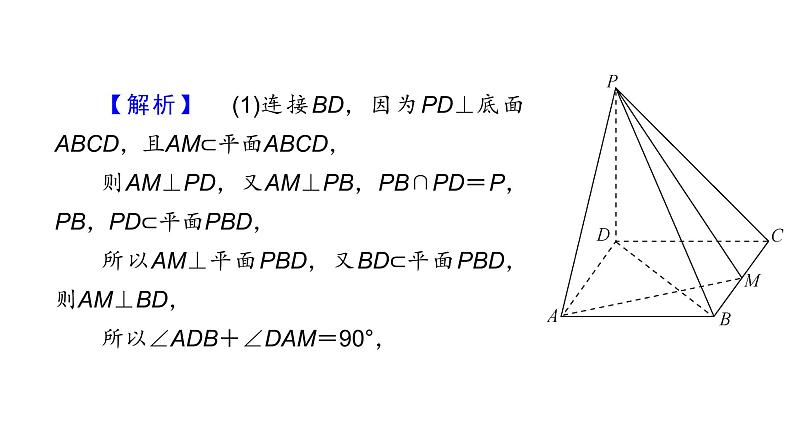
【解析】　(1)连接BD，因为PD⊥底面ABCD，且AM⊂平面ABCD，则AM⊥PD，又AM⊥PB，PB∩PD＝P，PB，PD⊂平面PBD，所以AM⊥平面PBD，又BD⊂平面PBD，则AM⊥BD，所以∠ADB＋∠DAM＝90°，
(2)因为DA，DC，DP两两垂直，故以点D为坐标原点建立空间直角坐标系如图所示，
【解析】(1)证明：在四边形ABCD中，作DE⊥AB于E，CF⊥AB于F，因为CD∥AB，AD＝CD＝CB＝1，AB＝2，所以四边形ABCD为等腰梯形，
所以AD2＋BD2＝AB2，所以AD⊥BD，因为PD⊥平面ABCD，BD⊂平面ABCD，所以PD⊥BD，又PD∩AD＝D，所以BD⊥平面PAD，又因为PA⊂平面PAD，所以BD⊥PA.
(1)求A到平面A1BC的距离；(2)设D为A1C的中点，AA1＝AB，平面A1BC⊥平面ABB1A1，求二面角A－BD－C的正弦值．
(2)取A1B的中点E，连接AE，如图，因为AA1＝AB，所以AE⊥A1B，又平面A1BC⊥平面ABB1A1，平面A1BC∩平面ABB1A1＝A1B，且AE⊂平面ABB1A1，所以AE⊥平面A1BC，在直三棱柱ABC－A1B1C1中，BB1⊥平面ABC，由BC⊂平面A1BC，BC⊂平面ABC可得AE⊥BC，BB1⊥BC，又AE，BB1⊂平面ABB1A1且相交，所以BC⊥平面ABB1A1，
所以BC，BA，BB1两两垂直，以B为原点，建立空间直角坐标系，如图，
4．(2022·全国乙卷)如图，四面体ABCD中，AD⊥CD，AD＝CD，∠ADB＝∠BDC，E为AC的中点．(1)证明：平面BED⊥平面ACD；(2)设AB＝BD＝2，∠ACB＝60°，点F在BD上，当△AFC的面积最小时，求CF与平面ABD所成的角的正弦值．
【解析】　(1)证明：因为AD＝CD，E为AC的中点，所以AC⊥DE；在△ABD和△CBD中，因为AD＝CD，∠ADB＝∠CDB，DB＝DB，所以△ABD≌△CBD，所以AB＝CB，又因为E为AC的中点，所以AC⊥BE；又因为DE，BE⊂平面BED，DE∩BE＝E，所以AC⊥平面BED，因为AC⊂平面ACD，所以平面BED⊥平面ACD.
5．(2022·浙江卷)如图，已知ABCD和CDEF都是直角梯形，AB∥DC，DC∥EF，AB＝5，DC＝3，EF＝1，∠BAD＝∠CDE＝60°，二面角F－DC－B的平面角为60°.设M，N分别为AE，BC的中点．(1)证明：FN⊥AD；(2)求直线BM与平面ADE所成角的正弦值．
【解析】　(1)过点E、D分别做直线DC、AB的垂线EG、DH并分别交于点G、H.∵四边形ABCD和EFCD都是直角梯形，AB∥DC，CD∥EF，AB＝5，DC＝3，EF＝1，∠BAD＝∠CDE＝60°，由平面几何知识易知，DG＝AH＝2，∠EFC＝∠DCF＝∠DCB＝∠ABC＝90°，则四边形EFCG和四边形DCBH是矩形，
∴DC⊥平面BCF，∠BCF是二面角F－DC－B的平面角，则∠BCF＝60°，∴△BCF是正三角形，由DC⊂平面ABCD，得平面ABCD⊥平面BCF，∵N是BC的中点，∴FN⊥BC，又DC⊥平面BCF，FN⊂平面BCF，可得FN⊥CD，而BC∩CD＝C，∴FN⊥平面ABCD，而AD⊂平面ABCD，∴FN⊥AD.
1．立体几何考查知识点突出立体、空间线线、线面关系及线面角，面面关系以及二面角展开，解答题考查空间中平行垂直问题，利用空间向量求空间角．2．解答题多出现在第18，19题的位置，考查空间中平行、垂直的证明，利用空间向量求空间角，难度中等．
设直线l，m的方向向量分别为a＝(a1，b1，c1)，b＝(a2，b2，c2).平面α，β的法向量分别为u＝(a3，b3，c3)，v＝(a4，b4，c4)(以下相同).(1)线线夹角
考点一　利用空间向量求空间角
(1)求证：PA⊥BC；(2)设点E为PC的中点，求直线AE与平面PBC所成角的正弦值．
考向2　二面角如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AD∥BC，AB＝BC＝CD＝PA＝1，AD＝2.(1)求证：平面PCD⊥平面PAC；(2)求平面PAB与平面PCD所成锐二面角的余弦值．
(2)过点B作BM⊥AD于M，以M为原点，建立空间直角坐标系，如图所示，在等腰梯形ABCD中，AD∥BC，AB＝BC＝CD＝1，AD＝2，
1．如图，四棱锥P－ABCD的底面是平行四边形，且PD⊥AB.(1)从下列两个条件中任选一个条件证明：AB⊥平面PAD.①O是AD的中点，且BO＝CO；②AC＝BD.
【解析】(1)证明：选择条件②，∵四边形ABCD为平行四边形，且AC＝BD，∴四边形ABCD为矩形，AB⊥AD.又∵AB⊥PD，且AD∩PD＝D，故AB⊥平面PAD.选择条件①，在平行四边形ABCD中，设N是BC的中点，连接ON，如图，
因为O是AD的中点，所以AB∥ON.又BO＝CO，所以ON⊥BC.所以AB⊥BC，又在平行四边形ABCD中，BC∥AD，所以AB⊥AD.又AB⊥PD，且PD∩AD＝D，AD⊂平面PAD，PD⊂平面PAD，故AB⊥平面PAD.
以O为坐标原点，ON，OD，OP所在直线分别为x轴，y轴，z轴，建立空间直角坐标系，则A(0，－2，0)，B(2，－2，0)，C(2，2，0)，P(0，0，2)，
与空间向量有关的探究性问题主要有两类：一类是探究线面的位置关系；另一类是探究线面角或二面角满足特定要求时的存在性问题．处理原则：先建立空间直角坐标系，引入参数(有些是题中已给出)，设出关键点的坐标，然后探究这样的点是否存在，或参数是否满足要求，从而作出判断．
考点二　利用空间向量解决探究性问题
如图，四棱柱ABCD－A1B1C1D1中，平面A1C1CA⊥平面ABCD，底面ABCD为菱形，AC与BD交于点O，∠ABC＝60°，AB＝AA1＝AC1＝2.(1)求证：C1O⊥平面ABCD；
【解析】(1)证明：∵AA1＝AC1，AA1＝CC1，∴AC1＝CC1，又O是AC的中点，∴C1O⊥AC，∵平面A1C1CA⊥平面ABCD，平面A1C1CA∩平面ABCD＝AC，C1O⊂平面A1C1CA，∴C1O⊥平面ABCD.
(2)∵底面ABCD是菱形，∴AC⊥BD，以O为原点，OB，OC，OC1所在直线分别为x，y，z轴建立空间直角坐标系．
【素养提升】正确分析空间几何体的特征，建立合适的空间直角坐标系，是解决此类问题的关键．
(1)求证：BE⊥平面ACB1；(2)求二面角D1－AC－B1的余弦值；(3)在棱A1B1上是否存在点F，使得直线DF∥平面ACB1？若存在，求A1F的长；若不存在，请说明理由．
【解析】(1)证明：因为A1A⊥底面ABCD，所以A1A⊥AC.又因为AB⊥AC，AA1∩AB＝A，且AA1，AB⊂平面ABB1A1，所以AC⊥平面ABB1A1，又因为BE⊂平面ABB1A1，所以AC⊥BE.
所以∠ABE＝∠AB1B.因为∠BAB1＋∠AB1B＝90°，所以∠BAB1＋∠ABE＝90°，所以BE⊥AB1.又AB1∩AC＝A，且AB1，AC⊂平面ACB1，所以BE⊥平面ACB1.