精品解析：山东省滨州市2019—2020学年下学期高一年级期末考试数学试题

这是一份精品解析：山东省滨州市2019—2020学年下学期高一年级期末考试数学试题，文件包含精品解析山东省滨州市20192020学年下学期高一年级期末考试数学试题解析版doc、精品解析山东省滨州市20192020学年下学期高一年级期末考试数学试题原卷版doc等2份试卷配套教学资源，其中试卷共29页， 欢迎下载使用。
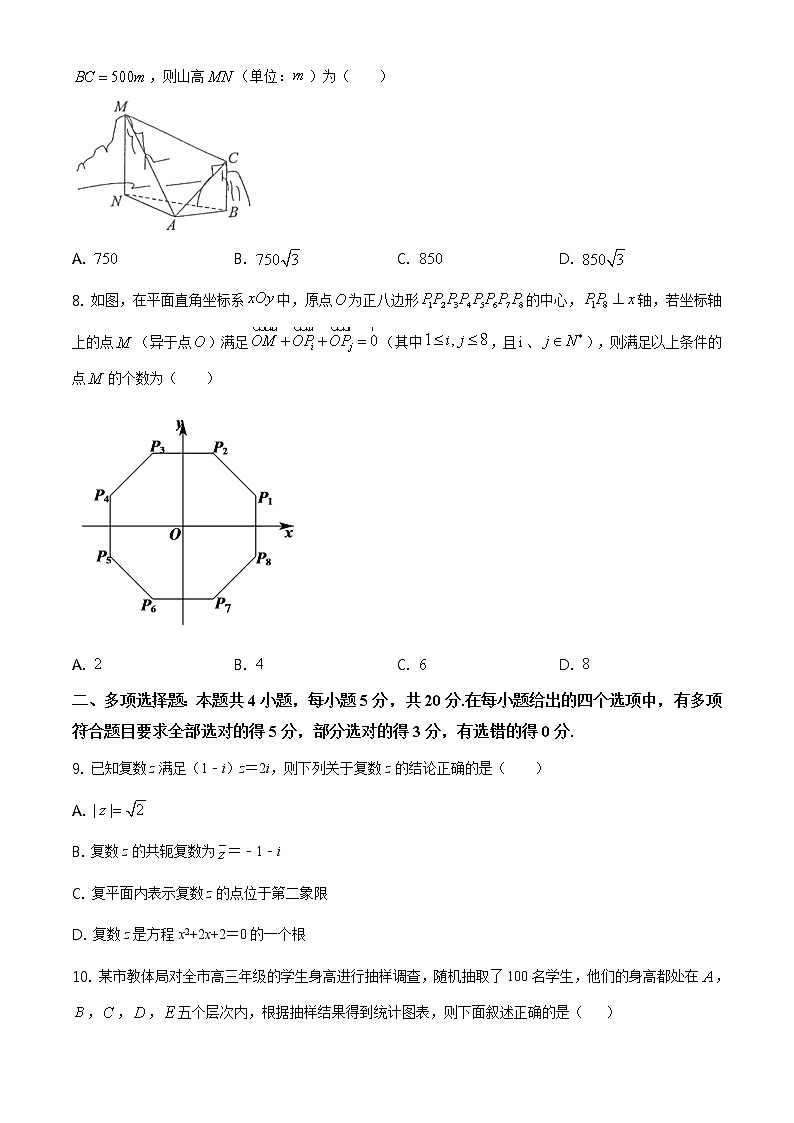
高一数学试题2020.7一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知复数是纯虚数，则实数m＝（　　）A. ﹣2 B. ﹣1 C. 0 D. 1【答案】B【解析】【分析】本题先将化简为的代数形式，再根据纯虚数的定义建立方程求参数.【详解】解：∵ 是纯虚数，∴ ，解得：，故选：B.【点睛】考查复数的代数形式以及纯虚数的定义，是基础题.2. “幸福感指数”是指某个人主观地评价他对自己目前生活状态的满意程度的指标，常用区间内的一个数来表示，该数越接近10表示满意程度越高，现随机抽取6位小区居号，他们的幸福感指数分别为5，6，7，8，9，5，则这组数据的第80百分位数是（    ）A. 7 B. 7.5 C. 8 D. 9【答案】C【解析】【分析】把该组数据从小到大排列，计算，从而找出对应的第80百分位数；【详解】该组数据从小到大排列为：5，5，6，7，8，9，且，故选：C.【点睛】本题考查一组数据的百分数问题，属于基础题.3. 设为平面，，为两条不同的直线，则下列叙述正确的是(    )A. 若，，则 B. 若，，则C. 若，，则 D. 若，，则【答案】B【解析】【分析】利用空间线线、线面、面面间的关系对每一个选项逐一分析判断得解．【详解】若，，则与相交、平行或异面，故错误；若，，则由直线与平面垂直的判定定理知，故正确；若，，则或，故错误；若，，则，或，或与相交，故错误．故选：．【点睛】本题考查命题的真假的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．4. 已知在平行四边形中，点、分别是、的中点，如果，，那么向量（　　）A.  B.  C.  D. 【答案】B【解析】【分析】作出图形，利用平面向量加法法则可求得结果.【详解】如下图所示：点、分别是、的中点，.故选：B.【点睛】本题考查平面向量的基底分解，考查计算能力，属于基础题.5. 已知圆锥的表面积为，且它的侧面展开图是一个半圆，则该圆锥的体积为（    ）A.  B.  C.  D. 【答案】A【解析】【分析】设圆锥的底面半径为，高为，母线为，根据其表面积为，得到，再由它的侧面展开图是一个半圆，得到，联立求得半径和高，利用体积公式求解.【详解】解：设圆锥的底面半径为，高为，母线为，因为其表面积为，所以，即，又因为它的侧面展开图是一个半圆，所以，即，所以，所以此圆锥的体积为.故选：A.【点睛】本题主要考查圆的面积、周长、圆锥的侧面积及体积等知识点，考查运算求解能力，属于基础题型.6. 《史记》中讲述了田忌与齐王赛马的故事，其中，田忌的上等马优于齐王的中等马，劣于齐王的上等马；田忌的中等马优于齐王的下等马，劣于齐王的中等马；田忌的下等马劣于齐王的下等马，若双方各自拥有上等马、中等马、下等马各1匹，且双方各自随机选1匹马进行1场比赛，则田忌的马获胜的概率为（    ）A.  B.  C.  D. 【答案】C【解析】【分析】本题先将所有的基本事件都列出来共9种，再将田忌的马获胜的事件选出共3种，最后计算概率即可.【详解】解：设田忌的上等马为，中等马为：，下等马为，齐王的上等马为，中等马为：，下等马为，双方各自随机选1匹马进行1场比赛产生的基本事件为：，，，，，，，，，共9种；其中田忌的马获胜的事件为：，，，共3种，所以田忌的马获胜的概率为：.故选：C.【点睛】本题考查古典概型，是基础题.7. 如图所示，为了测量山高，选择和另一座山的山顶作为测量基点，从点测得点的仰角，点的仰角，，从点测得．已知山高，则山高（单位：）为（　　）A.  B.  C.  D. 【答案】A【解析】【分析】计算出，在中，利用正弦定理求得，然后在中可计算出.【详解】在中，，为直角，则，在中，，，则，由正弦定理，可得，在中，，，.故选：A.【点睛】本题考查测量高度问题，考查正弦定理的应用，考查计算能力，属于中等题.8. 如图，在平面直角坐标系中，原点为正八边形的中心，轴，若坐标轴上的点（异于点）满足（其中，且、），则满足以上条件的点的个数为（　　）A.  B.  C.  D. 【答案】D【解析】【分析】分点在、轴进行分类讨论，可得出点、关于坐标轴对称，由此可得出点的个数.【详解】分以下两种情况讨论：①若点在轴上，则、关于轴对称，由图可知，与、与、与、与关于轴对称，此时，符合条件的点有个；②若点在轴上，则、关于轴对称，由图可知，与、与、与、与关于轴对称，此时，符合条件的点有个.综上所述，满足题中条件的点的个数为.故选：D.【点睛】本题考查符合条件的点的个数的求解，考查了平面向量加法法则的应用，属于中等题.二、多项选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求全部选对的得5分，部分选对的得3分，有选错的得0分.9. 已知复数z满足（1﹣i）z＝2i，则下列关于复数z的结论正确的是（　　）A. B. 复数z的共轭复数为＝﹣1﹣iC. 复平面内表示复数z的点位于第二象限D. 复数z是方程x2+2x+2＝0的一个根【答案】ABCD【解析】【分析】利用复数的除法运算求出，再根据复数的模长公式求出，可知正确；根据共轭复数的概念求出，可知正确；根据复数的几何意义可知正确；将代入方程成立，可知正确.【详解】因为（1﹣i）z＝2i，所以，所以，故正确；所以，故正确；由知，复数对应的点为，它在第二象限，故正确；因，所以正确.故选：ABCD.【点睛】本题考查了复数的除法运算，考查了复数的模长公式，考查了复数的几何意义，属于基础题.10. 某市教体局对全市高三年级的学生身高进行抽样调查，随机抽取了100名学生，他们的身高都处在，，，，五个层次内，根据抽样结果得到统计图表，则下面叙述正确的是（    ） A. 样本中女生人数多于男生人数 B. 样本中层人数最多C. 样本中层次男生人数为6人 D. 样本中层次男生人数多于女生人数【答案】ABC【解析】【分析】根据直方图和饼图依次判断每个选项的正误得到答案.【详解】样本中女生人数为：，男生数为，正确；样本中层人数为：；样本中层人数为：；样本中层人数为：；样本中层人数为：；样本中层人数为：；故正确；样本中层次男生人数为：，正确；样本中层次男生人数：，女生人数为，错误.故选：.【点睛】本题考查了统计图表，意在考查学生的计算能力和应用能力.11. 已知事件，，且，，则下列结论正确的是（    ）A. 如果，那么，B. 如果与互斥，那么，C. 如果与相互独立，那么，D. 如果与相互独立，那么，【答案】BD【解析】【分析】A选项在前提下，计算出，，即可判断；B选项在与互斥前提下，计算出，，即可判断；C、D选项在与相互独立前提下，计算出，， ，，即可判断.【详解】解：A选项：如果，那么，，故A选项错误；B选项：如果与互斥，那么，，故B选项正确；C选项：如果与相互独立，那么，，故C选项错误；D选项：如果与相互独立，那么，，故D选项正确.故选：BD.【点睛】本题考查在包含关系，互斥关系，相互独立的前提下的和事件与积事件的概率，是基础题.12. 如图，正方体的棱长为1，则下列四个命题正确的是（    ）A. 若点，分别是线段，的中点，则B. 点到平面的距离为C. 直线与平面所成的角等于D. 三棱柱的外接球的表面积为【答案】ACD【解析】【分析】A选项：通过平行的传递性得到结论；B选项：根据点到平面的距离为，进一步得到答案; C选项：根据直线与平面所成的角为∠，进一步得出结论；D选项：根据三棱柱的外接球的半径为正方体体对角线的一半，进一步得到答案.【详解】A选项：若点，分别是线段，的中点，则又∵所以，故A正确；B选项：连接交于点，由题易知点到平面的距离为，∵正方体的棱长为1，∴，故B错误；C选项：易知直线与平面所成的角为∠，∴∠，故C正确；D选项：易知三棱柱的外接球的半径为正方体体对角线的一半，∴∴表面积为，故D正确.故选：ACD.【点睛】本题考查命题真假的判断，通过线线平行、点到面的距离、线面角，以及外接球的知识点来考查，解题时要注意空间思维能力的培养，是中档题.三、填空题：本题共4小题，每小题5分，共20分.13. 已知，，分别为三个内角，，的对边，且，则________.【答案】【解析】【分析】根据正弦定理把已知等式中的边转化为角的正弦，利用两角和公式化简求得的值进而求得．【详解】，，，，由于为三角形内角，可得．故答案为：．【点睛】本题主要考查正弦定理的应用．解题的关键是利用正弦定理把等式中的边转化为角的正弦．14. 已知数据，，，…，的平均数为10，方差为2，则数据，，，…，的平均数为________，方差为________.【答案】    (1). 19    (2). 8【解析】【分析】由题意结合平均数公式和方差公式计算即可得解.【详解】由已知条件可得，，所以数据、、、、的平均数为，方差为故答案为：；.【点睛】本题考查了平均数与方差的计算，考查了运算求解能力，属于基础题.15. 已知，，，则与的夹角为________.【答案】【解析】【分析】本题先求，，，再根据化简整理得，最后求与的夹角为.【详解】解：∵ ，，∴ ，，，∵ ，∴ 整理得：，∴与的夹角为：.故答案为：【点睛】本题考查运用数量积的定义与运算求向量的夹角，是基础题.16. 如图，在三棱锥中，，，，且，，则二面角的余弦值是_____．【答案】【解析】【分析】取的中点，连接、，证明出，，可得出面角的平面角为，计算出、，利用余弦定理求得，由此可得出二面角的余弦值.【详解】取的中点，连接、，如下图所示：，为的中点，则，且，，，同理可得，且，所以，二面角的平面角为，由余弦定理得，因此，二面角的余弦值为.故答案为：.【点睛】本题考查二面角余弦值的计算，考查二面角的定义，考查计算能力，属于中等题.四、解答题：本题共6小题，共70分，解答应写出文字说明、证明过程或演算步骤.17. 已知向量.（1）若向量，且，求的坐标；（2）若向量与互相垂直，求实数的值.【答案】（1）或（2）【解析】【分析】（1）    因为，所以可以设求出坐标，根据模长，可以得到参数的方程.（2）    由于已知条件 可以计算出与坐标（含有参数）而两向量垂直，可以得到关于的方程，完成本题.【详解】（1）法一:设，则，所以解得所以或法二:设，因为，，所以，因为，所以解得或，所以或（2）因为向量与互相垂直所以，即而，，所以，因此，解得【点睛】考查了向量的线性表示，引入参数，只要我们能建立起引入参数的方程，则就能计算出所求参数值，从而完成本题.18. 已知、、分别为三个内角、、的对边，且，，．（1）求及的面积；（2）若为边上一点，且，______，求的正弦值．从①，②这两个条件中任选一个，补充在上面问题中，并作答．【答案】（1），；（2）选①，；选②，.【解析】【分析】（1）利用余弦定理可得出关于的二次方程，可解出的值，进而可求得的面积；（2）选①，在中，利用正弦定理可求得的值，再由可得出，进而可求得的正弦值；选②，利用正弦定理求得的值，由同角三角函数的基本关系可求得，再利用两角和的正弦公式可求得的值.【详解】（1）由余弦定理得，整理得，，解得，；（2）选①，如下图所示：在中，由正弦定理得，可得，在中，，则，所以，；选②，在中，由正弦定理得，可得，由于为锐角，则，，因此，.【点睛】本题考查利用余弦定理解三角形以及三角形面积的计算，同时也考查了三角形内角正弦值的计算，考查计算能力，属于中等题.19. 在四面体中，点，，分别是，，的中点，且，.（1）求证：平面；（2）求异面直线与所成的角.【答案】（1）证明见解析；（2）.【解析】【分析】（1）由点，分别是，的中点，得到，结合线面平行的判定定理，即可求解；（2）由（1）知和，得到即为异面直线与所成的角，在中，即可求解.【详解】（1）由题意，点，分别是，的中点，所以，因为平面，平面，所以平面；（2）由（1）知，因为点，分别是，的中点，可得，所以即为异面直线与所成的角（或其补角）.在中，，所以为等边三角形，所以，即异面直线与所成的角为.【点睛】本题主要考查了线面平行的判定与证明，以及异面直线所成角的求解，其中解答中熟记线面平行的判定定理和异面直线所成角的概念，转化为相交直线所成的角是解答的关键，着重考查推理与运算能力.20. 溺水、校园欺凌等与学生安全有关的问题越来越受到社会的关注和重视，为了普及安全教育，某市组织了一次学生安全知识竞赛，规定每队3人，每人回答一个问题，答对得1分，答错得0分．在竞赛中，甲、乙两个中学代表队狭路相逢，假设甲队每人回答问题正确的概率均为，乙队每人回答问题正确的概率分别为，且两队各人回答问题正确与否相互之间没有影响．（1）分别求甲队总得分为3分与1分的概率；（2）求甲队总得分为2分且乙队总得分为1分的概率．【答案】（1），；（2）【解析】【分析】（1）记“甲队总得分为3分”为事件，记“甲队总得分为1分”为事件，甲队得3分，即三人都回答正确，甲队得1分，即三人中只有1人回答正确，其余两人都答错，由此利用相互独立事件概率乘法公式能求出甲队总得分为3分与1分的概率．（2）记“甲队得分为2分”为事件，记“乙队得分为1分”为事件，事件即甲队三人中有2人答对，其余1人答错，事件即乙队3人中只有1人答对，其余2人答错，由题意得事件与事件相互独立，由此利用相互独立事件概率乘法公式能求出甲队总得分为2分且乙队总得分为1分的概率．【详解】解：（1）记“甲队总得分为3分”为事件，记“甲队总得分为1分”为事件，甲队得3分，即三人都回答正确，其概率为，甲队得1分，即三人中只有1人回答正确，其余两人都答错，其概率为．甲队总得分为3分与1分的概率分别为，．（2）记“甲队得分为2分”为事件，记“乙队得分为1分”为事件，事件即甲队三人中有2人答对，其余1人答错，则，事件即乙队3人中只有1人答对，其余2人答错，则，由题意得事件与事件相互独立，甲队总得分为2分且乙队总得分为1分的概率：．【点睛】本题考查概率的求法，考查相互独立事件概率乘法公式等基础知识，考查运算求解能力，属于中档题．21. 如图，在三棱锥中，底面，，，点为线段的中点，点为线段上一点.（1）求证：平面平面.（2）当平面时，求三棱锥的体积.【答案】（1）证明见解析；（2）.【解析】【分析】（1）先证明，再证明，从而证明平面，最后证明平面平面；（2）先判断点为的中点，再判断三棱锥的体积等于三棱锥的体积，最后求体积即可.【详解】（1）证明：因底面，且底面，所以.因为，且点为线段的中点，所以.又，所以平面.又平面，所以平面平面.（2）解：因为平面，平面，平面平面，所以.因为点为的中点，所以点为的中点.法一：由题意知点到平面的距离与点到平面的距离相等，所以.所以三棱锥的体积为.法二：因为平面，由题意知点到平面的距离与点到平面的距离相等.所以，又，，，，由（1）知，，又，且，所以平面，所以.所以三棱锥体积为.法三：又，，，，由（1）知：平面，且.所以.所以三棱锥的体积为.【点睛】本题考查面面垂直的证明，三棱锥的体积，是中档题.22. 2020年开始，山东推行全新的高考制度，新高考不再分文理科，采用“3+3”模式，其中语文、数学、外语三科为必考科目，满分各150分，另外考生还需要依据想考取的高校及专业要求，结合自己的兴趣爱好等因素，在思想政治、历史、地理、物理、化学、生物6门科目中自选3门参加考试（6选3），每科满分100分，2020年初受疫情影响，全国各地推迟开学，开展线上教学．为了了解高一学生的选科意向，某学校对学生所选科目进行线上检测，下面是100名学生的物理、化学、生物三科总分成绩，以组距20分成7组：[160，180），[180，200），[200，220），[220，240），[240，260），[260，280），[280，300]，画出频率分布直方图如图所示．（1）求频率分布直方图中a的值；（2）由频率分布直方图；（i）求物理、化学、生物三科总分成绩的中位数；（ii）估计这100名学生的物理、化学、生物三科总分成绩的平均数（同一组中的数据用该组区间的中点值作代表）；（3）为了进一步了解选科情况，由频率分布直方图，在物理、化学、生物三科总分成绩在[220，240）和[260，280）的两组中，用分层随机抽样的方法抽取7名学生，再从这7名学生中随机抽取2名学生进行问卷调查，求抽取的这2名学生来自不同组的概率．【答案】（1）；（2）（i）（ii）（3）.【解析】【分析】（1）根据7组频率和为1列方程可解得结果；（2）（i）根据前三组频率和为，前四组频率和为可知中位数在第四组，设中位数为，根据即可解得结果；（ii）利用各组的频率乘以各组的中点值，再相加即可得解；（3）根据分层抽样可得从成绩在[220，240）的组中应抽取人，从成绩在[260，280）的组中应抽取人，再用列举法以及古典概型的概率公式可得解.【详解】（1）由，得；（2）（i）因为，，所以中位数在，设中位数为，所以，解得，所以物理、化学、生物三科总分成绩的中位数为；（ii）这100名学生的物理、化学、生物三科总分成绩的平均数为（3）物理、化学、生物三科总分成绩在[220，240）和[260，280）的两组中的人数分别为：人，人，根据分层随机抽样可知，从成绩在[220，240）的组中应抽取人，记为，从成绩在[260，280）的组中应抽取人，记为，从这7名学生中随机抽取2名学生的所有基本事件为：，，共有种，其中这2名学生来自不同组的共有种，根据古典概型的概率公式可得所求概率为.【点睛】本题考查了利用直方图求中位数、平均数，考查了利用直方图求参数，考查了分层抽样，考查了古典概型的概率公式，属于中档题.