期末测试卷03-2020-2021学年高一

这是一份期末测试卷03-2020-2021学年高一，文件包含期末测试卷03A4考试版docx、期末测试卷03参考答案docx等2份试卷配套教学资源，其中试卷共11页， 欢迎下载使用。
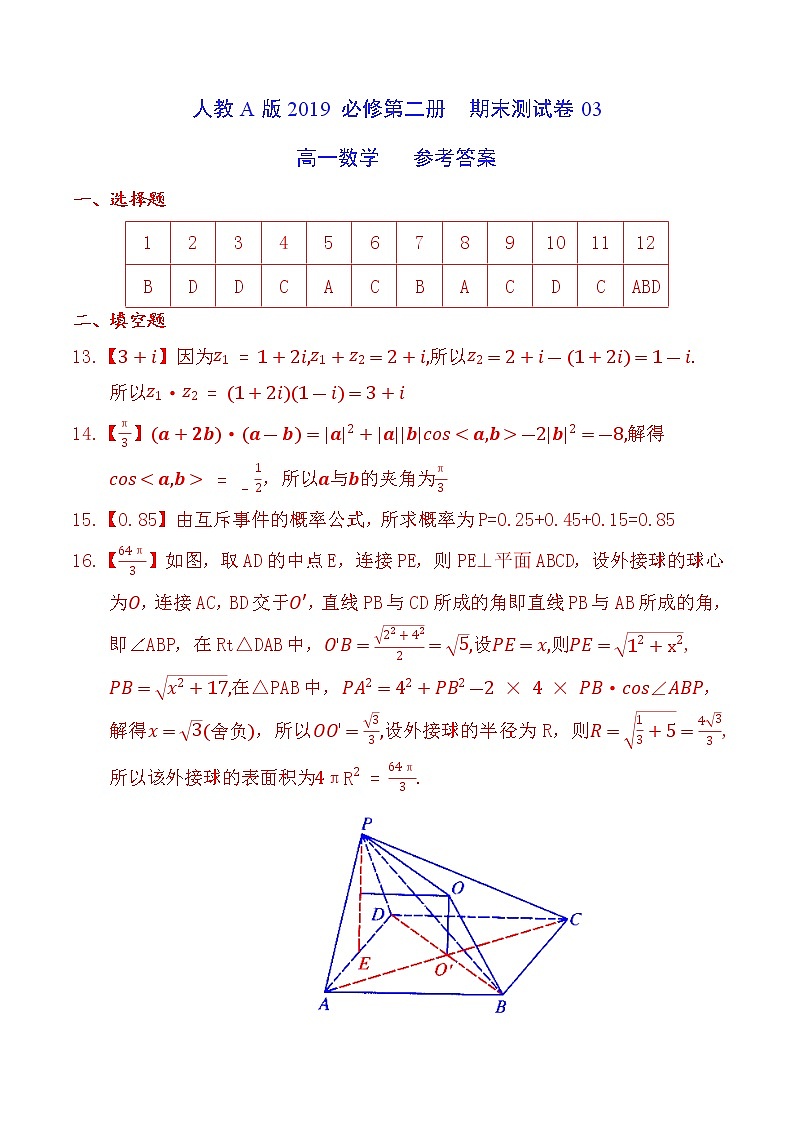
人教A版2019 必修第二册  期末测试卷03高一数学   参考答案一、选择题123456789101112BDDCACBACDCABD二、填空题13.【】因为所以    所以14.【】解得    ，所以与的夹角为15.【0.85】由互斥事件的概率公式，所求概率为P=0.25+0.45+0.15=0.8516.【】如图，取AD的中点E，连接PE，则PE⊥平面ABCD，设外接球的球心为，连接AC，BD交于，直线PB与CD所成的角即直线PB与AB所成的角，即∠ABP，在Rt△DAB中，设则,    在△PAB中，，解得，所以设外接球的半径为R，则,所以该外接球的表面积为    17.(1)因为，所以，      又因为·,所以所以      即向量,的夹角为   (2)18.(1)因为所以，      所以,      即      所以,因为，∴所以(2)由余弦定理得,因为，   所以,化简得，所以,又因为，所以△ABC为等边三角形.19.(1)设DM与FG交于点P，连接PE.      在△BCD中，易知FG//BC，∴      ∵，∴,∴，∴在△AMD中，      PE//AM，又∵PE平面EFG，AM平面EFG，      ∴AM//平面EFG.(2)∵AB=AC，DB=DC，M为BC中点，∴AM⊥BC，DM⊥BC，又∵AM∩DM=M，所以   BC⊥平面ADM.∵FG//BC，∴FG⊥平面ADM，又∵FG平面EFG，所以平面ADM⊥平面EFG， 得证. 20.(1)截面AEGF如图所示，其中点G为棱CC1上靠近点C1的四等分点.        (2)连接A1C1，设其与B1D1的交点为，连接，      由题意可知AB⊥平面BCC1B1，∵BC平面BCC1B1，BC1平面BCC1B1，∴AB⊥BC，AB⊥BC1，∴∠C1BC即为二面角C1-AB-C的平面角，∴∠C1BC=60°，      所以∵四边形A1B1C1D1为正方形，∴A1C1⊥B1D1，又∵A1C1⊥B1B，      B1B∩B1D1=B1，∴A1C1⊥平面BB1D1D，∴直线为直线在平面BB1D1D上      的投影，∴∠即为直线A1B和平面BB1D1D所成的角.在Rt△中，      ∴即直线直线A1B和平面BB1D1D所成的角的余弦值为   (3)∵BE=BB1，∴      由(2)知⊥平面，又∵，∴21.(1)分别求出每组的频率，画出的频率分布直方图如图所示：        设女、男柜员员工的月平均不满意次数分别为，则        因为，所以女员工的满意度比男员工的高.(2)在抽取的员工中，女员工不满意次数不少于20的员工人数为2人，男员工为3人，运用枚举法易知，任意抽取3人的情况有10种，男柜员不少于女柜员的情况有7种，所以所求概率为.22.(1)在Rt△GPC中，PG=2，∠PCA=30°，所以CP=      BP=∴BC=BP+CP=6+4=10m(2)连接GH，AP，∵∠GPH=180°-120°=60°，  在△GPH中，由余弦定理得    所以GH=，由正弦定理得  ,即点A到点P的距离为(3)   因为,   所以，   即所以，   当且仅当，即时等号成立，所以当时，三角形ABC区域面积最小，最小值是