专题25 一元函数的导数及其应用（单元测试卷）-2020-2021学年高中数学新教材人教A版选择性必修配套提升训练

专题25 《一元函数的导数及其应用》单元测试卷

一、单选题

1．（2020·夏津第一中学高二期中）设函数，则（    ）

A．0 B．1 C．2 D．－1

【答案】B

【解析】

因为，

所以.

故选：B.

2．（2019·辰溪县第一中学高二月考）已知函数，求(    )

A． B．5 C．4 D．3

【答案】B

【解析】

由题意，函数，则，

所以.

故答案为：B.

3．（2020·黑山县黑山中学高二月考）已知函数，且，则曲线在处的切线方程为（    ）

A． B．

C． D．

【答案】B

【解析】

，，解得，即，，则，，曲线在点处的切线方程为，即.

4．（2020·湖北省高二期中）若函数不是单调函数，则实数的取值范围是（    ）

A． B． C． D．

【答案】D

【解析】

的定义域为，，

令解得.

由于函数在上不是单调函数，

所以，解得.

故选：D

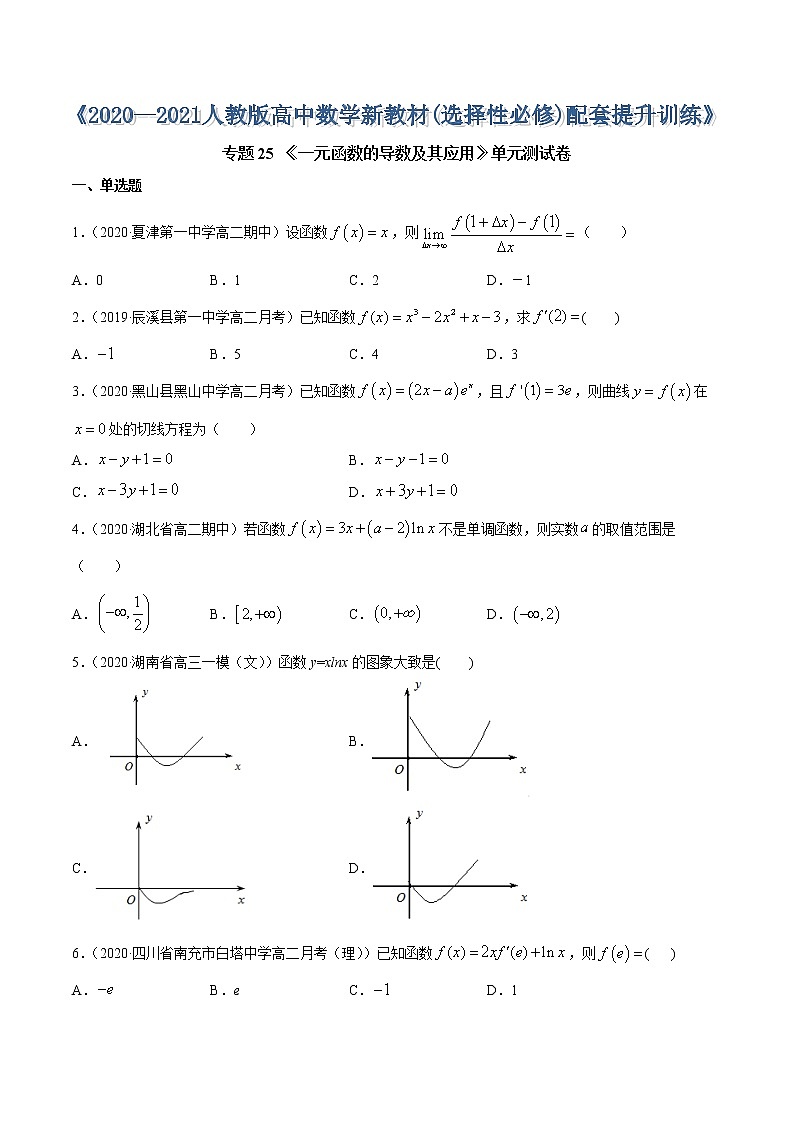
5．（2020·湖南省高三一模（文））函数y=xlnx的图象大致是(    )

A．   B．

C． D．

【答案】D

【解析】

因为y=xlnx，故可得

令，可得；令，可得，

故函数在区间上单调递减，在区间单调递增，

又因为当时，，故排除；

又时，，故函数在区间上有一个零点，故排除C.

故选：D.

6．（2020·四川省南充市白塔中学高二月考（理））已知函数，则(   )

A． B．e C． D．1

【答案】C

【解析】

由题得，

所以.

故选：C.

7．（2020·夏津第一中学高二期中）函数有（    ）

A．极大值6，极小值2 B．极大值2，极小值6

C．极小值－1，极大值2 D．极小值2，极大值8

【答案】A

【解析】

令，解得，则随的变化如下表

所以，当时，函数有极大值为；当时，函数有极小值为.

故选:A.

8．（2020·福建省高三其他（文））若函数的最大值为，则实数的取值范围为（    ）

A． B． C． D．

【答案】C

【解析】

当时，，，

若，则在恒成立，在，

且时，，函数的最大值不可能为，

，

当时，得，当时，，

在单调递增，在单调递减，

，

当时，，

，

故选：C.

二、多选题

9．（2019·福建省莆田一中高二期末）（多选题）下列函数中，既是奇函数又在区间上单调递增的是（    ）

A． B． C． D．

【答案】ABD

【解析】

由奇函数定义可知，A、B、D均为奇函数，C为偶函数，所以排除C；

对于选项A，，所以在上单调递增；

对于选项B，，所以在上单调递增；

对于选项D，，所以在上单调递增.

故选：ABD

10．（2020·江苏省高二期中）直线能作为下列（    ）函数的图像的切线.

A． B． C． D．

【答案】BCD

【解析】

，故，无解，故排除；

，故，故，即曲线在点的切线为，正确；

，故，取，故曲线在点的切线为，正确；

，故，故，曲线在点的切线为，正确；

故选：.

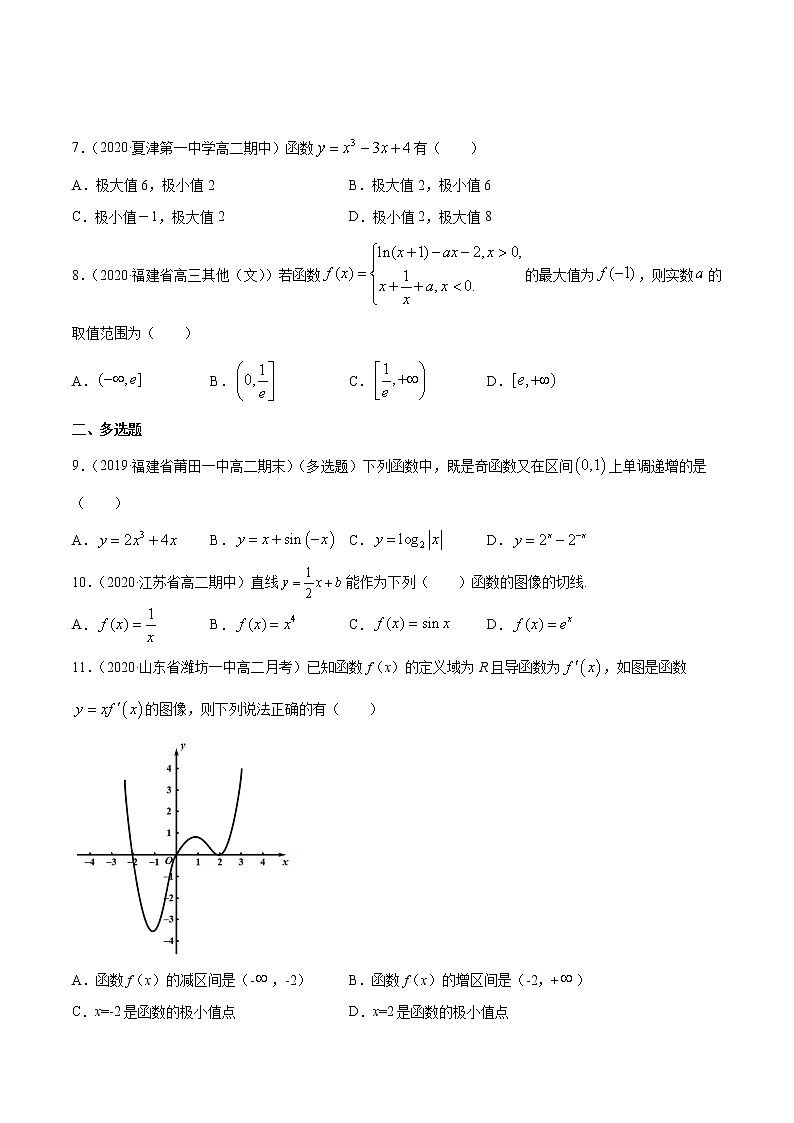
11．（2020·山东省潍坊一中高二月考）已知函数f（x）的定义域为R且导函数为，如图是函数的图像，则下列说法正确的有（    ）

A．函数f（x）的减区间是（-，-2） B．函数f（x）的增区间是（-2，+）

C．x=-2是函数的极小值点 D．x=2是函数的极小值点

【答案】ABC

【解析】

当时，，故，函数单调递增；

当时，，故，函数单调递增；

当时，，故；

当时，，故，函数单调递减；

对比选项知：故正确.

故选：.

12．（2020·南京市江宁高级中学高二期中）已知函数的导函数的图象如图所示，则下列判断正确的是（    ）

A．函数在区间内单调递增

B．当时，函数取得极小值

C．函数在区间内单调递增

D．当时，函数有极小值

【答案】BC

【解析】

对于A，函数在区间内有增有减，故A不正确；

对于B，当时，函数取得极小值，故B正确；

对于C，当时，恒有，则函数在区间上单调递增，故C正确；

对于D，当时，，故D不正确.

故选：BC

三、填空题

13．（2020·夏津第一中学高二期中）曲线y＝x2+lnx在点（1，1）处的切线方程为_____．

【答案】

【解析】

，在点（1，1）处的切线斜率为，所以切线方程为.

14．（2020·四川省北大附中成都为明学校高二月考（理））函数的单调递增区间为_______.

【答案】

【解析】

函数有意义，则： ，且： ，由 结合函数的定义域可得函数的单调递增区间为，故答案为.

15.（2020·四川省北大附中成都为明学校高二月考（理））若函数在处取得极小值，则__________．

【答案】

【解析】

求导函数可得，所以，解得 或，

当时，，函数在处取得极小值，符合题意；

当时，，函数在处取得极大值，不符合题意，不符合题意，所以.

16．（2020·浙江省宁波诺丁汉附中高二期中）已知函数则的最小值为________，最大值为_______.

【答案】       

【解析】

则当时，，当时，，

所以在上单调递减，在上单调递增，则当时，；

又，所以.

故答案为：   ；.

四、解答题

17．（2018·营口市第二高级中学高二月考（文））设，（），曲线在点处的切线垂直于轴.

（1）求的值；

（2）求函数的单调区间.

【答案】（1）；（2）的单调递增区间为，单调递减区间为.

【解析】

（1）由于，依题意，解得.

（2）由（1）知，所以在上递增，在上递增.

也即的单调递增区间为，单调递减区间为.

18．（2020·福建省高二月考）已知函数在处有极值.

（1）求的值；

（2）求函数在上的最大值与最小值.

【答案】（1），；（2）最大值为，最小值为

【解析】

（1）由题可知，，的定义域为，

，

由于在处有极值，

则，即，

解得：，，

（2）由（1）可知，其定义域是，

，

令，而，解得，

由，得；由，得，

则在区间上，，，的变化情况表如下：

可得，

，，

由于，则，

所以，

函数在区间上的最大值为，最小值为.

19．（2020·江西省新余一中高二月考（理））某同学大学毕业后，决定利用所学专业进行自主创业，经过市场调查，生产一小型电子产品需投入固定成本2万元，每生产万件，需另投入流动成本万元，当年产量小于万件时，（万元）；当年产量不小于7万件时，（万元）.已知每件产品售价为6元，假若该同学生产的商品当年能全部售完.

（1）写出年利润（万年）关于年产量（万件）的函数解析式；（注：年利润=年销售收入-固定成本-流动成本）

（2）当年产量约为多少万件时，该同学的这一产品所获年利润最大？最大年利润是多少？

（取）.

【答案】（1）  （2）当年产量约为万件，该同学的这一产品所获年利润最大，最大利润为万元

【解析】

（1）产品售价为元，则万件产品销售收入为万元.

依题意得，当时，，

当时，，

；

（2）当时，，

当时，的最大值为（万元），

当时，，

当时，单调递增，当单调递减，

当时，取最大值（万元），

当时，取得最大值万元，

即当年产量约为万件，该同学的这一产品所获年利润最大，最大利润为万元.

20．（2020·横峰中学高二开学考试（理））已知曲线的方程是．

（1）求曲线在处的切线方程；

（2）若，且直线与曲线相切于点，求直线的方程及切点坐标．

【答案】（1）；（2）直线的方程为，切点坐标为．

【解析】

（1）∵，

∴，

∴，

∴的斜率为，且过点，

∴直线的方程为，即；

（2）直线过原点，则，由点在曲线上，

得，

∴，

又，所以，

又，

∴，整理得，

∵，∴，此时，，

∴直线的方程为，切点坐标为．

21．（2020·天津大钟庄高中高二月考）已知函数 (mR)

（1）当时，

①求函数在x=1处的切线方程；

②求函数在上的最大，最小值．

（2）若函数在上单调递增，求实数的取值范围；

【答案】（1）①；②函数在上的最大值为，最小值为；（2）.

【解析】

（1）当时，.

①当x=1时，，

所以函数在x=1处的切线的斜率为，因此切线方程为：

；

②因为，所以当时，，函数单调递减，

当时，，函数单调递增，

所以当时，函数有极小值，

而，

所以函数在上的最大值为，最小值为；

（2），

因为函数在上单调递增，

所以 在时恒成立，

即在时恒成立，设，，

因为当时，函数单调递增，所以，

因此要想在时恒成立，只需.

所以当函数在上单调递增时，实数的取值范围为.

22．（2020·黄冈中学第五师分校高二期中（理））已知函数．

（1）若函数有两个零点，求的取值范围；

（2）证明：当时，关于的不等式在上恒成立．

【答案】（1）；（2）

【解析】

（1）令，；

令，，

令，解得，令，解得，

则函数在上单点递增，在上单点递减，．

要使函数有两个零点，则函数的图像与有两个不同的交点．

则，即实数的取值范围为．    

（2），；

设，；

设，，则在上单调递增.

又，.，使得，即，.

当时，；当时，；

在上单调递增，在上单调递减.

.

设，.

当时，恒成立，则在上单调递增，

，即当时，.  

•    当时，关于的不等式在上恒成立.
•