济南市章丘区第四中学2022届九年级12月月考数学试卷(含答案)

这是一份济南市章丘区第四中学2022届九年级12月月考数学试卷(含答案)，共15页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
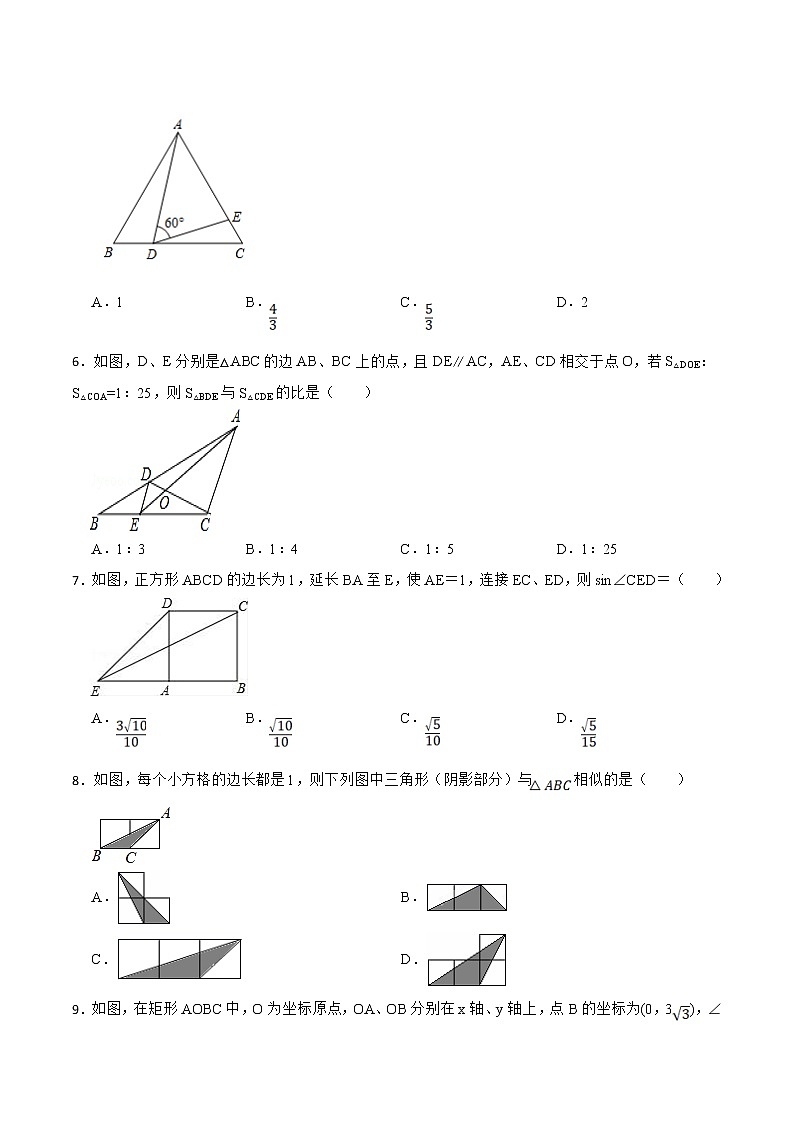
 山东省济南市章丘区第四中学2021-2022学年九年级上学期12月月考数学试题一、单选题1．在Rt△ABC中，∠C=90°，AC=12，BC=5，则sinA的值为（　　）   A． B． C． D．2．由五个相同的立方体搭成的几何体如图所示，则它的左视图是(　　)A． B．C． D．3．抛物线 的顶点坐标是（　　）A．（﹣1，2） B．（﹣1，﹣2）C．（1，﹣2） D．（1，2）4．已知：点，，都在反比例函数图象上（），则、、的关系是（　　）A． B． C． D．5．如图，ABC是等边三角形，点D、E分别在BC、AC上，且∠ADE＝60°，AB＝9，BD＝3，则CE的长等于（　　）A．1 B． C． D．26．如图，D、E分别是△ABC的边AB、BC上的点，且DE∥AC，AE、CD相交于点O，若S△DOE：S△COA=1：25，则S△BDE与S△CDE的比是（　　）A．1：3 B．1：4 C．1：5 D．1：257．如图，正方形ABCD的边长为1，延长BA至E，使AE＝1，连接EC、ED，则sin∠CED＝（　　）A． B． C． D．8．如图，每个小方格的边长都是1，则下列图中三角形（阴影部分）与相似的是（　　）A． B．C． D．9．如图，在矩形AOBC中，O为坐标原点，OA、OB分别在x轴、y轴上，点B的坐标为(0，3)，∠ABO＝30°，将△ABC沿AB所在直线对折后，点C落在点D处，则点D的坐标为(　　)A．(，) B．(2，)C．(，) D．(，3﹣)10．在二次函数y=x2-2x-3中，当时，y的最大值和最小值分别是（　　）A．0，4 B．0，3 C．3，4 D．0，011．将抛物线y=﹣5x2+1向左平移1个单位长度，再向下平移2个单位长度，所得到的抛物线为（　　）A．y=﹣5（x+1）2﹣1 B．y=﹣5（x﹣1）2﹣1C．y=﹣5（x+1）2+3 D．y=﹣5（x﹣1）2+312．已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（　　）  A．1或﹣5 B．﹣1或5 C．1或﹣3 D．1或3二、填空题13．在中，，，则　     　．14．如图，直线，，，，则的长是　     　．15．如图，过y轴上任意一点p，作x轴的平行线，分别与反比例函数和的图象交于A点和B点．若C为x轴上任意一点，连接，则的面积为　     　．16．如图，已知点P（6，3），过点P作PM⊥x轴于点M，PN⊥y轴于点N，反比例函数的图象交PM于点A，交PN于点B．若四边形OAPB的面积为12，则k=　     　．17．如图，已知二次函数 y=ax2+bx+c 的图象与 x 轴交于 A（1，0），B（3，0）两点，与 y 轴交于点 C（0，3），则二次函数的图象的顶点坐标是　          　．18．二次函数y=x2-2x-3的图象如图所示，若线段AB在x轴上，且AB为2个单位长度，以AB为边作等边△ABC，使点C落在该函数y轴右侧的图象上，则点C的坐标为　                    　三、解答题19．（1）计算：（2）已知是锐角，且，计算：．20．用适当的方法解下列方程．    （1）3x（x+3）＝2（x+3）（2）2x2﹣4x﹣3＝0．21．如图，将矩形ABCD沿CE向上折叠，使点B落在AD边上的点F处，AB=8，BC=10．（1）求证：△AEF∽△DFC；（2）求线段EF的长度．22．如图，一艘轮船位于灯塔P的北偏东60°方向，与灯塔P的距离为80海里的A处，它沿正南方向航行一段时间后，到达位于灯塔P的南偏东45°方向的B处，求此时轮船所在的B处与灯塔P的距离．（参考数据：≈2.449，结果保留整数）23．如图，在平面直角坐标系中，已知OA=12厘米，OB=6厘米．点P从点O开始沿OA边向点A以1厘米/秒的速度移动；点Q从点B开始沿BO边向点O以1厘米/秒的速度移动．如果P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6），那么，当t为何值时，△POQ与△AOB相似？ 24．水果店张阿姨以每斤2元的价格购进某种水果若干斤，然后以每斤4元的价格出售，每天可售出100斤，通过调查发现，这种水果每斤的售价每降低0.1元，每天可多售出20斤，为保证每天至少售出260斤，张阿姨决定降价销售．（1）若将这种水果每斤的售价降低x元，则每天的销售量是　　         　斤。（用含x的代数式表示）（2）销售这种水果要想每天盈利300元，张阿姨需将每斤的售价降低多少元？25．如图，反比例函数的图象与一次函数的图象交于，两点．（1）求反比例函数与一次函数的解析式；（2）根据图象回答：当x取何值时，反比例函数的值大于一次函数的值．（3）求的面积．26．如图，在平面直角坐标系中，已知的两直角边、分别在x轴的负半轴和y轴的正半轴上，且、的长满足，的平分线交x轴于点C，过点C作的垂线，垂足为点D，交y轴于点E.（1）求线段的长.（2）求直线所对应的函数关系式.（3）若M是射线上的一个动点，在坐标平面内是否存在点P，使以A、B、M、P为顶点的四边形是矩形？若存在，请求出点P的坐标；若不存在，请说明理由.27．如图，已知二次函数y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣1，图象经过B（﹣3，0）、C（0，3）两点，且与x轴交于点A．（1）求二次函数y＝ax2+bx+c（a≠0）的表达式；（2）在抛物线的对称轴上找一点M，使△ACM周长最短，求出点M的坐标；（3）若点P为抛物线对称轴上的一个动点，直接写出使△BPC为直角三角形时点P的坐标．
答案1-12 DDDCD  BBCAA  AB13．【答案】30°14．【答案】615．【答案】316．【答案】617．【答案】（2，-1）18．【答案】(1+，3)或(2，-3)19．【答案】（1）解：原式（2）解：则20．【答案】（1）解：3x(x＋3)＝2(x＋3)3x(x＋3) -2(x＋3) ＝0(x＋3) (3x-2) ＝03x-2＝0或 x＋3＝0∴x1＝，x2＝－3；（2）解：2x2－4x－3＝0a=2，b=-4，c=-3，△=16+24=40＞0，，∴x1＝1＋，x2＝1－.21．【答案】（1）证明：∵四边形ABCD是矩形， ∴∠A=∠D=∠B=90°，CD=AB=8，根据折叠的性质得∠EFC=∠B=90°，∴∠AFE+∠AEF=∠AFE+∠DFC=90°，∴∠AEF=∠DFC，∴△AEF∽△DFC；（2）解：根据折叠的性质得：CF=BC=10，BE=EF， ∴ ，∴AF=4，∵AE=AB-BE=8-EF，∴EF2=AE2+AF2，即EF2=（8-EF）2+42，解得： ．22．【答案】解：作PC⊥AB于C点，∴∠APC=30°，∠BPC=45° ，AP=80（海里），在Rt△APC中，cos∠APC=，∴PC=PA•cos∠APC=40（海里），在Rt△PCB中，cos∠BPC=，∴PB==40≈98（海里），答：此时轮船所在的B处与灯塔P的距离是98海里．23．【答案】解：①若△POQ∽△AOB时，，即，整理得：12﹣2t=t，解得：t=4．②若△POQ∽△BOA时，，即，整理得：6﹣t=2t，解得：t=2．∵0≤t≤6，∴t=4和t=2均符合题意，∴当t=4或t=2时，△POQ与△AOB相似．24．【答案】（1）100+200x（2）解：根据题意得：（4﹣2﹣x）（100+200x）=300，解得：x= ​或x=1，∵ 每天至少售出260斤，∴ x=1  答：张阿姨需将每斤的售价降低1元．25．【答案】（1）解：∵A（1，3）在的图象上，∴k=3，∴又∵B（n，﹣1）在的图象上，∴n=﹣3，即B（﹣3，﹣1）∴解得：m=1，b=2，∴反比例函数的解析式为，一次函数的解析式为y=x+2．（2）解：从图象上可知，当x＜﹣3或0＜x＜1时，反比例函数的值大于一次函数的值．（3）解：设一次函数与x轴交点为C，令一次函数值y=0，得x=-2，∴C（-2，0）∴S△ABO=S△BOC+S△AOC=×|OC|×|yB|+×|OC|×|yA|=×2×1+×2×3=4.26．【答案】（1）解：∵，∴，，在直角中，；（2）解：在和中，平分，于点O，于点D，∴，设，则，.在和中，∵，，∴，∴，即，解得：.即，，则C的坐标是.设AB的解析式是y=kx+b，根据题意得解得：则直线AB的解析式是设所对应的解析式是，则4+m=0，则m=-4．则直线所对应的解析式是.（3）解：①当AB为矩形的边时，如图所示矩形AM1P1B，易知BC的直线方程为y=2x+6，设M1（m，2m+6），P1（x，y），因为A（-8，0），B（0，6），则AM12=（m+8）2+（2m+6）2，=5m2+40m+100，BM12=m2+（2m+6-6）2=5m2，AB=10，根据AB2+AM12=BM12得100+5m2+40m+100=5m2，m=-5，∴M1（-5，-4），BM1中点坐标为，BM1中点同时也是AP1中点，则有，解得P1（3，2）②当AB为矩形的对角线时，此时有AB2=AM22+BM22，即100=5m2+40m+100+5m2，m=-4或m=0（舍去），∴M2（-4，-2），AB中点坐标为（-4，3），AB中点同时也是P2M2中点，则有，解得P2（-4，8）综上可得，满足条件的P点的坐标为P1（3，2）或P2（-4，8）．27．【答案】（1）解：∵二次函数y＝ax2+bx+c（a≠0）的对称轴为直线x＝﹣1，点B的坐标为（﹣3，0），∴点A的坐标为（1，0）．将A（1，0），B（﹣3，0），C（0，3）代入y＝ax2+bx+c，得：，解得：，∴二次函数的表达式为y＝﹣x2﹣2x+3．（2）解：连接BC，交直线x＝﹣1于点M，如图1所示．∵点A，B关于直线x＝﹣1对称，∴AM＝BM．∵点B，C，M三点共线，∴此时AM+CM取最小值，最小值为BC．设直线BC的函数表达式为y＝kx+d（k≠0），将B（﹣3，0），C（0，3）代入y＝kx+d，得：，解得：，∴直线BC的函数表达式为y＝x+3．当x＝﹣1时，y＝x+3＝2，∴当点M的坐标为（﹣1，2）时，△ACM周长最短．（3）使△BPC为直角三角形时点P的坐标为（﹣1，﹣2），（﹣1，），（﹣1，）或（﹣1，4）【解答】解：（3）设点P的坐标为（﹣1，m），∵点B的坐标为（﹣3，0），点C的坐标为（0，3），∴PB2＝[﹣3﹣（﹣1）]2+（0﹣m）2＝m2+4，PC2＝[0﹣（﹣1）]2+（3﹣m）2＝m2﹣6m+10，BC2＝[0﹣（﹣3）]2+（3﹣0）2＝18．分三种情况考虑（如图2）：①当∠BCP＝90°时，BC2+PC2＝PB2，∴18+m2﹣6m+10＝m2+4，解得：m＝4，∴点P的坐标为（﹣1，4）；②当∠CBP＝90°时，BC2+PB2＝PC2，∴18+m2+4＝m2﹣6m+10，解得：m＝﹣2，∴点P的坐标为（﹣1，﹣2）；③当∠BPC＝90°时，PB2+PC2＝BC2，∴m2+4+m2﹣6m+10＝18，整理得：m2﹣3m﹣2＝0，解得：m1＝，m2＝，∴点P的坐标为（﹣1，）或（﹣1，）．综上所述：使△BPC为直角三角形时点P的坐标为（﹣1，﹣2），（﹣1，），（﹣1，）或（﹣1，4）．