北师大版九年级下册4 圆周角和圆心角的关系第1课时达标测试

这是一份北师大版九年级下册4 圆周角和圆心角的关系第1课时达标测试，共5页。试卷主要包含了圆周角，圆周角定理，圆周角定理的推论等内容，欢迎下载使用。
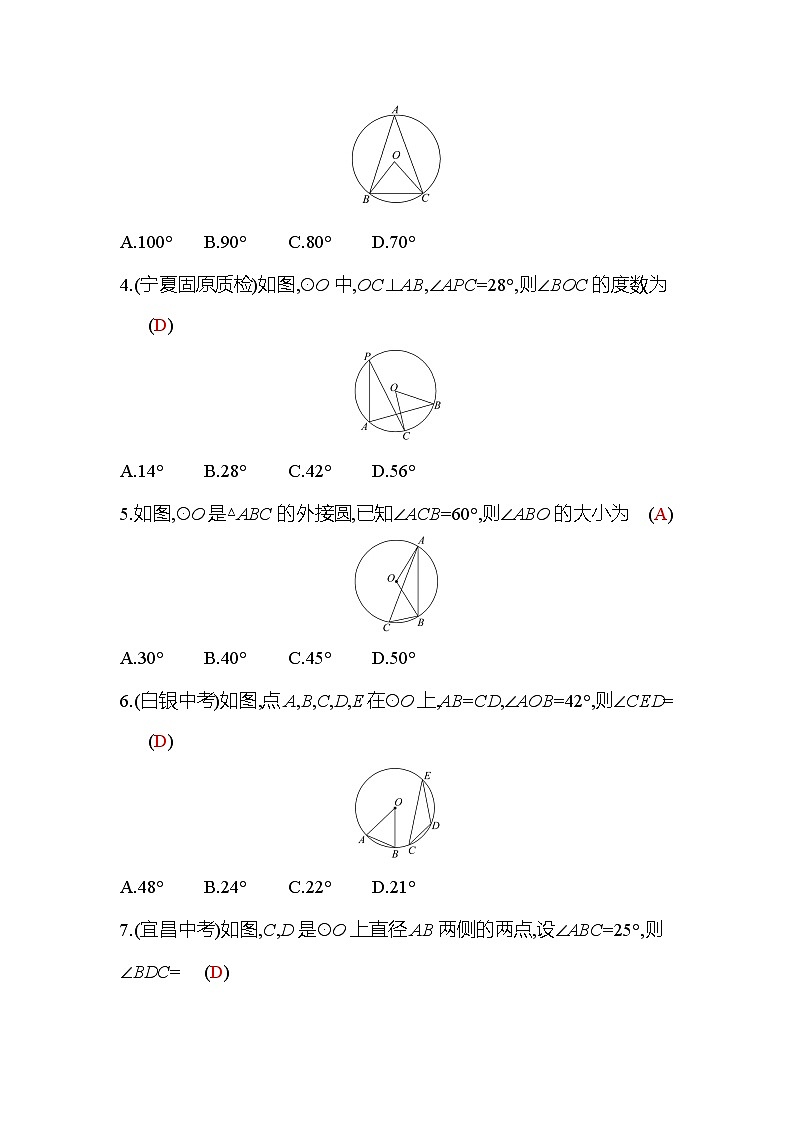
4　圆周角和圆心角的关系第1课时1.圆周角:角的顶点在　圆　上,并且两边都与圆相交的角叫做圆周角. 2.圆周角定理:圆周角的度数等于它所对弧上的　圆心角　度数的一半. 3.圆周角定理的推论:同弧或等弧所对的圆周角　相等　. 根据圆周角定义,识别它与圆心角的区别;利用圆周角定理及推论,确定它们的数量关系,进行计算.1.(西宁模拟)下列四个图中,∠x是圆周角的是 (C)2.(乌鲁木齐模拟)如图,∠1、∠2、∠3、∠4的大小关系是 (B)A.∠4<∠1<∠2<∠3  B.∠4<∠1=∠3<∠2C.∠4<∠1<∠3<∠2  D.∠4<∠1<∠3=∠23.(宁夏吴忠质检)如图,☉O中,=,∠ABC=70°.则∠BOC的度数为 (C)A.100°  B.90°  C.80°  D.70°4.(宁夏固原质检)如图,☉O中,OC⊥AB,∠APC=28°,则∠BOC的度数为              (D)A.14°  B.28°  C.42°  D.56°5.如图,☉O是△ABC的外接圆,已知∠ACB=60°,则∠ABO的大小为 (A)A.30°  B.40°  C.45°  D.50°6.(白银中考)如图,点A,B,C,D,E在☉O上,AB=CD,∠AOB=42°,则∠CED=              (D)A.48°  B.24°  C.22°  D.21°7.(宜昌中考)如图,C,D是☉O上直径AB两侧的两点,设∠ABC=25°,则∠BDC=              (D)A.85°  B.75°  C.70°  D.65°8.已知☉O的半径为10,圆心O到弦AB的距离为5,则弦AB所对圆周角的度数是(D)A.30°  B.60°  C.30°或150°  D.60°或120°9. (呼和浩特模拟)已知AB是☉O的直径,点C是半径OA的中点,过点C作DE⊥AB,交☉O于D,E两点,过点D作直径DF,连接AF,则∠DFA=　30°　. 10.(新疆伊犁模拟)如图,AB,CD为☉O内两条相交的弦,交点为E,且AB=CD,求证:AD∥BC.【证明】∵AB=CD,∴=,∴-=-,即=,∴∠B=∠A,∴AD∥BC.1.(内蒙古赤峰期末)如图,A,B,C,D四点均在☉O上,∠AOD=40°,弦DC的长等于半径,则∠B的度数为              (C)A.40°  B.45°  C.50°  D.55°2.(甘肃定西模拟)如图,AB为☉O的直径,C为☉O上一点,∠BOC=50°,AD∥OC,AD交☉O于点D,连接AC,CD,那么∠ACD=　40°　. 3.如图,A、B、C是☉O上的三点,以BC为一边,作∠CBD=∠ABC,过BC上一点P,作PE∥AB交BD于点E.若∠AOC=60°,BE=12,则点P到弦AB的距离为　6　. 4.(新疆哈密模拟)如图,点A,B,C,D,E都在☉O上,AC平分∠BAD,且AB∥CE,求证:=.【证明】∵AC平分∠BAD,∴∠BAC=∠DAC,∵AB∥CE,∴∠BAC=∠ACE,∴∠DAC=∠ACE,∴=.