初中数学4 圆周角和圆心角的关系课时作业

这是一份初中数学4 圆周角和圆心角的关系课时作业，共11页。
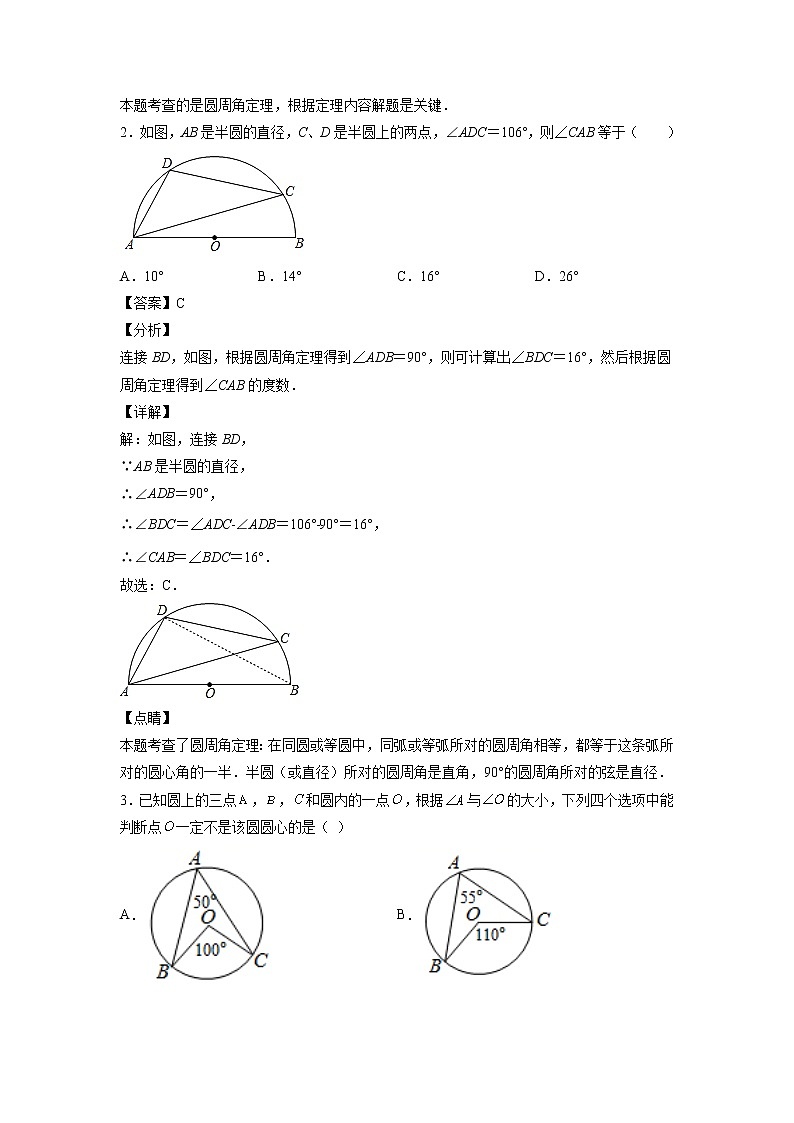
3.4.2 圆周角定理1．如图，AB是⊙O的直径，点C、D是⊙O上的点，OD⊥AC，连接DC，若∠COB＝30°，则∠ACD的度数为（　　）A．30° B．37.5° C．45° D．60°【答案】B【分析】由，得到，在直角三角形中，求得；根据，得到，即可得到正确答案．【详解】解：如下图：设AC与OD相交于点Ｅ∵∴ ∵ ∴∴ ∵∴ 故选：B【点睛】本题考查的是圆周角定理，根据定理内容解题是关键．2．如图，AB是半圆的直径，C、D是半圆上的两点，∠ADC＝106°，则∠CAB等于（　　）A．10° B．14° C．16° D．26°【答案】C【分析】连接BD，如图，根据圆周角定理得到∠ADB＝90°，则可计算出∠BDC＝16°，然后根据圆周角定理得到∠CAB的度数．【详解】解：如图，连接BD， ∵AB是半圆的直径，∴∠ADB＝90°，∴∠BDC＝∠ADC﹣∠ADB＝106°﹣90°＝16°，∴∠CAB＝∠BDC＝16°．故选：C．【点睛】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径．3．已知圆上的三点，，和圆内的一点，根据与的大小，下列四个选项中能判断点一定不是该圆圆心的是（ ）A． B．C． D．【答案】D【分析】利用圆周角定理判断即可．【详解】解：选项A，B，C中，∵∠BOC=2∠A，
∴选项A，B，C中，点O可能是圆心．
选项D中，∠BOC≠2∠A，
∴点O一定不是圆心，
故选：D．【点睛】本题考查圆周角定理，解题的关键是理解题意，灵活运用所学知识是解题的关键．4．如图，AD是△ABC的外接圆⊙O的直径，若∠BCA＝50°，则∠BAD＝（　　）A．30° B．40° C．50° D．60°【答案】B【分析】根据圆周角定理推论：直径所对圆周角为直角、同圆中等弧所对圆周角相等即可得到结论．【详解】解：是的外接圆的直径，点，，，在上，，，是的外接圆的直径，，，故选：．【点睛】本题考查了三角形的外接圆与外心，圆周角定理，由圆周角定理得到，是解题的关键．5．如图，等腰△ABC的顶角∠BAC＝50°，以AB为直径的半圆分别交BC，AC于点D，E．则的度数是（   ）A．45° B．50° C．60° D．75°【答案】B【分析】连接AD，根据等腰三角形的性质和圆心角的性质计算即可；【详解】连接AD，∵AB是直径，∴，∵，∴，∴的度数；故答案选B．【点睛】本题主要考查了等腰三角形的性质、圆心角、弧、弦的关系、圆周角定理，准确计算是解题的关键．6．如图，点A、B、C在⊙O上，，则的度数是（ ）A．40° B．84° C．42° D．30°【答案】C【分析】关键圆周角定理得出∠ACB=∠AOB，再求出答案即可．【详解】解：∵∠AOB=84°，∴∠ACB=∠AOB=42°，故选：C．【点睛】本题考查了圆周角定理和圆心角、弧、弦之间的关系等知识点，注意：一条弧所对的圆周角等于它所对的圆心角的一半．7．如图，是的内接三角形，若，则的度数等于（    ）
A．120° B．130° C．140° D．150°【答案】C【分析】欲求∠AOC，又已知圆周角，可利用圆周角与圆心角的关系求解．【详解】因为∠ABC和∠AOC是同一条弧AC所对的圆周角和圆心角，所以∠AOC=2∠ABC×70°=140°，故选：C.【点睛】本题考查圆周角定理，解题的关键是熟练掌握圆周角定理.8．如图，已知是的直径，过点的弦平行于半径，若的度数是，则的度数是（    ）A． B． C． D．【答案】A【分析】根据平行线的性质和圆周角定理计算即可；【详解】∵，，∴，∵，∴．故选A．【点睛】本题主要考查了圆周角定理、平行线的性质，准确计算是解题的关键．9．如图，四边形ADBC内接于⊙O，∠AOB＝122°，则∠ACB等于（　　）A．131° B．119° C．122° D．58°【答案】B【分析】根据同弧所对的圆心角是圆周角的一半即可求解．【详解】解：∵同弧所对的圆心角是圆周角的一半；∴根据圆内接四边形对角互补故选：B【点睛】此题考查的是圆周角定理的应用，掌握圆周角定理是解题的关键．10．如图，点A，B，C都在⊙O上，，则（    ）
A． B．C． D．【答案】B【分析】根据同弧所对的圆周角等于圆心角的一半即可求解．【详解】解：∵同弧所对的圆周角等于圆心角的一半，∴，，又∵，∴．故选：B．【点睛】本题考查了圆周角定理的应用，解题的关键是熟练掌握圆周角定理．二、填空题11．如图，一块直角三角板ABC的斜边AB与量角器的直径重合，点D对应的刻度值为50°，则∠BCD的度数为__________________．
【答案】【分析】如图，连接 先求解 再证明在以为圆心，半径为的圆上，再利用圆周角定理可得答案.【详解】解：如图，连接 点D对应的刻度值为50°，
直角三角板ABC的斜边AB与量角器的直径重合， 在以为圆心，半径为的圆上， 故答案为：【点睛】本题考查的是直角三角形的外接圆的性质，圆周角定理的应用，直角三角形斜边上的中线等于斜边的一半，灵活运用以上知识解题是解题的关键.12．如图，四边形ABCD内接于圆O，∠BOD＝108°，则∠BCD的度数是_______度．【答案】126【分析】先根据圆周角定理得到∠A＝∠BOD＝54°，然后根据圆内接四边形的性质求∠BCD的度数．【详解】∵∠BOD＝108°，∴∠A＝∠BOD＝54°，∴∠BCD＝180°﹣∠A＝126°．故答案是：126．【点睛】本题考查了圆内接四边形的性质，圆周角定理．在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．三、解答题13．如图，是上的四个点，．判断的形状，并证明你的结论．【答案】等边三角形，见解析【分析】利用圆周角定理可得∠BAC=∠CPB，∠ABC=∠APC，而∠APC=∠CPB=60°，所以∠BAC=∠ABC=60°，从而可判断△ABC的形状．【详解】解：△ABC是等边三角形．证明如下：由圆周角定理：∠BAC=∠CPB，∠ABC=∠APC∵∠APC＝∠CPB＝60°，∴∠BAC＝∠ABC＝60°，∴∠ACB＝180°－∠BAC－∠ABC＝180°－60°－60°＝60°．∴△ABC是等边三角形．【点睛】本题考查了圆周角定理、等边三角形的判定，解题的关键是掌握圆周角定理，正确求出∠ABC=∠BAC=60°．14．如图，以△ABC的边BC为直径的⊙O分别交AB、AC于点D、E，连结OD、OE，若∠A=65°，求∠DOE的度数．
【答案】【分析】连接 由为直径，求解 再利用圆周角定理可得答案.【详解】解：连接 由为直径，
则 【点睛】本题考查的是直径所对的圆周角是直角，圆周角定理，熟悉圆周角定理的应用是解题的关键.15．如图，⊙O的弦AB、DC的延长线相交于点E，∠AOD=150°，弧BC为50°，求∠ABD、∠AED的度数．【答案】【分析】根据圆周角定理直接求得，弧的度数等于圆心角的度数求得,根据圆周角定理求得，根据三角形的外角性质进而可得的度数．【详解】解：如图，连接，,，，弧BC为50°，，，，是的一个外角，，．【点睛】本题考查了圆周角定理，三角形的外角性质，掌握圆周角定理是解题的关键．