2022-2023学年河北省保定师范附属学校九年级（上）期末数学试卷

这是一份2022-2023学年河北省保定师范附属学校九年级（上）期末数学试卷，共28页。试卷主要包含了选择题，填空题，解答题等内容，欢迎下载使用。
2022-2023学年河北省保定师范附属学校九年级（上）期末数学试卷
一、选择题：（共16个小题，1-10题每题3分，11-16题每题2分，共42分）
1．（3分）方程（x﹣3）（x+4）＝0的解是（　　）
A．x＝3 B．x＝﹣4 C．x1＝3，x2＝﹣4 D．x1＝﹣3，x2＝4
2．（3分）已知，在Rt△ABC中，∠C＝90°，AB＝5，BC＝3，则sinA的值是（　　）
A．35 B．53 C．45 D．34
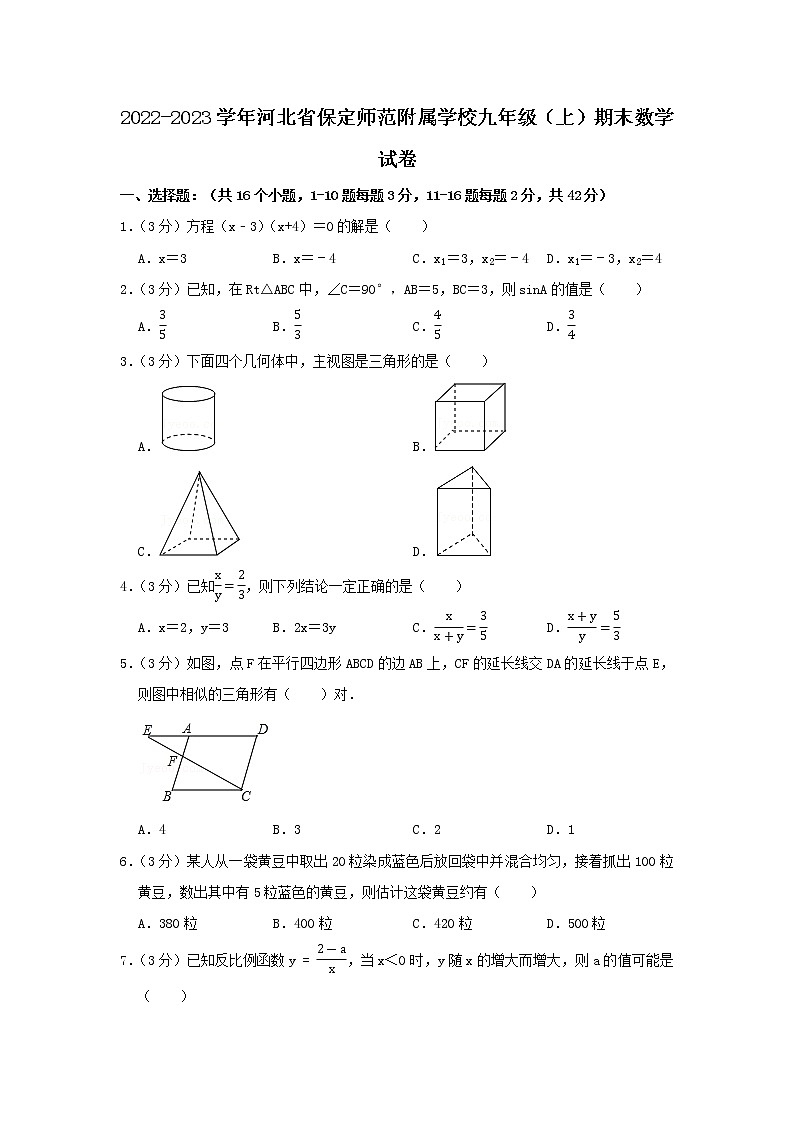
3．（3分）下面四个几何体中，主视图是三角形的是（　　）
A． B．
C． D．
4．（3分）已知xy=23，则下列结论一定正确的是（　　）
A．x＝2，y＝3 B．2x＝3y C．xx+y=35 D．x+yy=53
5．（3分）如图，点F在平行四边形ABCD的边AB上，CF的延长线交DA的延长线于点E，则图中相似的三角形有（　　）对．

A．4 B．3 C．2 D．1
6．（3分）某人从一袋黄豆中取出20粒染成蓝色后放回袋中并混合均匀，接着抓出100粒黄豆，数出其中有5粒蓝色的黄豆，则估计这袋黄豆约有（　　）
A．380粒 B．400粒 C．420粒 D．500粒
7．（3分）已知反比例函数y=2-ax，当x＜0时，y随x的增大而增大，则a的值可能是（　　）
A．3 B．2 C．1 D．﹣1
8．（3分）天猫某店铺第2季度的总销售额为662万元，其中4月份的销售额是200万元，设5、6月份的平均增长率为x，求此平均增长率可列方程为（　　）
A．200（1+x）2＝662
B．200+200（1+x）2＝662
C．200+200（1+x）+200（1+x）2＝662
D．200+200x+200（1+x）2＝662
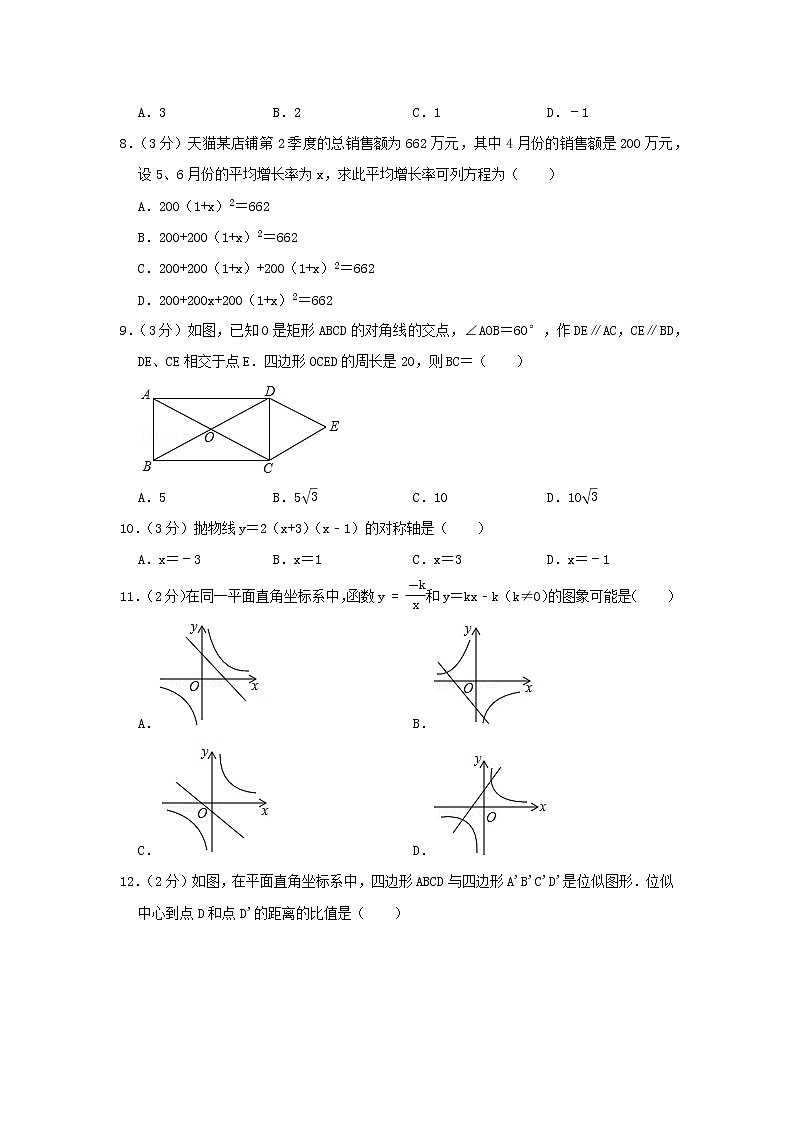
9．（3分）如图，已知O是矩形ABCD的对角线的交点，∠AOB＝60°，作DE∥AC，CE∥BD，DE、CE相交于点E．四边形OCED的周长是20，则BC＝（　　）

A．5 B．53 C．10 D．103
10．（3分）抛物线y＝2（x+3）（x﹣1）的对称轴是（　　）
A．x＝﹣3 B．x＝1 C．x＝3 D．x＝﹣1
11．（2分）在同一平面直角坐标系中，函数y=-kx和y＝kx﹣k（k≠0）的图象可能是（　　）
A． B．
C． D．
12．（2分）如图，在平面直角坐标系中，四边形ABCD与四边形A'B'C'D'是位似图形．位似中心到点D和点D'的距离的比值是（　　）

A．2 B．3 C．32 D．54
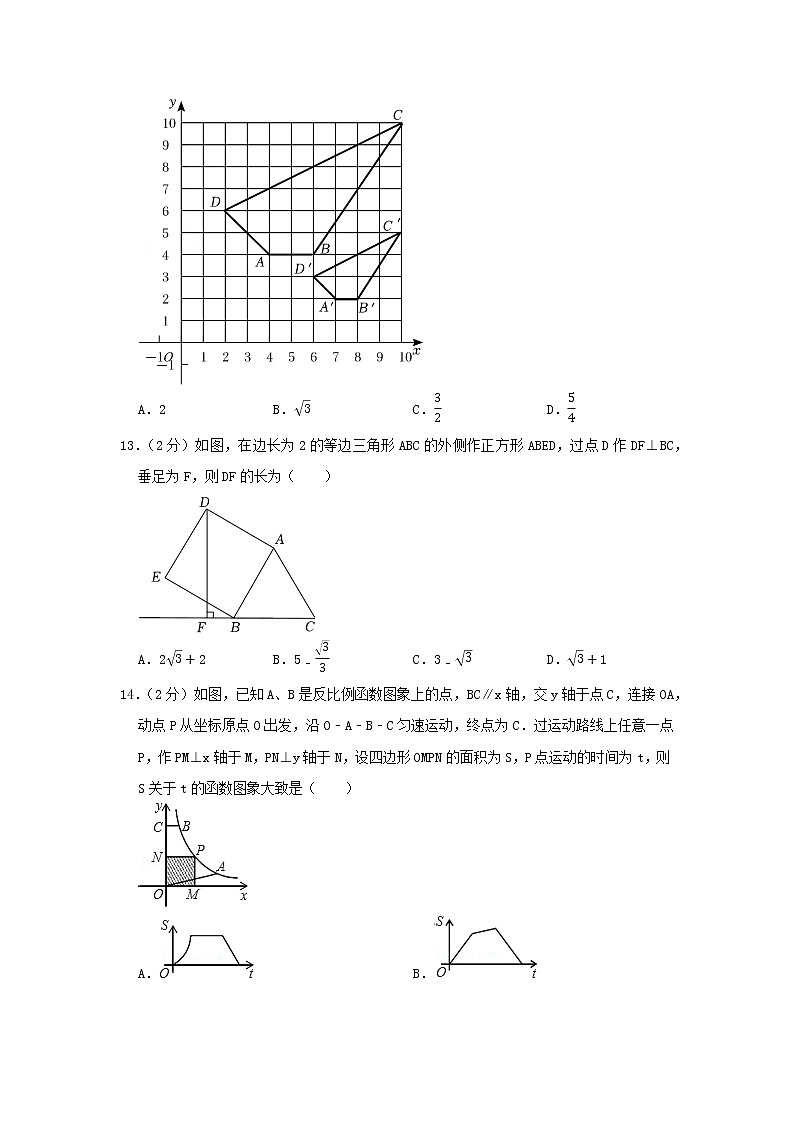
13．（2分）如图，在边长为2的等边三角形ABC的外侧作正方形ABED，过点D作DF⊥BC，垂足为F，则DF的长为（　　）

A．23+2 B．5-33 C．3-3 D．3+1
14．（2分）如图，已知A、B是反比例函数图象上的点，BC∥x轴，交y轴于点C，连接OA，动点P从坐标原点O出发，沿O﹣A﹣B﹣C匀速运动，终点为C．过运动路线上任意一点P，作PM⊥x轴于M，PN⊥y轴于N，设四边形OMPN的面积为S，P点运动的时间为t，则S关于t的函数图象大致是（　　）

A． B．
C． D．
15．（2分）抛物线y＝ax2+bx+c的大致图象如图所示，则下列说法中错误的是（　　）

A．abc＜0
B．3a+c＜0
C．当x＝t时，y＞0，若x＝t﹣4，则y＜0
D．a（x2﹣1）+b（x﹣1）＞0
16．（2分）如图，已知E是正方形ABCD中AB边延长线上一点，且AB＝BE，连接CE、DE，DE与BC交于点N，F是CE的中点，连接AF交BC于点M，连接BF．有如下结论：
①DN＝EN；
②△ABF∽△ECD；
③tan∠CED=13；
④S四边形BEFM＝2S△CMF．
其中正确的是（　　）

A．①②③ B．①②④ C．②③④ D．①②③④
二、填空题：（共3个小题，17、18题每题3分，19题4分，共10分）
17．（3分）若∠A是锐角，sinA=12，则∠A＝　 　．
18．（3分）如图，已知抛物线y＝ax2+bx+c与直线y＝kx+m交于A（﹣3，﹣1），B（0，3）两点．则关，于x的不等式ax2+bx+c≤kx+m的解集是 　 　．

19．（4分）（1）如图1，正方形ABCD的面积为a，延长边BC到点C1，延长边CD到点D1，延长边DA到点A1，延长边AB到点B1，使CC1＝BC，DD1＝CD，AA1＝DA，BB1＝AB，连接C1D1，D1A1，A1B1，B1C1，得到四边形A1B1C1D1，此时我们称四边形ABCD向外扩展了一次，若阴影部分的面积为S1，则S1＝　 　．（用含a的代数式表示）
（2）如图2，任意四边形ABCD面积为m，像（1）中那样将四边形ABCD向外进行两次扩展，第一次扩展成四边形A1B1C1D1，第二次扩展由四边形A1B1C1D1扩展成四边形A2B2C2D2，若阴影部分面积为S2，则S2＝　 　．（用含m的代数式表示）

三、解答题：（共7个小题，共68分）
20．（6分）计算：2cos45°﹣|1-2|+（13）﹣1-327．
21．（5分）用配方法解方程：x2﹣2x﹣8＝0．
22．（5分）若关于x的一元二次方程（k﹣1）x2+3x+k2﹣1＝0有一个解为x＝0，求k的值．
23．（8分）某博物馆展厅的俯视示意图如图1所示．嘉淇进入展厅后开始自由参观，每走到一个十字道口，她自己可能直行，也可能向左转或向右转，且这三种可能性均相同．

（1）求嘉淇走到王字道口A向北走的概率；
（2）补全图2的树状图，并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大．

24．（10分）如图，△ABC中∠A＝60°，∠B＝40°，点D、E分别在△ABC的边AB、AC上，且∠ADE＝80°．
（1）求证：△AED∽△ABC；
（2）若AD＝4，AB＝8，AE＝5，求CE的长．

25．（10分）如图，某幢大楼顶部有广告牌CD，小宇目高MA为1.89米，他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进15米、站在点B处，测得广告牌顶端点C的仰角为45°．（取3≈1.732，计算结果保留一位小数）
（1）求这幢大楼的高DH；
（2）求这块广告牌CD的高度．

26．（12分）某商场将一种每件成本价为10元的商品连续加价两次后，以每件24元件为定价售出，已知第二次加价的增长率比第一次加价的增长率多10%．
（1）求第一次加价的增长率；
（2）该商场在试销中发现，如果以定价售出，则每天可售出100个，如果销售单价每降低1元，销售量就可以增加10件，那么当销售单价为多少元时，该商场每天销售该商品获得的利润最大？最大利润是多少？
27．（12分）某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

（1）求水柱所在抛物线（第二象限部分）的函数表达式；
（2）主师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？
（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到24米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．

2022-2023学年河北省保定师范附属学校九年级（上）期末数学试卷
参考答案与试题解析
一、选择题：（共16个小题，1-10题每题3分，11-16题每题2分，共42分）
1．（3分）方程（x﹣3）（x+4）＝0的解是（　　）
A．x＝3 B．x＝﹣4 C．x1＝3，x2＝﹣4 D．x1＝﹣3，x2＝4
【分析】利用因式分解法解方程．
【解答】解：x﹣3＝0或x+4＝0，
所以x1＝3，x2＝﹣4．
故选：C．
【点评】本题考查了解一元二次方程﹣因式分解法：就是先把方程的右边化为0，再把左边通过因式分解化为两个一次因式的积的形式，那么这两个因式的值就都有可能为0，这就能得到两个一元一次方程的解，这样也就把原方程进行了降次，把解一元二次方程转化为解一元一次方程的问题了（数学转化思想）．
2．（3分）已知，在Rt△ABC中，∠C＝90°，AB＝5，BC＝3，则sinA的值是（　　）
A．35 B．53 C．45 D．34
【分析】根据正弦函数是对边比斜边，可得答案．
【解答】解：sinA=BCAB=35，
故选：A．
【点评】本题考查了锐角三角函数，利用正弦函数是对边比斜边是解题关键．
3．（3分）下面四个几何体中，主视图是三角形的是（　　）
A． B．
C． D．
【分析】主视图是从正面看所得到的平面图形，分别写出四个选项的主视图即可选出答案．
【解答】解：A、圆柱的主视图是长方形，故此选项错误；
B、立方体的主视图是正方形，故此选项错误；
C、四棱锥的主视图是三角形，故此选项正确；
D、三棱柱的主视图是长方形，故此选项错误；
故选：C．
【点评】此题主要考查了简单几何体的三视图，关键是掌握主视图所看的位置．
4．（3分）已知xy=23，则下列结论一定正确的是（　　）
A．x＝2，y＝3 B．2x＝3y C．xx+y=35 D．x+yy=53
【分析】根据比例的性质即两内项之积等于两外项之积分别对每一项进行分析即可得出答案．
【解答】解：∵xy=23，
∴3x＝2y，
∴A、B选项错误；
∵xy=23，
∴y=32x
∴xx+y=xx+32x=25，
∴C选项错误；
∵xy=23，
∴x+yy=xy+1=23+1=53，
∴D选项正确；
故选：D．
【点评】此题考查了比例的性质，熟练掌握两内项之积等于两外项之积是解题的关键，较简单．
5．（3分）如图，点F在平行四边形ABCD的边AB上，CF的延长线交DA的延长线于点E，则图中相似的三角形有（　　）对．

A．4 B．3 C．2 D．1
【分析】根据平行四边形的性质以及相似三角形的判定方法即可判断．
【解答】证明：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
由AF∥CD，可以推出△EAF∽△EDC，
由AE∥BC，可以推出△AEF∽△BCF，
则△EDC∽△CBF，
故图中相似的三角形有3对．
故选：B．
【点评】本题考查相似三角形的判定、平行四边形的性质等知识，熟练掌握相似三角形的判定方法是解题的关键，属于基础题．
6．（3分）某人从一袋黄豆中取出20粒染成蓝色后放回袋中并混合均匀，接着抓出100粒黄豆，数出其中有5粒蓝色的黄豆，则估计这袋黄豆约有（　　）
A．380粒 B．400粒 C．420粒 D．500粒
【分析】100粒黄豆中有5粒黄豆染成蓝色，说明在样本中有色的占到20%．而在总体中，蓝色的共有20粒，据此比例可求出黄豆总数．
【解答】解：依题意可得
估计这袋黄豆：20÷5100=400（粒）
故选：B．
【点评】本题考查了用样本的数据特征来估计总体的数据特征，利用样本中的数据对整体进行估算是统计学中最常用的估算方法．
7．（3分）已知反比例函数y=2-ax，当x＜0时，y随x的增大而增大，则a的值可能是（　　）
A．3 B．2 C．1 D．﹣1
【分析】直接利用反比例函数的性质得出2﹣a＜0，进而得出答案．
【解答】解：∵反比例函数y=2-ax，当x＜0时，y随x的增大而增大，
∴2﹣a＜0，
解得：a＞2．
故选：A．
【点评】此题主要考查了反比例函数的性质，正确得出2﹣a的符号是解题关键．
8．（3分）天猫某店铺第2季度的总销售额为662万元，其中4月份的销售额是200万元，设5、6月份的平均增长率为x，求此平均增长率可列方程为（　　）
A．200（1+x）2＝662
B．200+200（1+x）2＝662
C．200+200（1+x）+200（1+x）2＝662
D．200+200x+200（1+x）2＝662
【分析】主要考查增长率问题，一般用增长后的量＝增长前的量×（1+增长率），如果设利润平均每月的增长率为x，根据“第2季度的总销售额为662万元”，可得出方程．
【解答】解：设利润平均每月的增长率为x，
又知：第2季度的总销售额为662万元，其中4月份的销售额是200万元，
所以，可列方程为：200+200（1+x）+200（1+x）2＝662；
故选：C．
【点评】本题考查求平均变化率的方法．若设变化前的量为a，变化后的量为b，平均变化率为x，则经过两次变化后的数量关系为a（1±x）2＝b（当增长时中间的“±”号选“+”，当降低时中间的“±”号选“﹣”）．
9．（3分）如图，已知O是矩形ABCD的对角线的交点，∠AOB＝60°，作DE∥AC，CE∥BD，DE、CE相交于点E．四边形OCED的周长是20，则BC＝（　　）

A．5 B．53 C．10 D．103
【分析】首先根据两对边互相平行的四边形是平行四边形证明四边形OCED是平行四边形，再根据矩形的性质可得OC＝OD，即可利用一组邻边相等的平行四边形是菱形，再利用已知得出菱形的边长，即可得出答案．
【解答】解：∵DE∥AC，CE∥BD，
∴四边形OCED是平行四边形．
∵四边形ABCD是矩形，
∴AC＝BD，
∴OC＝OD，
∴四边形OCED是菱形；
∵四边形OCED的周长是20，
∴CO＝DO＝5，
∴BD＝10，
∵四边形ABCD是矩形，
∴OA＝OB，
又∵∠AOB＝60°，
∴△AOB是等边三角形，
∴OA＝OB＝OC＝AB＝5，
∴BC=102-52=53．
故选：B．
【点评】此题考查了菱形的判定与性质以及矩形的性质．此题难度不大，注意证得四边形CODE是菱形是解此题的关键．
10．（3分）抛物线y＝2（x+3）（x﹣1）的对称轴是（　　）
A．x＝﹣3 B．x＝1 C．x＝3 D．x＝﹣1
【分析】利用对称性，结合与x轴的两个交点坐标推导即可．
【解答】解：∵y＝2（x+3）（x﹣1）与x轴的交点坐标为（﹣3，0），（1，0），
∴对称轴为x=x1+x22
=-3+12
＝﹣1，
故选：D．
【点评】本题考查的是抛物线的对称轴，解题的关键是熟练掌握抛物线的对称轴公式．
11．（2分）在同一平面直角坐标系中，函数y=-kx和y＝kx﹣k（k≠0）的图象可能是（　　）
A． B．
C． D．
【分析】根据一次函数及反比例函数的图象与系数的关系作答．
【解答】解：A、从一次函数的图象过二、四象限知k＜0与反比例函数的图象﹣k＞0，即k＜0一致，故本选项正确；
B、从一次函数的图象知k＜0、﹣k＜0，相矛盾，故本选项错误；
C、从一次函数的图象知k＜0、﹣k＜0，且与反比例函数的图象k＞0相矛盾，故本选项错误；
D、从一次函数的图象知k＞0、﹣k＞0，相矛盾，故本选项错误；
故选：A．
【点评】本题主要考查了反比例函数的图象性质和一次函数的图象性质，重点是注意系数k的取值．
12．（2分）如图，在平面直角坐标系中，四边形ABCD与四边形A'B'C'D'是位似图形．位似中心到点D和点D'的距离的比值是（　　）

A．2 B．3 C．32 D．54
【分析】直接利用位似图形的性质得出位似中心，进而利用对应边的比值得出位似中心到点D和点D'的距离的比值．
【解答】解：如图所示：点P即为位似中心，位似中心到点D和点D'的距离的比值是：PD：PD′＝2：1＝2．
故选：A．

【点评】此题主要考查了位似变换，正确得出位似中心的位置是解题关键．
13．（2分）如图，在边长为2的等边三角形ABC的外侧作正方形ABED，过点D作DF⊥BC，垂足为F，则DF的长为（　　）

A．23+2 B．5-33 C．3-3 D．3+1
【分析】方法一：如图，延长DA、BC交于点G，利用正方形性质和等边三角形性质可得：∠BAG＝90°，AB＝2，∠ABC＝60°，运用解直角三角形可得AG＝23，DG＝2+23，再求得∠G＝30°，根据直角三角形性质得出答案．
方法二：过点E作EG⊥DF于点G，作EH⊥BC于点H，利用解直角三角形可得EH＝1，BH=3，再证明△BEH≌△DEG，可得DG＝BH=3，即可求得答案．
【解答】解：方法一：如图，延长DA、BC交于点G，

∵四边形ABED是正方形，
∴∠BAD＝90°，AD＝AB，
∴∠BAG＝180°﹣90°＝90°，
∵△ABC是边长为2的等边三角形，
∴AB＝2，∠ABC＝60°，
∴AG＝AB•tan∠ABC＝2×tan60°＝23，
∴DG＝AD+AG＝2+23，
∵∠G＝90°﹣60°＝30°，DF⊥BC，
∴DF=12DG=12×（2+23）＝1+3，
故选D．
方法二：如图，过点E作EG⊥DF于点G，作EH⊥BC于点H，
则∠BHE＝∠DGE＝90°，

∵△ABC是边长为2的等边三角形，
∴AB＝2，∠ABC＝60°，
∵四边形ABED是正方形，
∴BE＝DE＝2，∠ABE＝∠BED＝90°，
∴∠EBH＝180°﹣∠ABC﹣∠ABE＝180°﹣60°﹣90°＝30°，
∴EH＝BE•sin∠EBH＝2•sin30°＝2×12=1，BH＝BE•cos∠EBH＝2cos30°=3，
∵EG⊥DF，EH⊥BC，DF⊥BC，
∴∠EGF＝∠EHB＝∠DFH＝90°，
∴四边形EGFH是矩形，
∴FG＝EH＝1，∠BEH+∠BEG＝∠GEH＝90°，
∵∠DEG+∠BEG＝90°，
∴∠BEH＝∠DEG，
在△BEH和△DEG中，
∠BHE=∠DGE∠BEH=∠DEGBE=DE，
∴△BEH≌△DEG（AAS），
∴DG＝BH=3，
∴DF＝DG+FG=3+1，
故选：D．
【点评】本题考查了正方形的性质、等边三角形的性质、全等三角形的判定和性质、解直角三角形，题目的综合性很好，难度不大．
14．（2分）如图，已知A、B是反比例函数图象上的点，BC∥x轴，交y轴于点C，连接OA，动点P从坐标原点O出发，沿O﹣A﹣B﹣C匀速运动，终点为C．过运动路线上任意一点P，作PM⊥x轴于M，PN⊥y轴于N，设四边形OMPN的面积为S，P点运动的时间为t，则S关于t的函数图象大致是（　　）

A． B．
C． D．
【分析】当点P在AO上运动时，S＝PM×PN＝t2×sinαcosα=kOA2t2，其中kAO2常数，故函数的表达式为二次函数；当点P在AB段时，S＝k为常数；当点P在BC上时，S＝OC×（T﹣t）为一次函数；即可求解．
【解答】解：（1）当点P在AO上运动时，

设反比例函数的表达式为：y=kx，
设点A（m，n），则mn＝k，设∠AOM＝∠α，
则tanα=nm，则sinα=nm2+n2，cosα=mm2+n2，
则S＝PM×PN＝t2×sinαcosα=kOA2t2，其中kAO2常数，故函数的表达式为二次函数；
（2）当点P在AB段时，
S＝k为常数；
（3）当点P在BC上时，
设点P运动的总时间为T，则在BC上运动的时间为T﹣t，
S＝OC×（T﹣t）为一次函数；
故选：A．
【点评】本题考查的是动点图象问题，涉及到二次函数、一次函数、解直角三角形等知识，此类问题关键是：弄清楚不同时间段，图象和图形的对应关系，进而求解．
15．（2分）抛物线y＝ax2+bx+c的大致图象如图所示，则下列说法中错误的是（　　）

A．abc＜0
B．3a+c＜0
C．当x＝t时，y＞0，若x＝t﹣4，则y＜0
D．a（x2﹣1）+b（x﹣1）＞0
【分析】利用抛物线开口向上得到a＜0，利用抛物线的对称轴方程得b＝﹣2a＞0，利用抛物线与y轴的交点位置得到c＞0，则可对①进行判断；利用抛物线的对称性得到抛物线与x轴的另一个交点坐标为（﹣1，0），代入解析式可判断②，求出t﹣4的范围可判断③，由题意可得当x＝1时，y有最大值为a+b+c，可判断④．
【解答】解：∵抛物线开口向下，
∴a＜0，
∵抛物线的对称轴为直线x=-b2a=1，
∴b＝﹣2a＞0，
∵抛物线与y轴的交点在y轴的正半轴，
∴c＞0，
∴abc＜0，故选项A不合题意；
∵x＝3时，y＜0，对称轴为x＝1，
∴x＝﹣1时，y＜0，
∴a﹣b+c＜0，
∴a+2a+c＜0，
∴3a+c＜0，故选项B不合题意；
∵当x＝t时，y＞0，
∴|t﹣1|＜2，
∴﹣1＜t＜3，
∴﹣5＜t﹣4＜﹣1，
∴当x＝t﹣4时，y＜0，故选项C不合题意；
∵当x＝1时，y有最大值为a+b+c，
∴ax2+bx+c﹣（a+b+c）≤0，
∴a（x2﹣1）+b（x﹣1）≤0，故选项符合题意；
故选：D．
【点评】本题考查二次函数的图象与性质，解题的关键是熟练掌握基本知识，学会利用数形结合的思想思考问题，属于中考常考题型．
16．（2分）如图，已知E是正方形ABCD中AB边延长线上一点，且AB＝BE，连接CE、DE，DE与BC交于点N，F是CE的中点，连接AF交BC于点M，连接BF．有如下结论：
①DN＝EN；
②△ABF∽△ECD；
③tan∠CED=13；
④S四边形BEFM＝2S△CMF．
其中正确的是（　　）

A．①②③ B．①②④ C．②③④ D．①②③④
【分析】证明△NCD∽△NBE，根据相似三角形的性质列出比例式，得到DN＝EN，判断①；根据两边对应成比例、夹角相等的两个三角形相似判断②；FG⊥AE于G，根据等腰直角三角形的性质、正切的定义求出tan∠FAG，根据相似三角形的性质判断③；根据三角形的面积公式计算，判断④．
【解答】解：∵四边形ABCD为正方形，AB＝BE，
∴AB＝CD＝BE，AB∥CD，
∴△NCD∽△NBE，
∴NDNE=CDBE=1，
∴DN＝EN，故①结论正确；
∵∠CBE＝90°，BC＝BE，F是CE的中点，
∴∠BCE＝45°，BF=12CE=22BE，FB＝FE，BF⊥EC，
∴∠BCE＝90°+45°＝135°，∠FBE＝45°，
∴∠ABF＝135°，
∴∠ABF＝∠ECD，
∵DCCE=22，BEAB=22，
∴DCCE=BEAB，
∴△ABF∽△ECD，故②结论正确；
作FG⊥AE于G，则FG＝BG＝GE，
∴FGAG=13，
∴tan∠FAG=FGAG=13，
∵△ABF∽△ECD，
∴∠CED＝∠FBG，
∴tan∠CED=13，故③结论正确；
∵tan∠FAG=13，
∴BMAB=13，
∴BMMC=12，
∴S△FBM=12S△FCM，
∵F是CE的中点，
∴S△FBC＝S△FBE，
∴S四边形BEFM＝2S△CMF，故④结论正确；
故选：D．

【点评】本题考查的是相似三角形的判定和性质、三角形的面积计算，掌握相似三角形的判定定理和性质定理、三角形的面积公式是解题的关键．
二、填空题：（共3个小题，17、18题每题3分，19题4分，共10分）
17．（3分）若∠A是锐角，sinA=12，则∠A＝　30°　．
【分析】根据特殊角三角函数值解答即可．
【解答】解：∵sinA=12，并且∠A是锐角，
∴∠A＝30°，
故答案为：30°．
【点评】本题主要考查特殊三角函数值，牢记特殊三角函数值是关键．
18．（3分）如图，已知抛物线y＝ax2+bx+c与直线y＝kx+m交于A（﹣3，﹣1），B（0，3）两点．则关，于x的不等式ax2+bx+c≤kx+m的解集是 　x≤﹣3或x≥0　．

【分析】根据图象写出抛物线在直线下方部分的x的取值范围即可．
【解答】解：∵抛物线y＝ax2+bx+c与直线y＝kx+m交于A（﹣3，﹣1），B（0，3）两点，
∴不等式ax2+bx+c≤kx+m的解集是x≤﹣3或x≥0．
故答案为：x≤﹣3或x≥0．
【点评】本题考查了二次函数与不等式的关系，能利用数形结合求不等式的解集是解题的关键．
19．（4分）（1）如图1，正方形ABCD的面积为a，延长边BC到点C1，延长边CD到点D1，延长边DA到点A1，延长边AB到点B1，使CC1＝BC，DD1＝CD，AA1＝DA，BB1＝AB，连接C1D1，D1A1，A1B1，B1C1，得到四边形A1B1C1D1，此时我们称四边形ABCD向外扩展了一次，若阴影部分的面积为S1，则S1＝　4a　．（用含a的代数式表示）
（2）如图2，任意四边形ABCD面积为m，像（1）中那样将四边形ABCD向外进行两次扩展，第一次扩展成四边形A1B1C1D1，第二次扩展由四边形A1B1C1D1扩展成四边形A2B2C2D2，若阴影部分面积为S2，则S2＝　24m　．（用含m的代数式表示）

【分析】（1）分析图形可发现规律，周边阴影区域的总面积为中间四边形ABCD的面积的4倍，根据规律计算即可；
（2）根据（1）中的规律进行二次计算即可．
【解答】解：（1）∵正方形ABCD的面积为a，CC1＝BC，DD1＝CD，AA1＝DA，BB1＝AB，
∴△A1DD1，△D1CC1，△C1BB1，△B1AA1这4个三角形为全等的直角三角形，
∴CC1＝BC=a，CD1＝2a，
∴△C1CD1的面积为12×a×2a=a，
∴阴影区域的面积S1为4a，
故答案为：4a；
（2）连A1B，AC，BD，AD1，DC1，B1C，如图：

∵四边形ABCD的面积为m，CC1＝BC，DD1＝CD，AA1＝DA，BB1＝AB，
∴S△BCD=S△DCC1=12S△D1CC1，
S△BAD=S△BAA1=12S△B1AA1，
∴S△D1CC1+S△B1AA1=2S△BCD+2S△BAD＝2m，
同理，S△A1DD1+S△C1BB1=2m
∴可以得到如下规律，扩展了一次后得到的四个小三角形的面积之和为原四边形面积的4倍，
∴S四边形A1B1C1D1=5m，
根据得到的规律可以直接得出第二次扩展后得到的四个大三角形的面积之和为20m，
∴第二次扩展由四边形A1B1C1D1扩展成四边形A2B2C2D2，的面积为25m，
∴阴影部分面积为S2为24m．
故答案为：24m．
【点评】本题主要考查三角形的面积，面积和等积变形等知识点的应用，根据得出的三角形面积得出规律是解答此题的关键．
三、解答题：（共7个小题，共68分）
20．（6分）计算：2cos45°﹣|1-2|+（13）﹣1-327．
【分析】原式利用特殊角的三角函数值，绝对值的代数意义，负整数指数幂法则，以及立方根定义计算即可求出值．
【解答】解：原式＝2×22-（2-1）+3﹣3
=2-2+1
＝1．
【点评】此题考查了实数的运算，负整数指数幂，以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．
21．（5分）用配方法解方程：x2﹣2x﹣8＝0．
【分析】方程移项后，利用完全平方公式配方，开方即可求出解．
【解答】解：方程移项得：x2﹣2x＝8，
配方得：x2﹣2x+1＝9，即（x﹣1）2＝9，
开方得：x﹣1＝3或x﹣1＝﹣3，
解得：x1＝4，x2＝﹣2．
【点评】此题考查了解一元二次方程﹣配方法，熟练掌握完全平方公式是解本题的关键．
22．（5分）若关于x的一元二次方程（k﹣1）x2+3x+k2﹣1＝0有一个解为x＝0，求k的值．
【分析】把x＝0代入一元二次方程k2﹣1＝0，再解关于k的方程，然后根据一元二次方程的定义确定满足条件的k的值．
【解答】解：把x＝0代入一元二次方程（k﹣1）x2+3x+k2﹣1＝0得k2﹣1＝0，
解得k1＝1，k2＝1，
因为k﹣1≠0，
所以k＝﹣1．
【点评】本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解．也考查了一元二次方程的定义．
23．（8分）某博物馆展厅的俯视示意图如图1所示．嘉淇进入展厅后开始自由参观，每走到一个十字道口，她自己可能直行，也可能向左转或向右转，且这三种可能性均相同．

（1）求嘉淇走到王字道口A向北走的概率；
（2）补全图2的树状图，并分析嘉淇经过两个十字道口后向哪个方向参观的概率较大．

【分析】（1）直接由概率公式求解即可；
（2）补全树状图，共有9种等可能的结果，嘉淇经过两个十字道口后向西参观的结果有3种，向南参观的结果有2种，向北参观的结果有2种，向东参观的结果有2种，由概率公式求解即可．
【解答】解：（1）嘉淇走到十字道口A向北走的概率为13；
（2）补全树状图如下：


共有9种等可能的结果，嘉淇经过两个十字道口后向西参观的结果有3种，向南参观的结果有2种，向北参观的结果有2种，向东参观的结果有2种，
∴向西参观的概率为39=13，向南参观的概率＝向北参观的概率＝向东参观的概率=29，
∴向西参观的概率大．
【点评】本题考查的是用列表法或画树状图法求概率，正确记忆概率＝所求情况数与总情况数之比是解题关键．
24．（10分）如图，△ABC中∠A＝60°，∠B＝40°，点D、E分别在△ABC的边AB、AC上，且∠ADE＝80°．
（1）求证：△AED∽△ABC；
（2）若AD＝4，AB＝8，AE＝5，求CE的长．

【分析】（1）根据两角对应相等两三角形相似即可证明．
（2）利用相似三角形的性质解决问题即可．
【解答】（1）证明：∵∠A＝60°，∠B＝40°
∴∠C＝80°
∵∠A＝∠A，∠ADE＝∠C
∴△AED∽△ABC

（2）解：由（1）得△AED∽△ABC
∴ADAC=AEAB
∵AD＝4，AB＝8，AE＝5
∴AC=325
∵CE＝AC﹣AE
∴CE=325-5=75．
【点评】本题考查相似三角形的判定和性质，解题的关键是熟练掌握基本知识，属于中考常考题型．
25．（10分）如图，某幢大楼顶部有广告牌CD，小宇目高MA为1.89米，他站在立在离大楼45米的A处测得大楼顶端点D的仰角为30°；接着他向大楼前进15米、站在点B处，测得广告牌顶端点C的仰角为45°．（取3≈1.732，计算结果保留一位小数）
（1）求这幢大楼的高DH；
（2）求这块广告牌CD的高度．

【分析】在Rt△DME与Rt△CNE；应利用ME﹣NE＝AB＝15构造方程关系式，进而可解即可求出答案．
【解答】解：（1）在Rt△DME中，ME＝AH＝45米；
tan30°=DEME，得DE＝45×33=15×1.732＝25.98米；
又因为EH＝MA＝1.89米，
因而大楼DH＝DE+EH＝25.98+1.89＝27.87≈27.9米；

（2）又在Rt△CNE中，NE＝45﹣15＝30米，
由tan45°=CENE，得CE＝NE＝30米；
因而广告牌CD＝CE﹣DE＝30﹣25.98≈4.0米；
答：楼高DH为27.9米，广告牌CD的高度为4.0米．
【点评】本题考查解直角三角形的应用﹣仰角俯角问题，锐角三角函数等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型．
26．（12分）某商场将一种每件成本价为10元的商品连续加价两次后，以每件24元件为定价售出，已知第二次加价的增长率比第一次加价的增长率多10%．
（1）求第一次加价的增长率；
（2）该商场在试销中发现，如果以定价售出，则每天可售出100个，如果销售单价每降低1元，销售量就可以增加10件，那么当销售单价为多少元时，该商场每天销售该商品获得的利润最大？最大利润是多少？
【分析】（1）设第一次加价的增长率为x，根据成本价为10元的商品连续加价两次后，以每件24元件为定价售出，可得关于x的一元二次方程，求解并根据问题实际作出取舍；
（2）设当销售单价为m元/个时，获得的利润为y元，根据利润等于每件的利润乘以销售量，列出y关于m的函数关系式，将其写成顶点式，根据二次函数的性质可得答案．
【解答】解：（1）设第一次加价的增长率为x，由题意得：
10（1+x）（1+x+10%）＝24，
解得：x1＝0.5＝50%，x2＝﹣2.6（不合题意，舍）．
∴第一次加价的增长率为50%．
（2）设当销售单价为m元/个时，获得的利润为y元，由题意得：
y＝（m﹣10）[100+10（24﹣m）]
＝﹣10m2+440m﹣3400
＝﹣10（m﹣22）2+1440，
∵﹣10＜0，
∴当m＝22时，y取得最大值为1440．
∴当销售单价为22元时，该商场每天销售该商品获得的利润最大，最大利润是1440元．
【点评】本题考查了一元二次方程和二次函数在增长率问题和销售问题中的应用，理清题中的数量关系并熟练掌握二次函数的性质是解题的关键．
27．（12分）某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系．

（1）求水柱所在抛物线（第二象限部分）的函数表达式；
（2）主师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？
（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到24米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度．
【分析】（1）根据顶点坐标可设二次函数的顶点式，代入点（﹣8，0），求出a值，此题得解；
（2）利用二次函数图象上点的坐标特征，求出当y＝1.8时x的值，由此即可得出结论；
（3）利用二次函数图象上点的坐标特征可求出抛物线与y轴的交点坐标，由抛物线的形状不变可设改造后水柱所在抛物线（第一象限部分）的函数表达式为y=-15x2+bx+165，代入点（12，0）可求出b值，再利用配方法将二次函数表达式变形为顶点式，即可得出结论．
【解答】解：（1）∵关于y轴对称，
∴第二象限抛物线的顶点坐标为（﹣3，5），
设水柱所在抛物线（第二象限部分）的函数表达式为y＝a（x+3）2+5（a≠0），
将（﹣8，0）代入y＝a（x+3）2+5，得：25a+5＝0，
解得：a=-15，
∴水柱所在抛物线（第二象限部分）的函数表达式为y=-15（x+3）2+5（﹣8＜x＜0）；
（2）当y＝1.8时，有-15（x+3）2+5＝1.8，
解得：x1＝﹣7，x2＝1，
∴为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心7米以内；
（3）当x＝0时，y=-15（x+3）2+5=165，
设改造后水柱所在抛物线（第二象限部分）的函数表达式为y=-15x2+bx+165，
∵该函数图象过点（﹣12，0），
∴0=-15×（﹣12）2+（﹣12）b+165，
解得：b=-3215，
∴改造后水柱所在抛物线（第二象限部分）的函数表达式为y=-15x2-3215x+165=-15（x+163）2+809，
∴扩建改造后喷水池水柱的最大高度为809 米．
【点评】本题考查了二次函数的应用，掌握待定系数法求二次函数解析式以及二次函数图象上点的坐标特征是解题的关键．