
2022-2023学年福建省福州市中考数学专项突破仿真模拟卷(一模二模)含解析
展开2022-2023学年福建省福州市中考数学专项突破仿真模拟卷
(一模)
一、选一选:本大题共10小题,每小题3分,共30分,在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或没有涂均为零分.
1. 据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要5300万美元,“5300万”用科学记数法可表示( )
A. 5.3×103 B. 5.3×104 C. 5.3×107 D. 5.3×108
2. 某潜水艇停在海面下500米处,先下降200米,又上升130米,这时潜水艇停在海面下多少米处( )
A. 430 B. 530 C. 570 D. 470
3. 如图,已知直线、被直线所截,,E是直线右边任意一点(点E没有在直线,上),设,.下列各式:①,②,③,④,度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
4. 如图,是一个正方体纸盒的展开图,若在其中三个正方形A,B,C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A,B,C中的三个数依次是( )
A. 1,﹣3,0 B. 0,﹣3,1 C. ﹣3,0,1 D. ﹣3,1,0
5. 下列运算正确的是( )
A. (π﹣3)0=1 B. =±3 C. 2﹣1=﹣2 D. (﹣a2)3=a6
6. 在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
7. 一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
A. 300° B. 150° C. 120° D. 75°
8. 若α、β为方程2x2-5x-1=0两个实数根,则的值为( )
A. -13 B. 12 C. 14 D. 15
9. 如图,P(m,m)是反比例函数y=在象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )
A. B. 3 C. D.
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=;⑤S四边形CDEF=S△ABF,其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
二、填 空 题:本大题共6小题,每小题3分,共18分,请将结果直接填写在答题卡对应的横线上.
11. 数学家发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将实数对(﹣2,3)放入其中得到实数m,再将实数对(m,1)放入其中后,得到的实数是_____.
12. 一个自行车轮胎,若把它安装在前轮,则自行车行驶5000 km后报废;若把它安装在后轮,则自行车行驶3000km后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶___km.
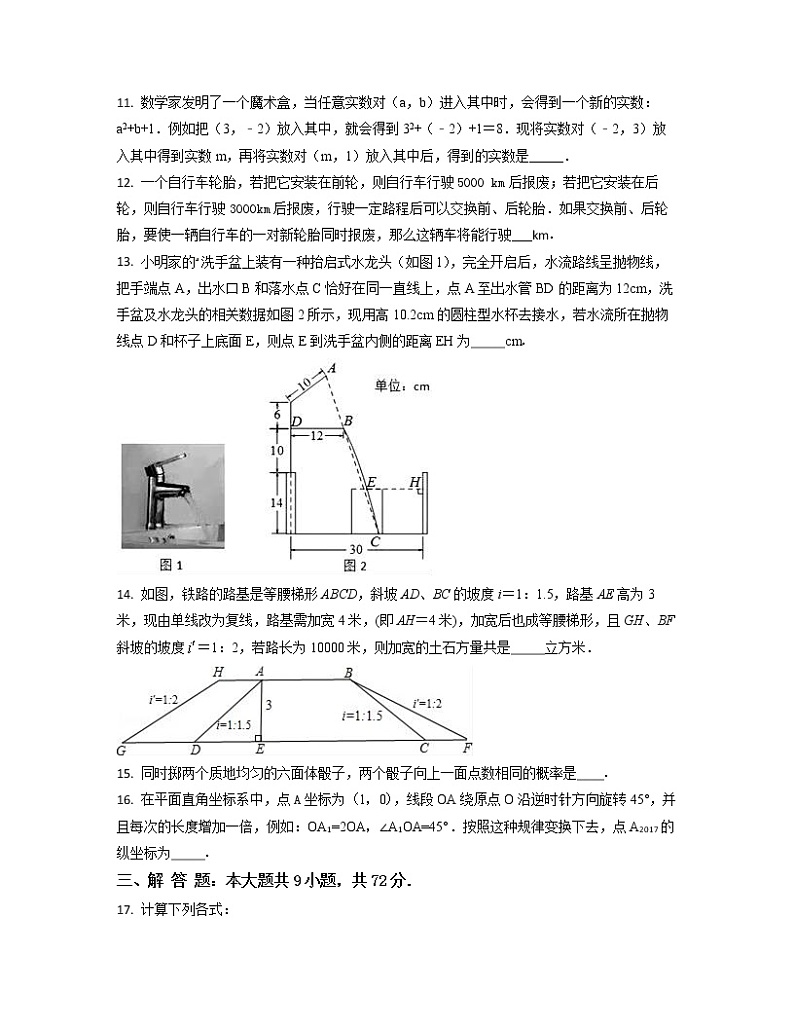
13. 小明家的洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线点D和杯子上底面E,则点E到洗手盆内侧的距离EH为_____cm.
14. 如图,铁路的路基是等腰梯形ABCD,斜坡AD、BC的坡度i=1:1.5,路基AE高为3米,现由单线改为复线,路基需加宽4米,(即AH=4米),加宽后也成等腰梯形,且GH、BF斜坡的坡度=1:2,若路长为10000米,则加宽的土石方量共是_____立方米.
15. 同时掷两个质地均匀的六面体骰子,两个骰子向上一面点数相同的概率是____.
16. 在平面直角坐标系中,点A坐标为(1,0),线段OA绕原点O沿逆时针方向旋转45°,并且每次的长度增加一倍,例如:OA1=2OA,∠A1OA=45°.按照这种规律变换下去,点A2017的纵坐标为_____.
三、解 答 题:本大题共9小题,共72分.
17. 计算下列各式:
(1) ;
(2) ;
(3)
(4) .
18. 解没有等式组:,并将解集在数轴上表示出来.
19. 图(a)是正方形纸板制成的一副七巧板.
(1)请你在图(a)中给它的每一小块用①~⑦编号(编号直接标在每一小块对应图形内部的空白处;每小块只能与一个编号对应,每个编号只能和一个小块对应),并同时满足以下三个条件:
条件1:编号为①~③的三小块可以拼成一个轴对称图形;
条件2:编号为④~⑥的三小块可以拼成一个对称图形;
条件3:编号为⑦的小块是对称图形.
(2)请你在图(b)中画出编号为①~③的三小块拼出的轴对称图形;在图(c)中画出编号为④~⑥的三小块拼出的对称图形.(注意:没有编号没有得分)
20. 近几年,随着电子商务的发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份
2014
2015
2016
2017(预计)
快递件总量(亿件)
140
207
310
450
电商包裹件(亿件)
98
153
235
351
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
21. 如图,直线EF交⊙O于A、B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
(1)求证:AD平分∠CAE;
(2)若DE=4cm,AE=2cm,求⊙O的半径.
22. 某学校要制作一批工作的宣传材料.甲公司提出:每份材料收费10元,另收1000元的版面设计费;乙公司提出:每份材料收费20元,没有收版面设计费.请你帮助该学校选择制作.
23. 已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k何值,方程总有两个没有相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象没有第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的整数值.
24. 如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
25. 建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y=x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2的函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若没有能,请说明理由.
2022-2023学年福建省福州市中考数学专项突破仿真模拟卷
(一模)
一、选一选:本大题共10小题,每小题3分,共30分,在下列各小题中,均给出四个答案,其中有且只有一个正确答案,请将正确答案的字母代号在答题卡上涂黑,涂错或没有涂均为零分.
1. 据悉,超级磁力风力发电机可以大幅度提升风力发电效率,但其造价高昂,每座磁力风力发电机,其建造花费估计要5300万美元,“5300万”用科学记数法可表示为( )
A. 5.3×103 B. 5.3×104 C. 5.3×107 D. 5.3×108
【正确答案】C
【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的值与小数点移动的位数相同.当原数值>1时,n是正数;当原数的值<1时,n是负数.
【详解】解:5300万=53000000=.
故选C.
在把一个值较大的数用科学记数法表示为的形式时,我们要注意两点:①必须满足:;②比原来的数的整数位数少1(也可以通过小数点移位来确定).
2. 某潜水艇停在海面下500米处,先下降200米,又上升130米,这时潜水艇停在海面下多少米处( )
A. 430 B. 530 C. 570 D. 470
【正确答案】C
【详解】根据题意,由下降200米用-200米表示,上升130米用+130米表示,
可以列式为:(-500)+(-200)+130=-570米,即这时潜水艇停在海面下570米.
故选:C.
3. 如图,已知直线、被直线所截,,E是直线右边任意一点(点E没有在直线,上),设,.下列各式:①,②,③,④,的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
【正确答案】A
【分析】根据点E有3种可能位置,分情况进行讨论,依据平行线的性质以及三角形外角性质进行计算求解即可.
【详解】解:(1)如图,由AB∥CD,可得∠AOC=∠DCE1=β,
∵∠AOC=∠BAE1+∠AE1C,
∴∠AE1C=β-α.
(2)如图,过E2作AB平行线,则由AB∥CD,可得∠1=∠BAE2=α,∠2=∠DCE2=β,
∴∠AE2C=α+β.
(3)当点E在CD的下方时,同理可得,∠AEC=α-β.
综上所述,∠AEC的度数可能为β-α,α+β,α-β.
即①α+β,②α-β,③β-α,都成立.
故选A.
本题主要考查了平行线性质的运用,解题时注意:两直线平行,同位角相等;两直线平行,内错角相等.
4. 如图,是一个正方体纸盒的展开图,若在其中三个正方形A,B,C中分别填入适当的数,使得它们折成正方体后相对的面上两个数互为相反数,则填入正方形A,B,C中的三个数依次是( )
A. 1,﹣3,0 B. 0,﹣3,1 C. ﹣3,0,1 D. ﹣3,1,0
【正确答案】A
【详解】使得它们折成正方体后相对的面上两个数互为相反数,则A与-1,B与3;C与0互为相反数.
解答:解:根据以上分析:填入正方形A,B,C中的三个数依次是1,-3,0.
故选A.
5. 下列运算正确的是( )
A. (π﹣3)0=1 B. =±3 C. 2﹣1=﹣2 D. (﹣a2)3=a6
【正确答案】A
【详解】根据零次幂的性质a0=1(a≠0),可知(π﹣3)0=1,故正确,符合题意;
根据算术平方根意义,可知=3,故没有正确,没有符合题意;
根据负整指数的性质,可知2﹣1=,故没有正确,没有符合题意;
根据幂的乘方和积的乘方,可知(﹣a2)3=-a6,故没有正确,没有符合题意.
故选A.
6. 在2016年泉州市初中体育中考中,随意抽取某校5位同学一分钟跳绳的次数分别为:158,160,154,158,170,则由这组数据得到的结论错误的是( )
A. 平均数为160 B. 中位数为158 C. 众数为158 D. 方差为20.3
【正确答案】D
【详解】解:A.平均数为(158+160+154+158+170)÷5=160,正确,故本选项没有符合题意;
B.按照从小到大的顺序排列为154,158,158,160,170,位于中间位置的数为158,故中位数为158,正确,故本选项没有符合题意;
C.数据158出现了2次,次数至多,故众数为158,正确,故本选项没有符合题意;
D.这组数据的方差是S2=[(154﹣160)2+2×(158﹣160)2+(160﹣160)2+(170﹣160)2]=28.8,错误,故本选项符合题意.
故选D.
点睛:本题考查了众数、平均数、中位数及方差,解题的关键是掌握它们的定义,难度没有大.
7. 一个扇形的弧长是10πcm,面积是60πcm2,则此扇形的圆心角的度数是( )
A. 300° B. 150° C. 120° D. 75°
【正确答案】B
【分析】利用扇形面积公式1求出R的值,再利用扇形面积公式2计算即可得到圆心角度数.
【详解】∵一个扇形的弧长是10πcm,面积是60πcm2,
∴S=Rl,即60π=×R×10π,解得:R=12,
∴S=60π=,
解得:n=150°,
故选B.
8. 若α、β为方程2x2-5x-1=0的两个实数根,则的值为( )
A. -13 B. 12 C. 14 D. 15
【正确答案】B
【详解】解:∵α、β为方程2x2-5x-1=0的两个实数根,
∴,,
因此可得2α2=5α+1,
代入2α2+3αβ+5β
=5α+1+3αβ+5β
=5(α+β)+3αβ+1
=5×+3×(-)+1
=12;
故选B.
此题主要考查了一元二次方程根与系数的关系,关键是利用一元二次方程的一般式,得到根与系数的关系x1+x2=-,x1·x2=,然后变形代入即可.
9. 如图,P(m,m)是反比例函数y=在象限内的图象上一点,以P为顶点作等边△PAB,使AB落在x轴上,则△POB的面积为( )
A. B. 3 C. D.
【正确答案】D
【详解】试题解析:作PD⊥OB,∵P(m,m)是反比例函数在象限内的图象上一点,∴,解得:m=3,∴PD=3,∵△ABP是等边三角形,∴BD=PD=,∴S△POB=OB•PD=(OD+BD)•PD=,故选D.
10. 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,分析下列五个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=;⑤S四边形CDEF=S△ABF,其中正确的结论有( )
A. 5个 B. 4个 C. 3个 D. 2个
【正确答案】B
【详解】过D作DM∥BE交AC于N,∵四边形ABCD是矩形,∴AD∥BC,∠ABC=90°,AD=BC,∵BE⊥AC于点F,∴∠EAC=∠ACB,∠ABC=∠AFE=90°,∴△AEF∽△CAB,故①正确;
∵AD∥BC,∴△AEF∽△CBF,∴,∵AE=AD=BC,∴,∴CF=2AF,故②正确,
∵DE∥BM,BE∥DM,∴四边形BMDE是平行四边形,∴BM=DE=BC,∴BM=CM,∴CN=NF,∵BE⊥AC于点F,DM∥BE,∴DN⊥CF,∴DF=DC,故③正确;
设AD=a,AB=b,易知△BAE∽△ADC,有,即
∵tan∠CAD=,∴tan∠CAD=,故④错误;
∵△AEF∽△CBF,∴,∴S△AEF=S△ABF,S△ABF=S矩形ABCD,∵S△ABE=S矩形ABCD,S△ACD=S矩形ABCD,∴S△AEF=S四边形ABCD,又∵S四边形CDEF=S△ACD﹣S△AEF=S矩形ABCD﹣S矩形ABCD=S矩形ABCD,∴S四边形CDEF=S△ABF,故⑤正确;
故选B.
考点:1.相似三角形的判定与性质;2.矩形的性质;3.综合题.
二、填 空 题:本大题共6小题,每小题3分,共18分,请将结果直接填写在答题卡对应的横线上.
11. 数学家发明了一个魔术盒,当任意实数对(a,b)进入其中时,会得到一个新的实数:a2+b+1.例如把(3,﹣2)放入其中,就会得到32+(﹣2)+1=8.现将实数对(﹣2,3)放入其中得到实数m,再将实数对(m,1)放入其中后,得到的实数是_____.
【正确答案】66
【分析】根据题中规定的运算,先求m的值,再求(m,1)的值.
【详解】由(a,b)=a2+b+1,得
(-2,3)=(-2)2+3+1=8,
所以,m=8,
(m,1)=(8,1)=82+1+1=66,
故答案为66.
12. 一个自行车轮胎,若把它安装在前轮,则自行车行驶5000 km后报废;若把它安装在后轮,则自行车行驶3000km后报废,行驶一定路程后可以交换前、后轮胎.如果交换前、后轮胎,要使一辆自行车的一对新轮胎同时报废,那么这辆车将能行驶___km.
【正确答案】3750
【详解】设每个新轮胎报废时的总磨损量为k,则安装在前轮的轮胎每行驶1km磨损量为,安装在后轮的轮胎每行驶1km的磨损量为.又设一对新轮胎交换位置前走了xkm,交换位置后走了ykm.分别以一个轮胎的总磨损量为等量关系列方程,有,两式相加,得,则x+y==3750(千米).
故答案为3750.
点睛:本题考查了二元方程组的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程组,再求解.利用二元方程组求解的应用题一般情况下题中要给出两个等量关系,准确的找到等量关系并用方程组表示出来是解题的关键.
13. 小明家洗手盆上装有一种抬启式水龙头(如图1),完全开启后,水流路线呈抛物线,把手端点A,出水口B和落水点C恰好在同一直线上,点A至出水管BD的距离为12cm,洗手盆及水龙头的相关数据如图2所示,现用高10.2cm的圆柱型水杯去接水,若水流所在抛物线点D和杯子上底面E,则点E到洗手盆内侧的距离EH为_____cm.
【正确答案】24﹣8.
【详解】试题解析:如图所示,建立直角坐标系,过A作AG⊥OC于G,交BD于Q,过M作MP⊥AG于P,由题可得,AQ=12,PQ=MD=6,故AP=6,AG=36,∴Rt△APM中,MP=8,故DQ=8=OG,∴BQ=12﹣8=4,由BQ∥CG可得,△ABQ∽△ACG,∴,即,∴CG=12,OC=12+8=20,∴C(20,0),又∵水流所在抛物线点D(0,24)和B(12,24),∴可设抛物线为,把C(20,0),B(12,24)代入抛物线,可得: ,解得:,∴抛物线为,又∵点E的纵坐标为10.2,∴令y=10.2,则,解得x1=,x2=(舍去),∴点E的横坐标为,又∵ON=30,∴EH=30﹣()=.故答案为.
点睛:本题以水龙头接水为载体,考查了二次函数的应用以及相似三角形的应用,在运用数学知识解决问题过程中,关注核心内容,经历测量、运算、建模等数学实践为主线的问题探究过程,突出考查数学的应用意识和解决问题的能力,蕴含数学建模,引导学生关注生活,利用数学方法解决实际问题.
14. 如图,铁路的路基是等腰梯形ABCD,斜坡AD、BC的坡度i=1:1.5,路基AE高为3米,现由单线改为复线,路基需加宽4米,(即AH=4米),加宽后也成等腰梯形,且GH、BF斜坡的坡度=1:2,若路长为10000米,则加宽的土石方量共是_____立方米.
【正确答案】1.65×105
【详解】过H点作HJ⊥GF于J,
∵i=1:1.5,AE=3,
∴DE=4.5,
∴DC=13.
∴S梯形ABCD=(4+13)×3÷2=25.5(米2).
又∵GH、BF斜坡的=1:2,
∴GJ为6,
∴GF=2GJ+8=20,S梯形BFGH=(8+20)×3÷2=42(米2).
∴加宽的土石方量=(42-25.5)×10000=165000=1.65×105立方米.
故1.65×105.
15. 同时掷两个质地均匀的六面体骰子,两个骰子向上一面点数相同的概率是____.
【正确答案】
【详解】列表得:
(1,6)
(2,6)
(3,6)
(4,6)
(5,6)
(6,6)
(1,5)
(2,5)
(3,5)
(4,5)
(5,5)
(6,5)
(1,4)
(2,4)
(3,4)
(4,4)
(5,4)
(6,4)
(1,3)
(2,3)
(3,3)
(4,3)
(5,3)
(6,3)
(1,2)
(2,2)
(3,2)
(4,2)
(5,2)
(6,2)
(1,1)
(2,1)
(3,1)
(4,1)
(5,1)
(6,1)
∴一共有36种情况,两个骰子点数相同为(1,1),(2,2),(3,3),(4,4),(5,5),(6,6),共6种可能.
∴两个骰子点数相同的概率是.
列表法可以没有重复没有遗漏的列出所有可能的结果,适合于两步完成的;
解题时还要注意是放回试验还是没有放回试验.用到的知识点为:概率=所求情况数与总情况数之比.
16. 在平面直角坐标系中,点A坐标为(1,0),线段OA绕原点O沿逆时针方向旋转45°,并且每次的长度增加一倍,例如:OA1=2OA,∠A1OA=45°.按照这种规律变换下去,点A2017的纵坐标为_____.
【正确答案】22016•
【详解】根据点A0的坐标为(1,0),可得OA=1.然后根据题意,将线段OA绕原点O沿逆时针方向旋转45°,可知360°÷45°=8,可得A1、A9、A17、···A2017都在象限, 再根据OA1=2OA=2,∠A1OA=45°,可求得A1的纵坐标为,
同理可得,A9放入纵坐标为;
∴A2017的纵坐标为.
故答案为.
三、解 答 题:本大题共9小题,共72分.
17. 计算下列各式:
(1) ;
(2) ;
(3)
(4) .
【正确答案】(1)(2)0(3)0(4)1
【详解】试题分析:(1)先根据异分母的分式的加减法,先把前两个分式通分,再求和,依次计算下去即可;
(2)先把分子添项,构成能分组分解因式的式子,把分母利用整式的乘法展开,然后把分母分子分解因式,利用同分母的分式相加减的逆运算约分化简即可;
(3)根据立方差和立方和公式进行分子分母的因式分解,然后再约分化简即可;
(4)设x﹣y=a,y﹣z=b,z﹣x=c,利用换元法进行约分化简即可.
试题解析:(1)
=++
=+
=;
(2)
=++
=++﹣﹣﹣
=0;
(3)
=+﹣
=+﹣
=0;
(4)设x﹣y=a,y﹣z=b,z﹣x=c,则
=﹣﹣﹣
=﹣
=
=1.
18. 解没有等式组:,并将解集在数轴上表示出来.
【正确答案】-7<≤1.数轴见解析.
【分析】分别求出各没有等式的解集,再求出其公共解集,并在数轴上表示出来即可.
【详解】解:
解没有等式①,得≤1,
解没有等式②,得>-7,
∴没有等式组的解集为-7<≤1.
在数轴上表示没有等式组的解集为
故答案为-7<≤1.
本题考查了解一元没有等式组,熟知“取大,小小取小,大小小大中间找,小小找没有了“的原则是解此题的关键.
19. 图(a)是正方形纸板制成的一副七巧板.
(1)请你在图(a)中给它的每一小块用①~⑦编号(编号直接标在每一小块对应图形内部的空白处;每小块只能与一个编号对应,每个编号只能和一个小块对应),并同时满足以下三个条件:
条件1:编号为①~③的三小块可以拼成一个轴对称图形;
条件2:编号为④~⑥的三小块可以拼成一个对称图形;
条件3:编号为⑦的小块是对称图形.
(2)请你在图(b)中画出编号为①~③的三小块拼出的轴对称图形;在图(c)中画出编号为④~⑥的三小块拼出的对称图形.(注意:没有编号没有得分)
【正确答案】答案见解析
【详解】试题分析:(1)根据七巧板的结构组成及条件1、2和3的叙述分别标上数字即可;
(2)根据轴对称图形的性质,拼凑出任一轴对称图形即可(答案没有);拼凑一个平行四边形即可.
试题解析:答案没有,如下图:(注意:没有编号没有得分)
点睛:此题主要考查了对称图形以及轴对称图形的拼凑方法,灵活应用对称图形以及轴对称图形性质是解决问题的关键.
20. 近几年,随着电子商务的发展,“电商包裹件”占“快递件”总量的比例逐年增长,根据企业财报,某网站得到如下统计表:
年份
2014
2015
2016
2017(预计)
快递件总量(亿件)
140
207
310
450
电商包裹件(亿件)
98
153
235
351
(1)请选择适当的统计图,描述2014﹣2017年“电商包裹件”占当年“快递件”总量的百分比(到1%);
(2)若2018年“快递件”总量将达到675亿件,请估计其中“电商包裹件”约为多少亿件?
【正确答案】(1)图形见解析(2)估计其中“电商包裹件”约为540亿件
【详解】试题分析:(1)分别计算各年的百分比,并画统计图,也可以画条形图;
(2)从2014到2017发现每年上涨两个百分点,所以估计2018年的百分比为80%,据此计算即可.
试题解析:(1)2014:98÷140=0.7,
2015:153÷207≈0.74,
2016:235÷310≈0.76,
2017:351÷450=0.78,
画统计图如下:
(2)根据统计图,可以预估2018年“电商包裹件”占当年“快递件”总量的80%,
所以,2018年“电商包裹件”估计约为:675×80%=540(亿件),
答:估计其中“电商包裹件”约为540亿件.
点睛:本题考查了统计图的选择、百分比的计算,明确折线统计图的特点:①能清楚地反映事物的变化情况.②显示数据变化趋势.
21. 如图,直线EF交⊙O于A、B两点,AC是⊙O直径,DE是⊙O的切线,且DE⊥EF,垂足为E.
(1)求证:AD平分∠CAE;
(2)若DE=4cm,AE=2cm,求⊙O的半径.
【正确答案】(1)证明见解析;(2)⊙O的半径是5.
【详解】图形的认识→角平分线及其性质; 圆→切线的性质和判定; 圆→圆及其有关概念;
22. 某学校要制作一批工作的宣传材料.甲公司提出:每份材料收费10元,另收1000元的版面设计费;乙公司提出:每份材料收费20元,没有收版面设计费.请你帮助该学校选择制作.
【正确答案】当制作材料为100份时,两家公司收费一样,选择哪家都可行;当制作材料超过100份时,选择甲公司比较合算;当制作材料少于100份时,选择乙公司比较合算.
【详解】试题分析:设制作x份材料时,甲公司收费y1元,乙公司收费y2元,分别表示出甲乙两公司的收费标准,然后通过y1=y2, y1>y2,y1<y2,分别求出x的值或范围,比较即可设计.
试题解析:设制作x份材料时,甲公司收费y1元,乙公司收费y2元,
则y1=10x+1000,y2=20x,
由y1=y2,得10x+1000=20x,解得x=100
由y1>y2,得10x+1000>20x,解得x<100
由y1<y2,得10x+1000<20x,解得x>100
所以,当制作材料为100份时,两家公司收费一样,选择哪家都可行;
当制作材料超过100份时,选择甲公司比较合算;
当制作材料少于100份时,选择乙公司比较合算.
23. 已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个没有相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象没有第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的整数值.
【正确答案】(1)证明见解析;(2)k≤1;(3)2.
【详解】试题分析:(1)求出方程的判别式△的值,利用配方法得出△>0,根据判别式的意义即可证明;
(2)由于二次函数的图象没有第三象限,又△=(k﹣5)2﹣4(1﹣k)=(k﹣3)2+12>0,所以抛物线的顶点在x轴的下方一、二、四象限,根据二次项系数知道抛物线开口向上,由此可以得出关于k的没有等式组,解没有等式组即可求解;
(3)设方程的两个根分别是x1,x2,根据题意得(x1﹣3)(x2﹣3)<0,根据一元二次方程根与系数的关系求得k的取值范围,再进一步求出k的整数值.
试题解析:(1)证明:∵△=(k﹣5)2﹣4(1﹣k)=k2﹣6k+21=(k﹣3)2+12>0,∴无论k为何值,方程总有两个没有相等实数根;
(2)解:∵二次函数的图象没有第三象限,∵二次项系数a=1,∴抛物线开口方向向上,∵△=(k﹣3)2+12>0,∴抛物线与x轴有两个交点,设抛物线与x轴的交点的横坐标分别为x1,x2,∴x1+x2=5﹣k>0,x1x2=1﹣k≥0,解得k≤1,即k的取值范围是k≤1;
(3)解:设方程的两个根分别是x1,x2,根据题意,得(x1﹣3)(x2﹣3)<0,即x1x2﹣3(x1+x2)+9<0,又x1+x2=5﹣k,x1x2=1﹣k,代入得,1﹣k﹣3(5﹣k)+9<0,解得k<.则k的整数值为2.
24. 如图1,在矩形ABCD中,AB=6cm,BC=8cm,E、F分别是AB、BD的中点,连接EF,点P从点E出发,沿EF方向匀速运动,速度为1cm/s,同时,点Q从点D出发,沿DB方向匀速运动,速度为2cm/s,当点P停止运动时,点Q也停止运动.连接PQ,设运动时间为t(0<t<4)s,解答下列问题:
(1)求证:△BEF∽△DCB;
(2)当点Q在线段DF上运动时,若△PQF的面积为0.6cm2,求t的值;
(3)如图2过点Q作QG⊥AB,垂足为G,当t为何值时,四边形EPQG为矩形,请说明理由;
(4)当t为何值时,△PQF为等腰三角形?试说明理由.
【正确答案】(1)证明见解析(2)2;(3);(4)t=1或3或或秒时,△PQF是等腰三角形
【详解】解:(1)∵四边形是矩形,
在中,
分别是的中点,
(2)如图1,过点作于,
(舍)或秒;
四边形为矩形时,如图所示:
解得:
当点在上时,如图2,
当点在上时, 如图3,
时,如图4,
时,如图5,
综上所述,或或或秒时,是等腰三角形.
25. 建立模型:如图1,已知△ABC,AC=BC,∠C=90°,顶点C在直线l上.
实践操作:过点A作AD⊥l于点D,过点B作BE⊥l于点E,求证:△CAD≌△BCE.
模型应用:(1)如图2,在直角坐标系中,直线l1:y=x+4与y轴交于点A,与x轴交于点B,将直线l1绕着点A顺时针旋转45°得到l2.求l2函数表达式.
(2)如图3,在直角坐标系中,点B(8,6),作BA⊥y轴于点A,作BC⊥x轴于点C,P是线段BC上的一个动点,点Q(a,2a﹣6)位于象限内.问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形,若能,请求出此时a的值,若没有能,请说明理由.
【正确答案】实践操作:详见解析;模型应用:(1)y=x+4;(2)A、P、Q可以构成以点Q为直角顶点的等腰直角三角形,a的值为或4.
【分析】操作:根据余角的性质,可得∠ACD=∠CBE,根据全等三角形的判定,可得答案;
应用(1)根据自变量与函数值的对应关系,可得A、B点坐标,根据全等三角形的判定与性质,可得CD,BD的长,根据待定系数法,可得AC的解析式;
(2)分两种情况讨论:①当Q在直线AP的下方时,②当Q在直线AP的上方时.根据全等三角形的性质,可得关于a的方程,根据解方程,可得答案.
【详解】操作:如图1:
∵∠ACD+∠BCE=90°,∠BCE+∠CBE=90°,∴∠ACD=∠CBE.
在△ACD和△CBE中,∵,∴△CAD≌△BCE(AAS);
(1)∵直线yx+4与y轴交于点A,与x轴交于点B,∴A(0,4)、B(﹣3,0).如图2:
过点B做BC⊥AB交直线l2于点C,过点C作CD⊥x轴.
在△BDC和△AOB中,∵,∴△BDC≌△AOB(AAS),∴CD=BO=3,BD=AO=4.OD=OB+BD=3+4=7,∴C点坐标为(﹣7,3).
设l2的解析式为y=kx+b,将A,C点坐标代入,得:,解得:,l2的函数表达式为yx+4;
(2)由题意可知,点Q是直线y=2x﹣6上一点.分两种情况讨论:
①当Q在直线AP的下方时,如图3,过点Q作EF⊥y轴,分别交y轴和直线BC于点E、F.
在△AQE和△QPF中,∵,∴△AQE≌△QPF(AAS),AE=QF,即6﹣(2a﹣6)=8﹣a,解得:a=4.
②当Q在直线AP的上方时,如图4,过点Q作EF⊥y轴,分别交y轴和直线BC于点E、F,AE=2a﹣12,FQ=8﹣a.
在△AQE和△QPF中,∵,∴△AQE≌△QPF(AAS),AE=QF,即2a﹣12=8﹣a,解得:a.
综上所述:A.P、Q可以构成以点Q为直角顶点的等腰直角三角形,a的值为或4.
本题考查了函数综合题,利用余角的性质得出∠ACD=∠CBE是解题的关键,又利用了全等三角形的判定;利用了全等三角形的性质得出CD,BD的长是解题的关键,又利用了待定系数法求函数解析式;利用全等三角形的性质得出关于a的方程是解题的关键,要分类讨论,以防遗漏.
2022-2023学年福建省福州市中考数学专项突破仿真模拟卷
(二模)
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
1.在四个数﹣3,0,,﹣1中,最小的是( )中考
A.﹣3 B.0 C. D.﹣1
A.2.如图,该几何体的主视图是
中考
A. B. C. D.
3.如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是( )
中考
A.从点P向北偏西45°走3km到达l B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45° D.从点P向北走3km后,再向西走3km到达l
4.下列运算正确的是 中考
A. B. C. D.中考
5.学校组织“热爱祖国”演讲比赛,小娜演讲内容得90分,语言表达得88分,若按演讲内容占60%、语言表达占40%的比例计算总成绩,则小娜的总成绩是( )
A.90分 B.88分 C.89分 D.89.2分中考
6.我国古代数学著作《九章算术》中有这样一个问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意即:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处.折断处离地面的高度是 (注:其中的丈、尺是长度单位,1丈尺)
A.3尺 B.4尺 C.4.55尺 D.5尺
7.将等边三角形、正方形、正五边形按如图所示的方式摆放,如果∠1=41°,∠2=51°,那么∠3等于( )
中考
A.5° B.10° C.15° D.20°
8.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中如图所示,则关于x的不等式k1x+b>k2x的解为( )
中考
A.x<﹣1 B.x>﹣1 C.x>2 D.x<2中考
9.如图,PA是⊙O的切线,OP交⊙O于点B,如果,OB=1,那么BP的长是( )中考
A.4 B.2 C.1 D.
10.设A(﹣2,y1),B(﹣1,y2),C(2+,y3)是抛物线y=﹣ax2+2ax﹣1上的三点,则y1,y2,y3的大小关系可能为( )
A.y2>y1>y3 B.y2>y3>y1 C.y3>y2>y1 D.y3>y1>y2
二、填空题:本题共6小题,每小题4分,共24分。
11.计算:(π﹣1)0+|﹣3|﹣= .中考
12.某市某天的最高气温为﹣3℃,最低气温为﹣5℃,这天的温差是 .中考
13.如图是某校举办数学竞赛参赛同学的决赛成绩,则该决赛成绩的中位数为 分.中考
中考
14.已知扇形的弧长为2πcm,半径为4cm,则此扇形的面积为 cm2.
15.如图,正方形ABCD的边长为4,E为AB边上一点,tan∠ADE=,M为ED的中点,过点M作DE的垂线,交边AD于点P,若点N在射线PM上,且由点E、M、N组成的三角形与△AED相似,则PN的长为 .
中考
16.如图,点A在x轴正半轴上,B(5,4),四边形AOCB为平行四边形,反比例函数y=的图象经过点C,交AB边于点D,则点D的坐标为 .中考
三、解答题:本题共9小题,共86分。解答应写出文字说明、证明过程或演算步骤。中考
17.解不等式组:.
18.先化简,再求值:,其中a满足a2﹣2a﹣1=0.中考
中考
中考
19.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.如图.
(1)∠BEC= °;(2)在图中已有的三角形中,找到一对全等的三角形,并证明你的结论;
中考
中考
20.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6中考
(1)尺规作图:作AB边上的中点D和△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.
21.某商场购进A、B两种商品共200件进行,其中A商品的件数不大于B商品的件数,且不小于50件,A、B两种商品的进价、售价如表:中考
A中考
B
进价(元/件)
150
130
售价(元/件)中考
220
195
(1)设商场购进A商品的件数为x(件),购进A、B两种商品全部售出后获得的利润为y(元),求y与x之间的函数关系式,并写出x的取值范围;(2)在(1)条件下,商场决定在活动中每售出一件A商品,就从一件A商品的利润中捐给慈善基金m(5<m≤10)元,求该商场售完所有商品并捐献慈善资金后获得的最大利润.
22.菱形ABCD的边长为6,∠D=60°,点E在边AD上运动.(1)如图1,当点E为AD的中点时,求AO:CO的值;(2)如图2,F是AB上的动点,且满足BF+DE=6,求证:△CEF是等边三角形.中考
中考
中考
23.某生活超市有一专柜预代理甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从数据中随机各抽取50天,统计每日的数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润为:甲公司给超市每天基本费用为90元,另外每一件提成1元;乙公司给超市每天的基本费用为130元,每日数量不超过83件没有提成,超过83件的部分每件提成10元.(1)求乙公司给超市的日利润y(单位:元)与日数量n的函数关系;(2)若将频率视为概率,回答下列问题:①求甲公司产品数量不超过87件的概率;②如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行?并说明理由.中考
中考
24.如图,在平面直角坐标系中,点A、C分别在x轴正半轴、y轴正半轴上,四边形OABC为矩形,AB=4,cos∠ACB=,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.(1)求证:△AEF∽△DCE;(2)当△CEF是等腰三角形时,求DE的长;(3)当CF的长最小时,求△CED的内切圆圆心G的坐标.
25.如图,抛物线y=x2+bx+c与x轴交于A、B两点,且A(﹣1,0),对称轴为直线x=2.中考
(1)求该抛物线的函数表达式;(2)直线l过点A且在第一象限与抛物线交于点C.当∠CAB=45°时,求点C的坐标;(3)点D在抛物线上与点C关于对称轴对称,点P是抛物线上一动点,令P(xP,yP),当1≤xP≤a,1≤a≤5时,求△PCD面积的最大值(可含a表示).中考
答案与解析
一、选择题:本题共10小题,每小题4分,共40分。在每小题给出的四个选项中,只有一项是符合要求的。
1.在四个数﹣3,0,,﹣1中,最小的是( )中考
A.﹣3 B.0 C. D.﹣1
解:∵|﹣3|=3,|﹣1|=1,3>1,∴﹣3<﹣1,
∴﹣3<﹣1<0<,∴在﹣3,0,,﹣1这四个数中,最小的是﹣3.答案:A.
2.如图,该几何体的主视图是 中考
中考
A. B. C. D.中考
解:从正面看,底层是一个矩形,上层的右边是一个矩形.故选:.
3.如图,从笔直的公路l旁一点P出发,向西走6km到达l;从P出发向北走6km也到达l.下列说法错误的是( )
A.从点P向北偏西45°走3km到达l B.公路l的走向是南偏西45°
C.公路l的走向是北偏东45° D.从点P向北走3km后,再向西走3km到达l
解:如图,由题意可得△PAB是腰长6km的等腰直角三角形,则AB=6km,
如图所示,过P点作AB的垂线PC,则PC=3km,
则从点P向北偏西45°走3km到达l,选项A错误;
则公路l的走向是南偏西45°或北偏东45°,选项B,C正确;中考
则从点P向北走3km后到达BP中点D,此时CD为△PAB的中位线,故CD=AP=3,故再向西走3km到达l,选项D正确.答案:A.
中考
4.下列运算正确的是
A. B. C. D.
解:选项,故选项错误,选项,故选项错误,
选项,故选项错误,选项,故选项正确,故选:.
5.学校组织“热爱祖国”演讲比赛,小娜演讲内容得90分,语言表达得88分,若按演讲内容占60%、语言表达占40%的比例计算总成绩,则小娜的总成绩是( )中考
A.90分 B.88分 C.89分 D.89.2分中考
解:=89.2(分),答案:D.
6.我国古代数学著作《九章算术》中有这样一个问题:“今有竹高一丈,末折抵地,去本三尺,问折者高几何?”意即:一根竹子高1丈,折断后竹子顶端落在离竹子底端3尺处.折断处离地面的高度是 (注:其中的丈、尺是长度单位,1丈尺)
中考
A.3尺 B.4尺 C.4.55尺 D.5尺中考
解:设竹子折断处离地面尺,则斜边为尺,
根据勾股定理得:.解得:,
答:折断处离地面的高度为4.55尺.故选:.
7.将等边三角形、正方形、正五边形按如图所示的方式摆放,如果∠1=41°,∠2=51°,那么∠3等于( )
A.5° B.10° C.15° D.20°
解:等边三角形的内角的度数是60°,正方形的内角度数是90°,正五边形的内角的度数是:(5﹣2)×180°=108°,则∠3=360°﹣60°﹣90°﹣108°﹣∠1﹣∠2=10°.答案:B.中考
8.直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中如图所示,则关于x的不等式k1x+b>k2x的解为( )
A.x<﹣1 B.x>﹣1 C.x>2 D.x<2
解:从图象可知:两直线的图象交点坐标是(﹣1,2),
∴关于x的不等式k1x+b>k2x的解集为x>﹣1,答案:B.
9.如图,PA是⊙O的切线,OP交⊙O于点B,如果,OB=1,那么BP的长是( )
中考
A.4 B.2 C.1 D.
解:连接OA,∵PA为⊙O的切线,∴∠OAP=90°,
∵sinP=,OB=1,∴AO=1,则OP=2,故BP=2﹣1=1.答案:C.
中考
10.设A(﹣2,y1),B(﹣1,y2),C(2+,y3)是抛物线y=﹣ax2+2ax﹣1上的三点,则y1,y2,y3的大小关系可能为( )
A.y2>y1>y3 B.y2>y3>y1 C.y3>y2>y1 D.y3>y1>y2中考
解:∵抛物线y=﹣ax2+2ax﹣1,∴抛物线的对称轴是直线x=﹣=1,
∵A(﹣2,y1),B(﹣1,y2),C(2+,y3)是抛物线y=﹣ax2+2ax﹣1上的三点,
∴点C关于对称轴x=1的对称点是(﹣,y3),
∵﹣2<﹣<﹣1,若﹣a>0时,则y2>y3>y1,若﹣a<0时,则y1>y3>y2,答案:B中考
二、填空题:本题共6小题,每小题4分,共24分。
11.计算:(π﹣1)0+|﹣3|﹣= .
解:原式=1+3﹣2=4﹣2,答案:4﹣2.
12.某市某天的最高气温为﹣3℃,最低气温为﹣5℃,这天的温差是 .中考
解:(﹣3)﹣(﹣5)=﹣3+5=2(℃).答案:2℃.
13.如图是某校举办数学竞赛参赛同学的决赛成绩,则该决赛成绩的中位数为 分.
解:2+7+5+3=17(人),17个参赛学生成绩的中位数为第9个,
∴所有参赛学生成绩的中位数落在98分这个组内,中位数是98分,答案:98.中考
14.已知扇形的弧长为2πcm,半径为4cm,则此扇形的面积为 cm2.
解:∵扇形的弧长为2πcm,半径为4cm,∴该扇形的面积为×2π×4=4π(cm2),答案:4π.
15.如图,正方形ABCD的边长为4,E为AB边上一点,tan∠ADE=,M为ED的中点,过点M作DE的垂线,交边AD于点P,若点N在射线PM上,且由点E、M、N组成的三角形与△AED相似,则PN的长为 .
中考
解:∵正方形ABCD的边长为4,tan∠ADE=,∴DE==5,中考
∵M为ED的中点,∴DM=EM=,在Rt△PMD中,PM=DM•tan∠ADE=×=,
如图:中考
①若点N在线段PM上,△EMN1∽△DAE时,
∴,即,解得:MN1=,∴PN1=PM﹣MN1=0;中考
②若点N在线段PM延长线上,△EMN2∽△DAE时,
∴,即,解得:MN2=,∴PN2=PM+MN2=;
③若点N在线段PM延长线上,△EMN3∽△EAD时,中考
∴,即,解得:MN3=,∴PN3=PM+MN3=.
答案:0或或.
16.如图,点A在x轴正半轴上,B(5,4),四边形AOCB为平行四边形,反比例函数y=的图象经过点C,交AB边于点D,则点D的坐标为 .中考
解:作CE⊥OA于E,
∵B(5,4),四边形AOCB为平行四边形,∴C的纵坐标为4,
∵反比例函数y=的图象经过点C,∴4=,∴x=2,
∴C(2,4),OA=BC=5﹣2=3,∴A(3,0),设直线OC为y=kx,中考
把C(2,4)代入得,4=2k,解得k=2,∵AB∥OC,中考
∴设直线AB的解析式为y=2x+b,代入A(3,0)解得,b=﹣6,∴直线AB的解析式为y=2x﹣6,中考
由得或,∴点D的坐标为(4,2),答案:(4,2).中考
三、解答题:本题共9小题,共86分。解答应写出文字说明、证明过程或演算步骤。
17.解不等式组:.
解:,由①得:x≥﹣5,由②得:x<3,
∴不等式组的解集是﹣5≤x<3.中考
18.先化简,再求值:,其中a满足a2﹣2a﹣1=0.
解:=÷=•
=•=﹣=﹣,
∵a2﹣2a﹣1=0,∴a2﹣2a=1,当a2﹣2a=1时,原式=﹣=﹣1.
19.在矩形ABCD中,BE平分∠ABC交CD边于点E.点F在BC边上,且FE⊥AE.如图.
(1)∠BEC= °;(2)在图中已有的三角形中,找到一对全等的三角形,并证明你的结论;中考
解:(1)∵四边形ABCD为矩形,∴∠ABC=∠BCD=90°,
∵BE平分∠ABC,∴∠EBC=45°,∴∠BEC=45°,答案:45;
(2)△ADE≌△ECF,理由如下:
∵四边形ABCD是矩形,∴∠ABC=∠C=∠D=90°,AD=BC.
∵FE⊥AE,∴∠AEF=90°.∴∠AED+∠FEC=180°﹣∠AEF=90°.
∵∠AED+∠DAE=90°,∴∠FEC=∠EAD,
∵BE平分∠ABC,∴∠EBC=∠ABC=45°.中考
∴∠BEC=45°.∴∠EBC=∠BEC.∴BC=EC.∴AD=EC.
在△ADE和△ECF中,,∴△ADE≌△ECF(ASA).
20.如图,在△ABC中,点D是AB边上的中点,已知AC=4,BC=6
(1)尺规作图:作AB边上的中点D和△BCD关于点D的中心对称图形;
(2)根据图形说明线段CD长的取值范围.中考
中考
解:(1)中点D如图所示,△ADE即为所求.
(2)由题意AE=BC=6,∴6﹣4<EC<4+6,∴2<EC<10,
∵EC=2CD,∴1<CD<5.中考
21.某商场购进A、B两种商品共200件进行,其中A商品的件数不大于B商品的件数,且不小于50件,A、B两种商品的进价、售价如表:
A中考
B中考
进价(元/件)
150
130
售价(元/件)中考
220中考
195
(1)设商场购进A商品的件数为x(件),购进A、B两种商品全部售出后获得的利润为y(元),求y与x之间的函数关系式,并写出x的取值范围;(2)在(1)条件下,商场决定在活动中每售出一件A商品,就从一件A商品的利润中捐给慈善基金m(5<m≤10)元,求该商场售完所有商品并捐献慈善资金后获得的最大利润.
解:(1)由题意可得,y=(220﹣150)x+(195﹣130)(200﹣x)=5x+13000,中考
∵A商品的件数不大于B商品的件数,且不小于50件,
∴50≤x≤200﹣x,解得50≤x≤100,
即y与x之间的函数关系式是y=5x+13000(50≤x≤100);
(2)设最后获得的利润为w元,
由题意可得:w=y﹣mx=(5x+13000)﹣mx=(5﹣m)x+13000,中考
∵5<m≤10,∴5﹣m<0,∴w随x的增大而减小,中考
∵50≤x≤100,∴当x=50时,w取得最大值,此时w=13250﹣50m,中考
答:该商场售完所有商品并捐献慈善资金后获得的最大利润是(13250﹣50m)元.
22.菱形ABCD的边长为6,∠D=60°,点E在边AD上运动.(1)如图1,当点E为AD的中点时,求AO:CO的值;(2)如图2,F是AB上的动点,且满足BF+DE=6,求证:△CEF是等边三角形.
中考
(1)解:∵四边形ABCD是菱形,∴BC=AD=6,AD∥BC,中考
∵点E为AD的中点,∴AE=AD=3,
∵AD∥BC,∴△AOE∽△COB,∴===;中考
(2)证明:∵四边形ABCD是菱形,∴AB=BC,AD∥BC,∠B=∠D=60°,中考
∴∠CAE=∠ACB,△ABC是等边三角形,∴AC=BC,∠ACB=60°,∴∠EAC=60°=∠B,
∵AE+DE=AD=6,BF+DE=6,∴AE=BF,
在△ACE和△BCF中,,∴△ACE≌△BCF(SAS),
∴CE=CF,∠ACE=∠BCF,∴∠ACE+∠ACF=∠BCF+∠ACF=∠ACB=60°,中考
即∠ECF=60°,∴△CEF是等边三角形.
23.某生活超市有一专柜预代理甲乙两家公司的一种可相互替代的日常生活用品.经过一段时间分别单独试销甲乙两家公司的商品,从数据中随机各抽取50天,统计每日的数量,得到如下的频数分布条形图.甲乙两家公司给该超市的日利润为:甲公司给超市每天基本费用为90元,另外每一件提成1元;乙公司给超市每天的基本费用为130元,每日数量不超过83件没有提成,超过83件的部分每件提成10元.(1)求乙公司给超市的日利润y(单位:元)与日数量n的函数关系;(2)若将频率视为概率,回答下列问题:①求甲公司产品数量不超过87件的概率;②如果仅从日均利润的角度考虑,请你利用所学过的统计学知识为超市作出抉择,选择哪家公司的产品进行?并说明理由.
中考
解:(1)由题意得到,当0≤n≤83时,y=130元,当n>83时,y=130+(n﹣83)×10=10n﹣700,
∴乙公司给超市的日利润y(单位:元)与日数量n的函数关系为:y=;
(2)①甲公司产品数量不超过87件的概率为:=;
②设甲公司的给超市的日利润为x元,则x的所有可能的值为:171,174,177,180,183,
=(171×5+174×10+177×5+180×20+183×10)=178.2(元),中考
设乙公司的给超市的日利润为y元,则y的所有可能的值为:130,140,170,200,230,
=×(130×50+0×5+10×5+40×10+70×15+100×15)=190(元),中考
∵<,∴超市应代理乙公司的产品较为合适.
24.如图,在平面直角坐标系中,点A、C分别在x轴正半轴、y轴正半轴上,四边形OABC为矩形,AB=4,cos∠ACB=,点D与点A关于y轴对称,点E、F分别是线段AD、AC上的动点(点E不与点A、D重合),且∠CEF=∠ACB.(1)求证:△AEF∽△DCE;(2)当△CEF是等腰三角形时,求DE的长;(3)当CF的长最小时,求△CED的内切圆圆心G的坐标.
中考
(1)证明:如图,∵四边形OABC为矩形,∴OA∥BC,∴∠ACB=∠CAD,中考
∵点D与点A关于y轴对称,∴AC=CD,∴∠CDA=∠CAD=∠ACB,
∵∠CEF=∠ACB,∴∠CEF=∠CDA,∴∠CED+∠AEF=∠CED+∠DCE,
∴∠AEF=∠DCE,∴△AEF∽△DCE;
(2)解:∵点E与点D不重合,∴点F与点A不重合,
∴∠CFE>∠CAD,∴∠CFE>∠CEF,∴CE≠CF,
①若CE=EF,∵△AEF∽△DCE,∴△AEF≌△DCE,∴CD=AE,中考
∵cos∠ACB=,设BC=3k,则AC=5k,由勾股定理得AB=4k,
∵AB=4,∴k=1,∴BC=3,AC=5,
∴OA=OD=3,AD=6,CD=5,∴AE=5,∴DE=1;中考
②若CF=EF,则∠ECF=∠CEF=∠CDA=∠CAD,∴△CEF∽△DAC,∴==,中考
∵△AEF∽△DCE,∴=,∴=,∴=,∴DE=,
综上,DE的长为1或;中考
(3)解:设DE=x,CD=y,∵△AEF∽△DCE,∴=,∴=,
∴y=x2﹣x+5(0<x<6),∴y=(x﹣3)2+,∴当x=3时,y有最小值,中考
即当DE的长为3时,CF长最小,最小值为,此时,点E与点O重合,
设⊙G切△DCE三边于M、N、P,如图,连接GM,GN,中考
设EN=EM=半径r,则CP=CN=4﹣r,DP=DM=3﹣r,中考
∵CP+DP=CD,∴4﹣r+3﹣r=5,∴r=1,∴点G的坐标是(﹣1,1).中考
25.如图,抛物线y=x2+bx+c与x轴交于A、B两点,且A(﹣1,0),对称轴为直线x=2.
(1)求该抛物线的函数表达式;(2)直线l过点A且在第一象限与抛物线交于点C.当∠CAB=45°时,求点C的坐标;(3)点D在抛物线上与点C关于对称轴对称,点P是抛物线上一动点,令P(xP,yP),当1≤xP≤a,1≤a≤5时,求△PCD面积的最大值(可含a表示).
解:(1)抛物线过A(﹣1,0),对称轴为x=2,
∴,解得,∴抛物线表达式为y=x2﹣4x﹣5;
(2)过点C作CE⊥x轴于点E,
中考
∵∠CAB=45°,∴AE=CE,
设点C的横坐标为xc,则纵坐标为yc=xc+1,∴C(xc,xc+1),
代入y=x2﹣4x﹣5得,xc+1=﹣4xc﹣5,解得xc=﹣1(舍去),xc=6,∴yc=7,
∴点C的坐标是(6,7);中考
(3)由(2)得C的坐标是(6,7),中考
∵对称轴x=2,∴点D的坐标是(﹣2,7),∴CD=8,
∵CD与x轴平行,点P在x轴下方,设△PCD以CD为底边的高为h,则h=|yp|+7,
∴当|yp|取最大值时,△PCD的面积最大,∵1≤xp≤a,1≤a≤5,
①当1≤a<2时,1≤xp≤a,此时y=x2﹣4x﹣5在1≤xp≤a上y随x的增大而减小,
∴|yp|max=|a2﹣4a﹣5|=5+4a﹣a2,∴h=|yp|+7=12+4a﹣a2,∴△PCD的最大面积为:
Smax=×CD×h=×8×(12+4a﹣a2)=48+16a﹣4a2;
②当2≤a≤5时,此时y=x2﹣4x﹣5的对称轴x=2含于1≤xp<a内,
∴|yp|max=|22﹣4×2﹣5|=9,∴h=9+7=16,中考
∴△PCD的最大面积为Smax=×CD×h=×8×16=64,中考
综上所述:当1≤a<2时,△PCD的最大面积为48+16a﹣4a2;
当2≤a≤5时,△PCD的最大面积为64
2022-2023学年福建省泉州市中考数学专项突破仿真模拟卷(一模二模)含答案: 这是一份2022-2023学年福建省泉州市中考数学专项突破仿真模拟卷(一模二模)含答案,共54页。
2022-2023学年福建省福州市中考数学专项突破仿真模拟卷(一模二模)含答案: 这是一份2022-2023学年福建省福州市中考数学专项突破仿真模拟卷(一模二模)含答案,共48页。
2022-2023学年福建省龙岩市中考数学专项突破仿真模拟试题(一模二模)含解析: 这是一份2022-2023学年福建省龙岩市中考数学专项突破仿真模拟试题(一模二模)含解析,共59页。试卷主要包含了选一选,填 空 题,解 答 题等内容,欢迎下载使用。












