初中数学人教版七年级下册5.1.1 相交线获奖ppt课件

这是一份初中数学人教版七年级下册5.1.1 相交线获奖ppt课件，共19页。PPT课件主要包含了邻补角，对顶角，对顶角的性质，对顶角相等，能不能说一说理由呢，②有公共顶点，③没有公共边，①两条直线相交而成，③有一条公共边，邻补角互补等内容，欢迎下载使用。
1.理解邻补角与对顶角的概念；2.掌握邻补角与对顶角的性质，并能运用它们的性质进行角的计算及解决简单实际问题.
观察下列图片，你能从中找出2条直线吗？
活动 握紧把手时，随着两个把手之间的角逐渐变小，剪刀刃之间的角也相应变小直到剪开布片. 如果把剪刀的构造看作两条相交的直线，这就关系到两条相交直线所成的角的问题.
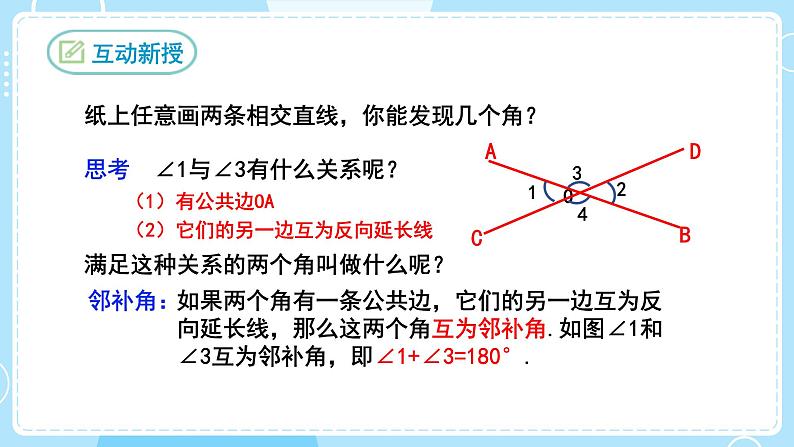
纸上任意画两条相交直线，你能发现几个角？
思考 ∠1与∠3有什么关系呢？
（1）有公共边OA（2）它们的另一边互为反向延长线
满足这种关系的两个角叫做什么呢？
如果两个角有一条公共边，它们的另一边互为反向延长线，那么这两个角互为邻补角.如图∠1和∠3互为邻补角，即∠1+∠3=180°.
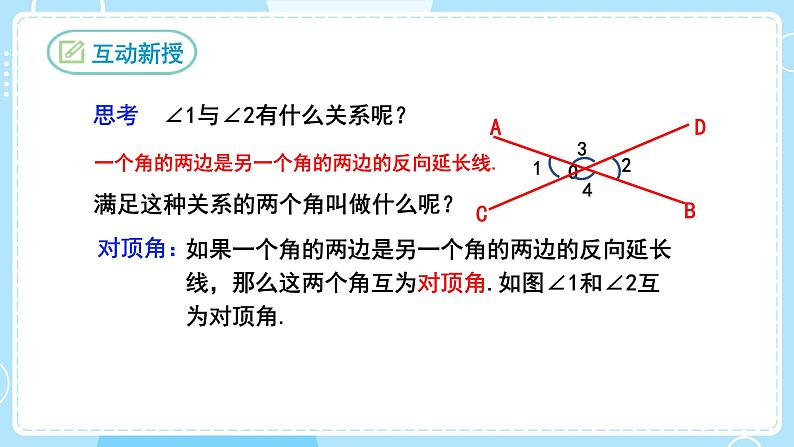
思考 ∠1与∠2有什么关系呢？
一个角的两边是另一个角的两边的反向延长线.
如果一个角的两边是另一个角的两边的反向延长线，那么这两个角互为对顶角.如图∠1和∠2互为对顶角.
思考 ∠1与∠2有什么数量关系呢？
∵∠1+∠3=180°，∠2+∠3=180°（邻补角的定义），∴∠1=∠2（同角的补角相等）.
解：由邻补角的定义，得 ∠2=180°-∠1=180°- 40°=140°； 由对顶角相等，得 ∠3 =∠1 =40° ∠4 =∠2 =140°.
例1 如图,直线a,b相交,∠1=40°,求 ∠2,∠3,∠4的度数.
1.下列各图中， ∠1 ，∠2是对顶角吗？
2.下列各图中， ∠1 ，∠2是邻补角吗？
1.判断 （1）有公共顶点且相等的两个角是对顶角.（ ） （2）两条直线相交，有两组对顶角. （ ） （3）两条直线相交所构成的四个角中有一个角是直角，那么其余的三个角也是直角. （ ）
2.如图，已知直线 AB，CD 相交于点 O，OE 平分∠COB，若∠EOB =55°，∠BOD的度数是 ．
3.如图,直线AB,CD相交于点O,∠EOC=70°,OA平分∠EOC，求∠BOD的度数.
解：∵OA平分∠EOC, ∴∠AOC= ∠EOC=35°, ∴∠BOD=∠AOC=35°.
1.两条直线a、b相交，其中2∠3=3∠1，求∠2的度数.
解：根据题意，∠1与∠3是邻补角， ∴∠1+∠3=180°， ∵2∠3=3∠1， ∴∠3=108°，∠1=72° 根据对顶角性质，得 ∠2=∠3=108°.
①两条直线相交形成的角；
①都是两条直线相交而成的角；
②两直线相交时，对顶角只有两对,邻补角有四对.
1.如图，直线AB、CD，EF相交于点O，∠1＝40°，∠BOC＝110°，求∠2的度数.
解：∵∠1=40°，∠BOC=110°(已知)， ∴∠BOF=∠BOC－∠1=110°－40°=70°. ∵∠BOF=∠2(对顶角相等)， ∴∠2=70°(等量代换)．
2.直线AB、CD交于点O，OE是∠AOD的平分线，已知∠AOC=50°.求∠DOE的度数.