【最新教材插图】4 整理和复习（课件PPT）

这是一份【最新教材插图】4 整理和复习（课件PPT），共19页。

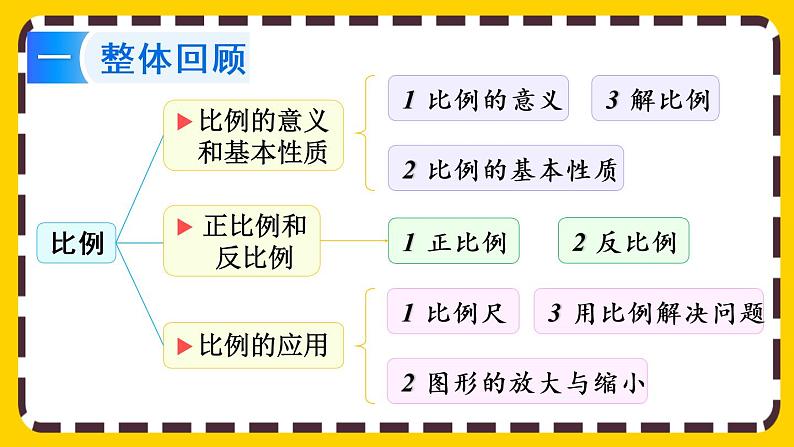
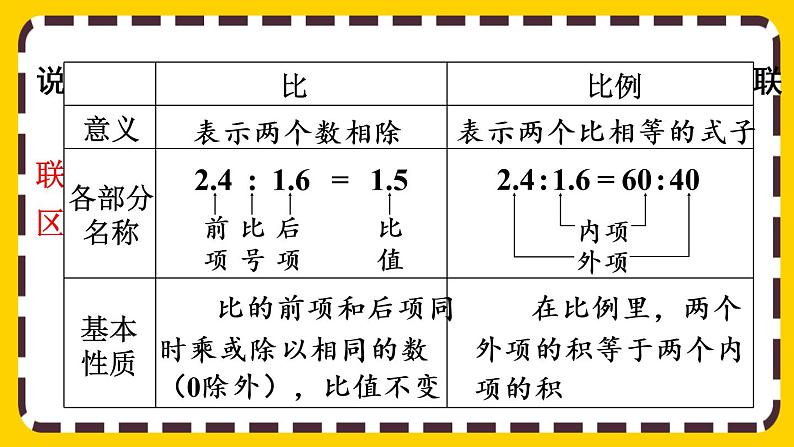
4 比例整理和复习人教版数学六年级下册表示两个比相等的式子叫做比例。1. 比例的意义： 在比例里，两个外项的积等于两个内项的积，这叫做比例的基本性质。2. 比例的基本性质：联系：比例是由两个比值相等的比组成的。区别：说一说：什么是比？什么是比例？比和比例有什么联 系和区别？ 如果已知比例中的任何三项，就可以求出这个比例中的另外一个未知项。求比例中的未知项的过程叫做解比例。3. 解比例：解比例的依据是什么？解下面的比例。 5x=4×6     解比例的依据是什么？解下面的比例。 1.2x=2.5×3  6.5:x=3.25:43.25x=6.5×4 x=81. 正比例： 两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的比值一定，这两种量就叫做成正比例的量，它们的关系叫做正比例关系。 2. 反比例： 两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的乘积一定，那么这两种量就叫做成反比例的量，它们的关系就叫做反比例关系。用字母表示为：xy =k（一定）1. 比例尺： 一幅图的图上距离和实际距离的比, 叫做这幅图的比例尺。2. 图形的放大与缩小： 要把一个图形按一定的比放大（缩小），只要把图形的各边按一定的比放大（缩小）即可。 图形按一定的比放大或缩小后，只是大小发生了变化，形状不变。3. 用比例解决问题： 用正比例关系列方程解题时，通常等号的两边写成分数比的形式。（若同一题中有两个未知量通常要用不同的字母表示。 ）1. 下面每个表中的两个量，哪些成比例关系？成正比 例关系还是反比例关系？哪些不成比例关系？ （1）从甲地到乙地的路程是240km，汽车行驶的速 度与时间如下表。速度/（千米/时）时间/时406504.86048031002.4 行驶速度×行驶时间=路程（一定），所以行驶速度和行驶时间成反比例关系。（教科书第63页）底面积/cm2体积/cm3550880101001616020200（2）圆锥的高是30cm，它的体积与底面积如下表。 所以体积与底面积成正比例关系。半径/cm面积/cm21π24π39π416π525π（3）圆的半径与面积如下表。 圆的面积与圆的半径的比值不一定，乘积也不一定，所以圆的面积与圆的半径不成比例关系。2.（1）李叔叔开车从甲地到乙地，前2小时行驶了 100km。照这样的速度，从甲地到乙地 一共要用3小时，甲乙两地相距多远？解：设甲乙两地相距 x km。答：甲乙两地相距150km。 2x=3×100 x=1502.（2）李叔叔开车从甲地到乙地一共用了3小时，每 小时行50km。原路返回每小时行60km，返 回时用了多长时间？解：设返回时用了x小时。60x=3×50答：返回时用了2.5小时。x=2.5 1.从课后习题中选取；2.完成本课时的习题。谢谢观看