人教版数学八下第19章单元同步测试提升卷B卷 原卷+解析

人教版数学 八下 第19章 单元同步测试提升卷B卷

一．选择题（共30分）

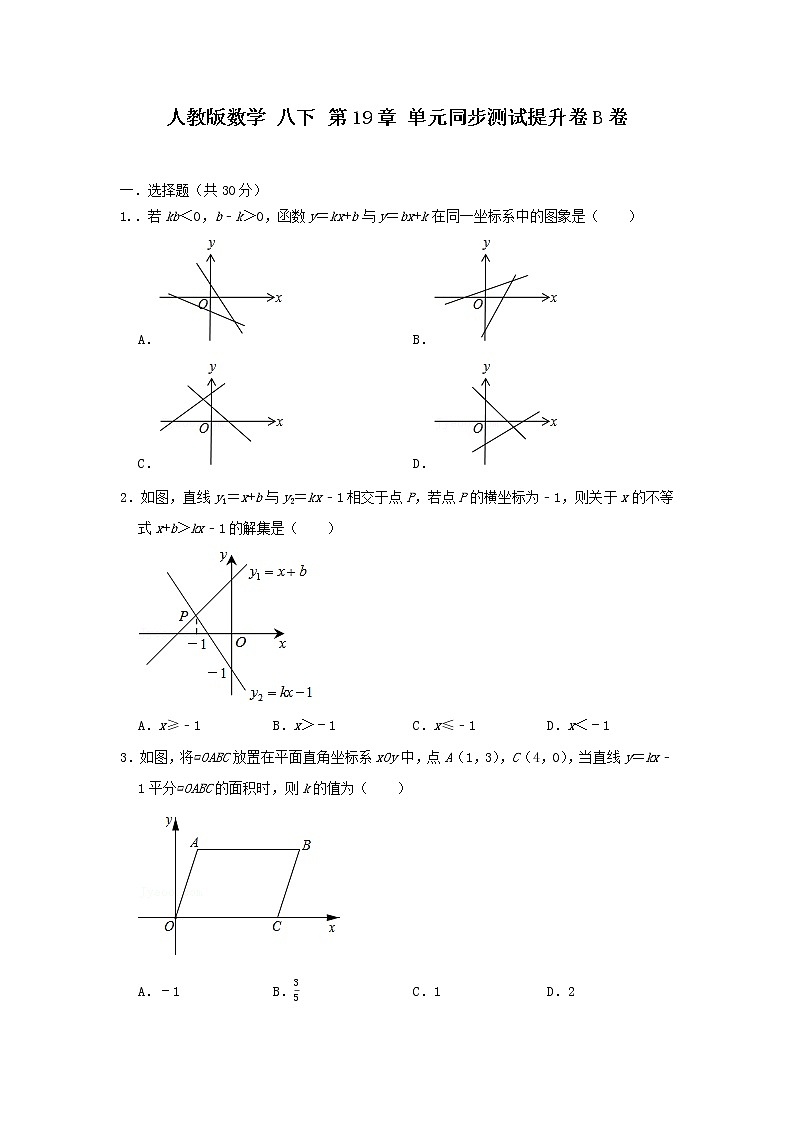
1.．若kb＜0，b﹣k＞0，函数y＝kx+b与y＝bx+k在同一坐标系中的图象是（　　）

A． B． 

C． D．

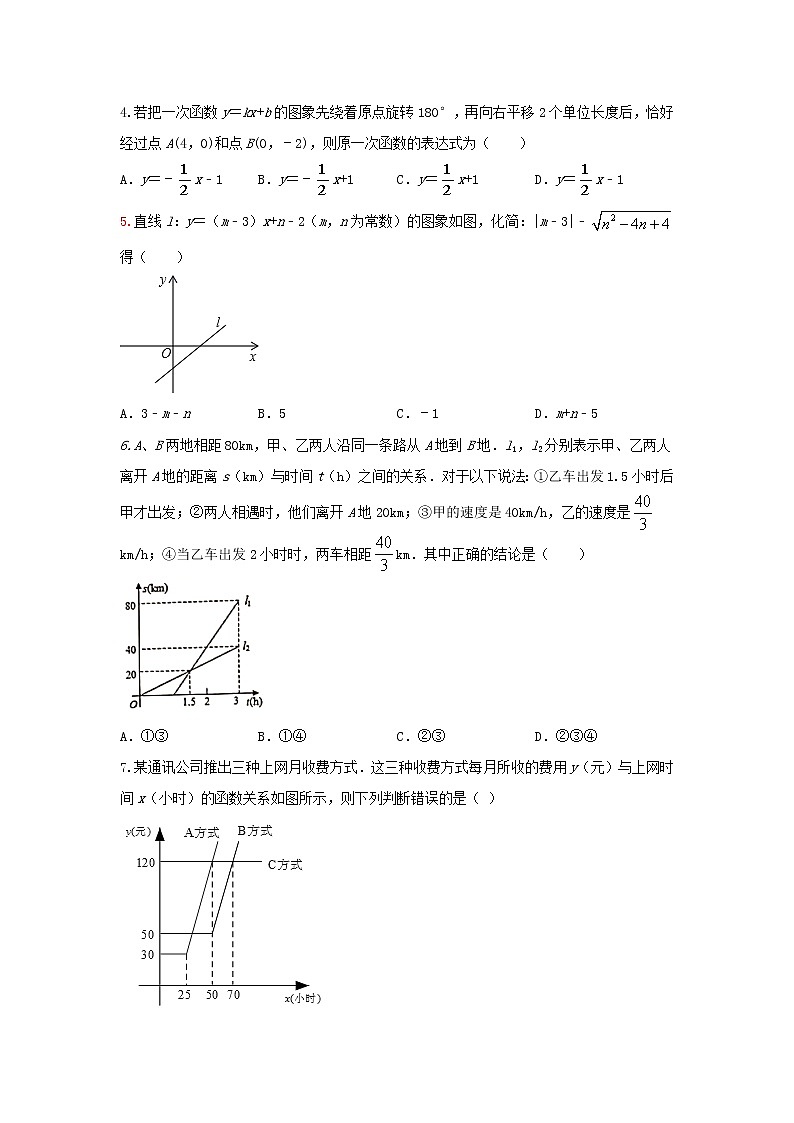
2．如图，直线y1＝x+b与y2＝kx﹣1相交于点P，若点P的横坐标为﹣1，则关于x的不等式x+b＞kx﹣1的解集是（　　）

A．x≥﹣1 B．x＞﹣1 C．x≤﹣1 D．x＜﹣1

3．如图，将▱OABC放置在平面直角坐标系xOy中，点A（1，3），C（4，0），当直线y＝kx﹣1平分▱OABC的面积时，则k的值为（　　）

A．﹣1 B． C．1 D．2

4.若把一次函数y＝kx+b的图象先绕着原点旋转180°，再向右平移2个单位长度后，恰好经过点A(4，0)和点B(0，﹣2)，则原一次函数的表达式为（　　）

A．y＝﹣x﹣1 B．y＝﹣x+1 C．y＝x+1 D．y＝x﹣1

5.直线l：y＝（m﹣3）x+n﹣2（m，n为常数）的图象如图，化简：|m﹣3|﹣得（　　）

A．3﹣m﹣n B．5 C．﹣1 D．m+n﹣5

6.A、B两地相距80km，甲、乙两人沿同一条路从A地到B地．l1，l2分别表示甲、乙两人离开A地的距离s（km）与时间t（h）之间的关系．对于以下说法：①乙车出发1.5小时后甲才出发；②两人相遇时，他们离开A地20km；③甲的速度是40km/h，乙的速度是km/h；④当乙车出发2小时时，两车相距km．其中正确的结论是（    ）

A．①③ B．①④ C．②③ D．②③④

7.某通讯公司推出三种上网月收费方式．这三种收费方式每月所收的费用y（元）与上网时间x（小时）的函数关系如图所示，则下列判断错误的是（ ）

A．每月上网不足25小时，选择A方式最省钱

B．每月上网时间为30小时，选择B方式最省钱

C．每月上网费用为60元，选择B方式比A方式时间长

D．每月上网时间超过70小时，选择C方式最省钱

8.快车从甲地驶往乙地，慢车从乙地驶往甲地，两车同时出发并且在同一条公路上匀速行驶．图中折线表示快、慢两车之间的路程与它们的行驶时间之间的函数关系．小欣同学结合图象得出如下结论：快车途中停留了；快车速度比慢车速度快；图中；快车先到达目的地．其中正确的是

1. 
    B.  C.  D.

9.甲、乙两车从城出发匀速行驶至城．在整个行驶过程中，甲、乙两车离开城的距离千米与甲车行驶的时间小时之间的函数关系如图所示．则下列结论：

，两城相距千米；              

乙车比甲车晚出发小时，却早到小时；

乙车出发后小时追上甲车；

当甲、乙两车相距千米时，或．

其中正确的结论有

1. 个 B. 个 C. 个 D. 个

10.如图，在平面直角坐标系中，点、、在轴上，、、在直线上，若，且、、都是等边三角形，从左到右的小三角形阴影部分的面积分别记为、、、、则可表示为

A.  B.  C.  D.

二．填空题（共24分）

11.直线l1：y＝ax﹣b与直线l2：y＝﹣kx在同一平面直角坐标系中的图象如图所示，则关于x的不等式﹣ax+b＞kx的解集为 　　．

12.已知平面直角坐标系中，O为坐标原点，点A的坐标为(0，8)，点B的坐标为(4，0)，点E是直线y=x＋4上的一个动点，若∠EAB=∠ABO，则点E的坐标为________．

13.若点A(m，n)在直线y＝kx(k≠0)上，当－1≤m≤1时，－1≤n≤1，则这条直线的函数解析式为________．

14.已知直线y1=x，y2=x+1，y3=﹣x+5的图象如图所示，若无论x取何值，y总取y1，y2，y3中的最小值，则y的最大值为　    　．

15.已知一次函数y1＝kx＋b与y2＝x＋a的图象如图所示，则下列结论：①k＜0；②a＞0；③b＜0；④关于x的方程kx＋b＝x＋a的解为x＝3；⑤x＞3时，y1＜y2，其中正确的结论是_____．（只填序号）

16.如图，一次函数与轴交于点，与轴交于点．点的坐标为，若点在直线上，点在轴上，若以、、、为顶点的四边形为平行四边形，则点的坐标为______．

三．解答题（共66分）

17.（6分）某学校组织学生到离校的光明科技馆去参观，学生小明因事没能乘上学校的包车，于是准备在学校门口改乘出租车去光明科技馆，出租车的收费标准如下表：

写出出租车行驶的路程与收费元之间的函数关系式．

小明身上仅有元钱，乘出租车到光明科技馆的车费够不够请说明理由．
 

18.（8分）如图，直线l1在平面直角坐标系中与y轴交于点A，点B（﹣3，3）也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C也在直线l1上．

（1）求点C的坐标和直线l1的解析式；

（2）已知直线l2：y＝x+b经过点B，与y轴交于点E，求△ABE的面积．

19.（8分）如图，直线经过点．

（1）求直线的表达式；

（2）若直线与直线相交于C，求点C的坐标；

（3）根据图像，写出关于x的不等式的解集．

20.（10分）如图，在平面直角坐标系xOy中，直线yx+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．

（1）求AB的长；

（2）求点C和点D的坐标；

（3）y轴上是否存在一点P，使得S△PABS△OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．

21.（10分）已知一次函数表达式为（为常数）．

（1）求证：该一次函数一定经过定点．

（2）当图象不经过第一象限时，求m的取值范围．

（3）在（2）的条件下，求其中任意两条直线与y轴围成的三角形面积的取值范围．

22.（12分）2020年武汉发生新冠肺炎疫情，“一方有难，八方支援”，我省迅速组织一百多名医护志愿者并捐赠一批医疗物资从南昌出发前往湖北随州支援抗疫，南昌、随州两地相距500千米，大巴与货车走同一条路线，图中线段和折线分别表示大巴和货车行驶的路程s与行驶时间t之间的关系，根据图象回答下列问题：

（1）________更早出发，早出发________小时；

（2）大巴的速度是_______千米时：

（3）货车出发4小时后，两车相距多少千米？

（4）大巴车出发后，用多长时间追上了货车？

23.（12分）甲仓库有水泥110吨，乙仓库有水泥70吨，现要将这些水泥全部运往A，B两工地，调运任务承包给某运输公司，已知A工地需水泥100吨，B工地需水泥80吨，从甲仓库运往A，B两工地的路程和每吨每千米的运费如表：

（1）设甲仓库运往A地水泥x吨，则甲仓库运往B地水泥_________吨，乙仓库运往A地水泥_________吨，乙仓库运住B地水泥_________吨（用含x的代数式表示）；

（2）求总运费W关于x的函数关系式，并求出自变量的取值范围；

（3）当甲、乙两仓库各运往A，B两工地多少吨水泥时，总运费最省？最省的总运费是多少？