广东省惠州市德兴通中英文学校2022-2023学年八年级下学期开学考试数学试题

这是一份广东省惠州市德兴通中英文学校2022-2023学年八年级下学期开学考试数学试题，共10页。试卷主要包含了单选题，填空题，解答题等内容，欢迎下载使用。
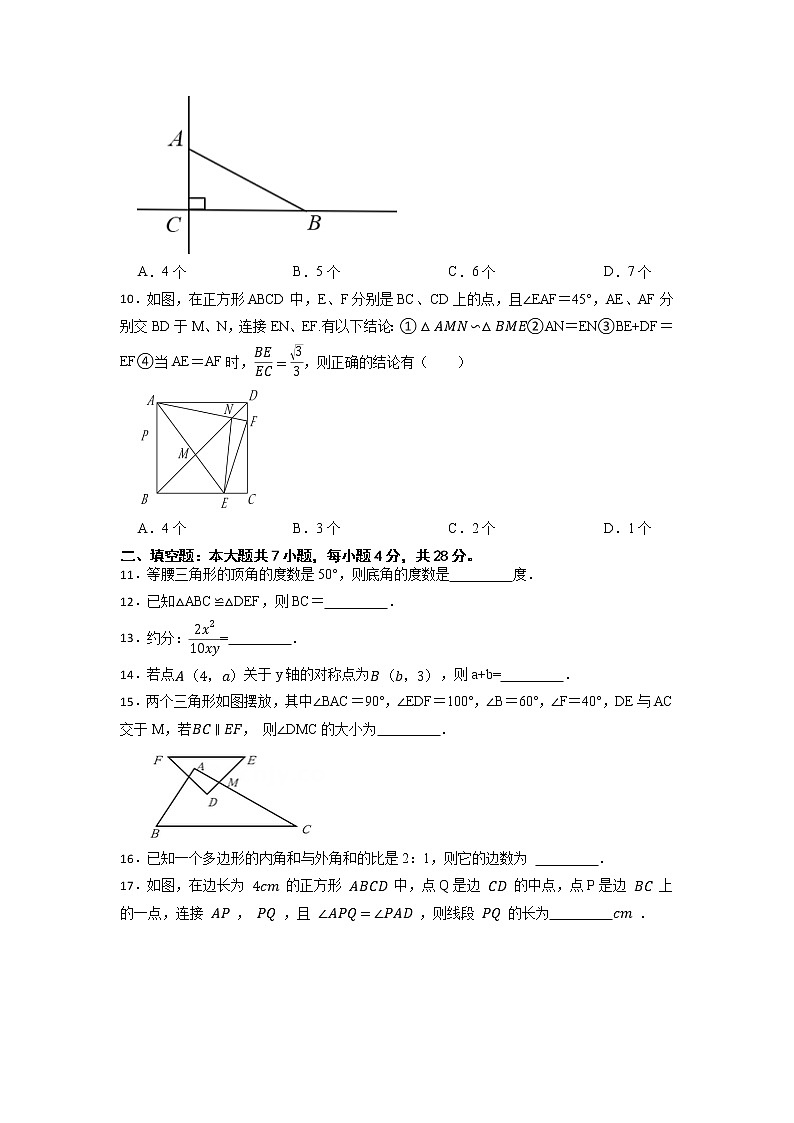
2022-2023学年度第二学期惠阳区德兴通学校寒假收心卷八年级数学一、单选题：本大题共10小题，每小题3分，共30分。1．下列图形既是轴对称图形，又是中心对称图形的是（　　）A．平行四边形 B．三角形 C．等腰三角形 D．矩形2．平面直角坐标系内的点A（﹣3，﹣2）与点B（3，﹣2）关于（　　）A．y轴对称 B．x轴对称 C．原点对称 D．无法确定3．在△ABC中，如果∠A﹣∠B＝90°，那么△ABC是（　　）A．直角三角形 B．钝角三角形 C．锐角三角形 D．斜三角形4．分式与的最简公分母是（　　）A． B．C． D．5．下列各组线段中，不能构成直角三角形的一组是（　　）A．，1， B．1，，2 C．6，8，10 D．4，4，56．下列四个图标中是轴对称图形的是（　　）A． B． C． D．7．如果一个多边形的内角和等于一个三角形的外角和的两倍，那么这个多边形是(　　)  A．三角形 B．四边形 C．五边形 D．六边形8．下列各式从左到右变形正确的是（　　）A． B． C． D．9．如图，已知直角三角形ABC中，∠ACB=90°，∠CAB=60°，在直线BC或AC上取一点P，使得△ABP为等腰三角形，则符合条件的点有（　　）A．4个 B．5个 C．6个 D．7个10．如图，在正方形ABCD中，E、F分别是BC、CD上的点，且∠EAF＝45°，AE、AF分别交BD于M、N，连接EN、EF.有以下结论：①②AN＝EN③BE+DF＝EF④当AE＝AF时，，则正确的结论有（　　）A．4个 B．3个 C．2个 D．1个二、填空题：本大题共7小题，每小题4分，共28分。11．等腰三角形的顶角的度数是50°，则底角的度数是　     　度．12．已知△ABC≌△DEF，则BC＝　     　．13．约分：=　     　．14．若点关于y轴的对称点为，则a+b=　     　．15．两个三角形如图摆放，其中∠BAC＝90°，∠EDF＝100°，∠B＝60°，∠F＝40°，DE与AC交于M，若， 则∠DMC的大小为　     　．16．已知一个多边形的内角和与外角和的比是2：1，则它的边数为 　     　．17．如图，在边长为 的正方形 中，点Q是边 的中点，点P是边 上的一点，连接 ， ，且 ，则线段 的长为　     　 ．  三、解答题：第18,19,20小题6分，第21，22，23小题8分，第24，25小题10分。18．先化简，再求值：，其中．19．如图，点在同一直线上，求证：20．如图，在中，是边上的高线，是一条角平分线，它们相交于点P.已知，，求的度数.21．如图，已知点E，F在线段AB上，，，.求证：.22．如图，A，B两点分别位于一个池塘的两端，小明通过构造△ABC与△BCD来测量A，B间的距离，其中，.那么量出的BD的长度就是AB的距离.请你判断小明这个方法正确与否，并给出相应理由.23．如图，△ABC中，点O为AC边上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的外角平分线CF于点F，交∠ACB内角平分线CE于E.（1）求证：EO=FO；   （2）当点O运动到何处时，四边形AECF是矩形？并证明你的结论；   （3）若AC边上存在点O，使四边形AECF是正方形，猜想△ABC的形状并证明你的结论。   24．如图，在△ABC中，BC=7cm，AC=24cm，AB=25cm，P点在BC上，从B点到C点运动（不包括C点），点P运动的速度为2 cm/s；Q点在AC上从C点运动到A点（不包括A点），速度为5 cm/s.若点P，Q分别从B，C同时运动，请解答下面的问题：（1）经过多少时间后，P，Q两点间的距离为   cm？（2）经过多少时间后，△PCQ的面积为15 cm2？（3）设运动时间为t，用含t的代数式表示△PCQ的面积，并用配方法说明t为何值时△PCQ的面积最大，最大面积是多少？25．已知：AD是△ABC的角平分线，点E为直线BC上一点，BD=DE，过点E作EF∥AB交直线AC于点F，当点F在边AC的延长线上时，如图①易证AF+EF=AB；当点F在边AC上，如图②；当点F在边AC的延长线上，AD是△ABC的外角平分线时，如图3．写出AF、EF与AB的数量关系，并对图②进行证明．
答案解析部分1．【答案】D2．【答案】A3．【答案】B4．【答案】D5．【答案】D6．【答案】C7．【答案】D8．【答案】D9．【答案】C10．【答案】B11．【答案】6512．【答案】EF13．【答案】14．【答案】－115．【答案】110°16．【答案】617．【答案】18．【答案】解：原式将代入，原式19．【答案】证明：即在与中，20．【答案】解：∵，∴，∵，∴，∵是一条角平分线，∴，∴.21．【答案】证明：，，即，，和都是直角三角形，在和中，，，．22．【答案】解：根据题意，在和中∴≌∴∴小明这个方法正确.23．【答案】（1）证明：∵CE平分∠ACB，  ∴∠ACE=∠BCE，∵MN∥BC，∴∠OEC=∠ECB，∴∠OEC=∠OCE，∴OE=OC，同理，OC=OF，∴OE=OF．（2）解：当点O运动到AC中点处时，四边形AECF是矩形．  如图AO=CO，EO=FO，∴四边形AECF为平行四边形，∵CE平分∠ACB，∴∠ACE= ∠ACB，同理，∠ACF= ∠ACG，∴∠ECF=∠ACE+∠ACF= （∠ACB+∠ACG）= ×180°=90°，∴四边形AECF是矩形．（3）解：△ABC是直角三角形  ∵四边形AECF是正方形，∴AC⊥EN，故∠AOM=90°，∵MN∥BC，∴∠BCA=∠AOM，∴∠BCA=90°，∴△ABC是直角三角形．24．【答案】（1）解：连接PQ 设经过ts后，P. Q两点的距离为 ，ts后， ， ，根据勾股定理可知 ，代入数据 解得 或 (不合题意舍去) ；（2）解：设经过t s后， 的面积为 ts后， ， ，解得 ， 经过2或1.5s后， 的面积为 .（3）解：设经过ts后，△PCQ的面积最大， ts后， ， ∴当 时，△PCQ的面积最大， 最大面积是 25．【答案】解：当点F在边AC的延长线上时，延长EF、AD相交于点G，如图：∵AD是△ABC的角平分线，∴∠BAD=∠CAD，∵EF∥AB，∴∠BAD=∠G，∠B=∠E，∴∠CAD=∠G，∴FA=FG，在△ABD和△GED中，，∴△ABD≌△GED(AAS)，∴AB=EG，∴AF+EF=FG+EF=EG=AB；当点F在边AC上，延长FE、AD相交于点H，如图：∵AD是△ABC的角平分线，∴∠BAD=∠CAD，∵EF∥AB，∴∠BAD=∠H，∠B=∠DEH，∴∠CAD=∠H，∴FA=FH，在△ABD和△HED中，，∴△ABD≌△HED(AAS)，∴AB=EH，∴AF-EF=FH-EF=EH=AB；当点F在边AC的延长线上，AD是△ABC的外角平分线时，如图：延长AD交EF于点I，∵AD是△ABC的外角平分线，∴∠JAD=∠CAD，∵EF∥AB，∴∠JAD=∠AIF，∠B=∠E，∴∠CAD=∠AIF，∴FA=FI，在△ABD和△IED中，，∴△ABD≌△IED(SAS)，∴AB=EI，∴EF- AF= EF-IF=EI=AB．