











初中数学人教版八年级下册17.1 勾股定理完美版ppt课件
展开17.1 勾股定理(第3课时)
一、单选题
1.如图所示,中,,长度为单位1,数轴上点A所表示的数为a,则a的值是( )
A. B. C. D.
2.已知平面直角坐标系中有A(1,1),B(4,4)两点,则连接两点的线段AB的长为( )
A.3 B. C.4 D.5
3.如图,在的方格纸,每个小正方形边长均为1,已知点A,B在方格顶点上,则长为( )
A. B. C.2 D.
4.如图,边长为1的正方形网格图中,点A,B都在格点上,若,则BC的长为( )
A. B. C. D.
5.如图1,小正方形边长为1,连接小正方形的三个顶点,可得△ABC,则AC边上的高是( )
A. B. C. D.
6.在中, ,则的面积为( ).
A. B. C.或 D.或
7.已知Rt△ABC中,∠C=90°,AC=1,BC=3,则AB的取值范围是( )
A.3.0<AB<3.1 B.3.1<AB<3.2
C.3.2<AB<3.3 D.3.3<AB<3.4
8.如图,在ABC中,∠B=22.5°,∠C=45°,若AC=2,则ABC的面积是( )
A. B.1+ C.2 D.2+
9.平面直角坐标系xOy中,已知,两点,C为x轴上一动点,则周长的最小值为( )
A. B. C.5 D.
10.图1是第七届国际数学教育大会(ICME-7)的会徽图案,它是由一串有公共顶点O的直角三角形(如图2)演化而成的.如图2中的,按此规律,在线段,,,…中, 长度为整数的线段有( )条.
A.3 B.4 C.5 D.6
二、填空题
11.如图,在数轴上点A表示的实数是__.
12.如图,将5个边长为1的小正方形组成的图形纸剪开,拼成一个大正方形ABCD,以A为圆心,AB为半径作弧,与数轴正半轴交于点P,则点P表示的数为________.
13.若,另一点在轴上,到轴的距离等于到原点的距离,则点坐标为_____.
14.如图,数轴上点所表示的数为1,点,,是4×4的正方形网格上的格点,以点为圆心,长为半径画圆交数轴于,两点,则点所表示的数为 ___________.(可以用含根号的式子表示)
15.如图,在的网格中,每个小正方形的边长都是1个单位长度,点O,A,B,C在网格的交点(格点)上,点,在第三象限内的格点上找一点D,使与全等,则点D的坐标为______.
16.如图,在中,,,平分,,,则的周长________.
17.课本中有这样一句话:“利用勾股定理可以作出,,…线段(如图所示).”即:,过A作且,根据勾股定理,得;再过作且,得;…以此类推,得________.
18.如图,D是等边三角形外一点,,,当长最大时,的面积为____________.
三、解答题
19.如图,,在数轴上点A所表示的数为a,求a的值.
20.如图,正方形网格中的每个小正方形边长都是1,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1)在图1中,画一个三角形,使它的三边长都是有理数;
(2)在图2中,画一个三角形,使它的三边长都是无理数.
21.(1)如图①,数轴上的点A、B表示的数分别是什么?
(2)利用(1)中的方法,在图②数轴上分别描出表示,的点.
22.如图,纸上有五个边长为的小正方形组成的图形纸,我们可以把它剪开拼成一个正方形.
(1)拼成的正方形的边长为______.
(2)如图,以数轴的单位长度的线段为边作一个直角三角形,以数轴上表示的点为圆心,直角三角形的最大边为半径画弧,交数轴正半轴于点,那么点表示的数是______.
(3)如图,网格中每个小正方形的边长为,若能把阴影部分剪拼成一个新的正方形,求新的正方形的面积和边长.
23.实数和数轴上的点一一对应,无理数也可以在数轴上表示出来.
(1)如图,点O是原点,点A在数轴上,且点A对应的实数为-2,过点A作AB垂直于数轴,且AB=1,连接OB,以O为圆心,OB长为半径画弧,交数轴于点C,那么点C对应的实数为___________;
(2)在(1)的条件下,若将线段OC向右平移,使得O点对应的实数为1,那么此时C点对应的实数为___________;
(3)如图,射线AB垂直数轴于点A,点A对应的数是3,请按照(1)中的方法,在数轴上用尺规作出表示的点C(不写作法,保留作图痕迹).
24.在4×4的网格中,每个小正方形的边长为1,请在甲,乙,丙三个方格图中,分别按照要求画一个格点三角形(三个顶点都在格点上的三角形叫格点三角形).
(1)请在图甲中作△DEF与△ABC全等.
(2)请在图乙中作格点三角形与△ABC全等,且所作的三角形有一条边经过MN的中点.
(3)请在图丙中作格点△PQR与△ABC不全等但面积相等.
25.如图,在中,,平分交于点D,过点D作交于点E.
(1)求证:;
(2)如果,,求的长.
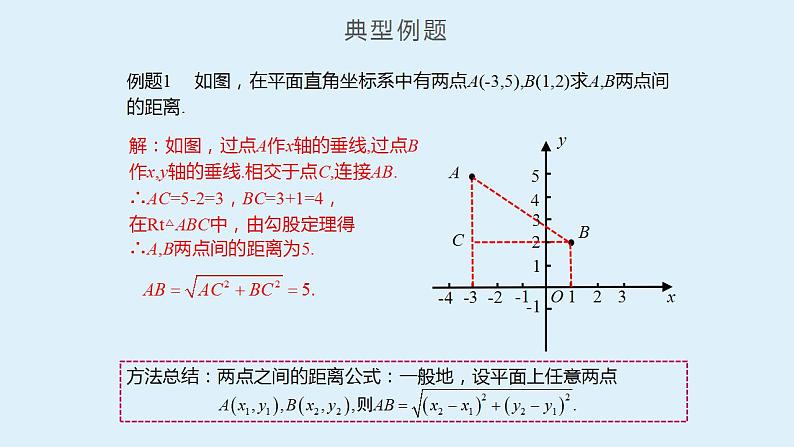
26.先阅读下列文字,再回答后面的问题:已知在平面直角坐标系内有两点,其两点间的距离可用公式表示,同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为或.
(1)已知A(2,4)、B(-3,8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离.
27.在学习了勾股定理后,数学兴使小组在江老师的引导下,利用正方形网格和勾股定理运用构图法进行了一系列探究活动:
(1)在中,、、三边的长分别为、、,求的面积.如图1,在正方形网格(每个小正方形的边长为1)中,画出格点(即三个顶点都在小正方形的顶点处),不需要求的高,借用网格就能计算出它的面积,这种方法叫做构图法.则的面积为___________.
(2)在平面直角坐标系中,①若点A为,点B为,则线段的长为___________;②若点A为,点B为,则线段的长可表示为__________∶
(3)在图2中运用构图法画出图形,比较大小:_______(填“>”或“<”);
(4)若三边的长分别为、、(,.且),请在如图3的长方形网格中(设每个小长方形的长为m,宽为n),运用构图法画出,并求出它的面积(结果用m,n表示).
28.对于平面直角坐标系中的线段及点,给出如下定义:
若点满足,则称为线段的“轴点”,其中,当时,称为线段的“远轴点”;当时,称为线段的“近轴点”.
(1)如图1,点,的坐标分别为,,则在,,,中,线段的“近轴点”是________.
(2)如图2,点的坐标为,点在轴正半轴上,且
①若为线段的“远轴点”,直接写出点的横坐标的取值范围________;
②点为轴上的动点(不与点重合且),若为线段的“轴点”,当线段与的和最小时,求点的坐标.
29.如图1,在中,,,.
(1)求证:;
(2)如图2,交于点P,若,求证:A,O,D三点共线;
(3)如图3,在(2)的条件下,若于H,过点O作于E,,,求,的长度.
数学八年级下册17.1 勾股定理备课ppt课件: 这是一份数学八年级下册17.1 勾股定理备课ppt课件,共26页。PPT课件主要包含了求得结果,知识回顾,学习目标,课堂导入,点A表示的数字为-2,点B表示的数字为-1,点C表示的数字为1,点D表示的数字为2,数轴上的点,一一对应等内容,欢迎下载使用。
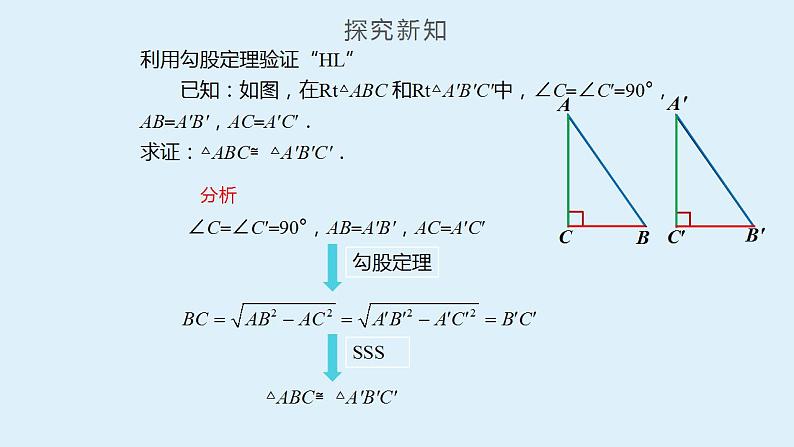
数学八年级下册第十七章 勾股定理17.1 勾股定理教课ppt课件: 这是一份数学八年级下册第十七章 勾股定理17.1 勾股定理教课ppt课件,共16页。PPT课件主要包含了复习引入,∠C90°,不满足,解决问题,巩固练习,课堂小结,布置作业等内容,欢迎下载使用。
人教版八年级下册17.1 勾股定理示范课课件ppt: 这是一份人教版八年级下册17.1 勾股定理示范课课件ppt,共21页。PPT课件主要包含了情境引入,探究新知,如何证明这个命题,拓展应用,我们应先求出什么量,先求出对角线,线段BD,线段OBOD,怎么求OBOD呢,类题运用等内容,欢迎下载使用。











