初中数学中考复习 2020年中考数学专题复习：三大几何变换

这是一份初中数学中考复习 2020年中考数学专题复习：三大几何变换，共11页。

知识互联网

题型一：平移变换
思路导航
平移一般是在需要同时移动两条线段或元素的时候，才考虑的方法．
典题精练
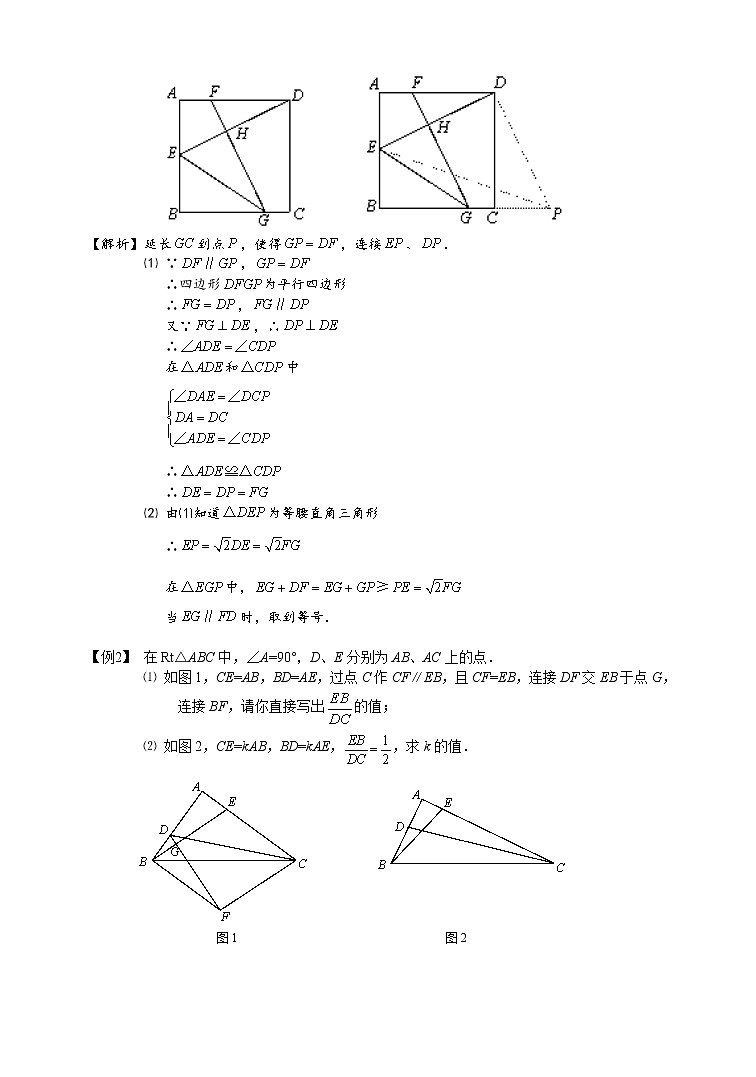
已知：如图，正方形中，是上一点，于点．⑴ 求证：．
⑵ 求证：．

延长到点，使得，连接、．
⑴ ∵，
∴四边形为平行四边形
∴，
又∵，∴
∴
在和中
∴
∴
⑵ 由⑴知道为等腰直角三角形
∴
在中，
当时，取到等号．
在Rt△ABC中，∠A=90°，D、E分别为AB、AC上的点．
⑴ 如图1，CE=AB，BD=AE，过点C作CF∥EB，且CF=EB，连接DF交EB于点G，连接BF，请你直接写出的值；
⑵ 如图2，CE=kAB，BD=kAE，，求k的值．
图2
图1
【解析】(1).
(2)过点C作CF∥EB且CF=EB，连接DF交EB于点G, 连接BF.
∴四边形EBFC是平行四边形.
∴CE∥BF且CE=BF.
∴∠ABF=∠A=90°.
∵BF=CE=kAB.∴.
∵BD=kAE，
∴.
∴.
∴∽.
∴,∠GDB=∠AEB.
∴∠DGB=∠A=90°.
∴∠GFC=∠BGF=90°.
∵.
∴.
∴k=.
题型二：轴对称变换
典题精练
⑴如图，已知正方形纸片的边长为，的半径为，圆心在正方形的中心上，将纸片按图示方式折叠，使恰好与相切于点（与除切点外无重叠部分），延长交边于点，则的长是 ．
⑵将弧沿弦折叠交直径于点，若，则的长是______________．
⑴ 过点作于．
则四边形是矩形，∴，
设，则根据对称性可知
∴，
在中，，
∴，即，
解得，∴．
⑵ 将半圆还原，点关于的对称点为，
作于．
根据“翻折”的性质可知，
则
∵，
则，
BC2=BH·AB
∴．
把正方形沿着折叠使点落在上，交于点，已知正方形的边长为，求的周长．
在上取点，使，连接．
∵，∴
由翻折得对称性可知
∴
在和中
∴
∴，
在和中
∴
∴
∴的周长为．
题型三：旋转变换
典题精练
在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．
⑴ 当点O为AC中点时，
①如图1， 三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系（无需证明）；
②如图2， 三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的猜想是否成立．若成立，请证明；若不成立，请说明理由；
⑵ 当点O不是AC中点时，如图3,，三角板的两直角边分别交AB，BC于E、F两点，若，求的值．
C
O
B
A
O
E
图1
F
B
A
O
C
E
F

A
B
C
E
F
图2
图3
C
B
A
O
E
F
【解析】（1）
猜想：.
成立.
证明：连结OB.
∵AB=BC , ∠ABC=90°,O点为AC的中点，
∴,∠BOC=90°,∠ABO=∠BCO=45°.
∵∠EOF=90°，∴∠EOB=∠FOC. 又∵∠EBO=∠FCO，
∴△OEB≌△OFC（ASA）.∴BE=CF.
又∵BA=BC, ∴AE=BF.
在RtΔEBF中，∵∠EBF=90°, ..
（2）解：如图，过点O作OM⊥AB于M，ON⊥BC于N.
A
O

B
C
E
F
M
N
∵∠B=90°, ∴∠MON=90°.
∵∠EOF=90°,
∴∠EOM=∠FON.
∵∠EMO=∠FNO=90°，∴△OME∽△ONF.
∴
∵△AOM和△OCN为等腰直角三角形，
∴△AOM∽△OCN ∴.
∵， ∴.
和是绕点旋转的两个相似三角形，其中与、与为对应角．
⑴如图1，若和分别是以与为顶角的等腰直角三角形，且两三角形旋转到使点、、在同一条直线上的位置时，请直接写出线段与线段的关系；
⑵若和为含有角的直角三角形，且两个三角形旋转到如图2的位置时，试确定线段与线段的关系，并说明理由；
⑶若和为如图3的两个三角形，且，，在绕点旋转的过程中，直线与夹角的度数是否改变？若不改变，直接用含、的式子表示夹角的度数；若改变，请说明理由．
⑴ 线段与线段的关系是．
⑵ 如图2，连接、并延长，设交点为点．
∵ ，∴，∴．
∵，∴，．∴ ．
∴ ．∴．
在中，，
∵，∴．
又∵∴，
∴．
∵，∴，
∴， ∴，∴．
即．
⑶ 在绕点旋转的过程中，直线与夹角度数不改变，度．
复习巩固
题型一 平移变换 巩固练习
如图，已知，，若，则的度数为______．
. 通过作平行线平移角，使角与角之间联系起来．
A
如下图，两条长度为的线段和相交于点，且，求证：．

考虑将、和集中到同一个三角形中，以便运用三角形的不等关系．
作且，则四边形是平行四边形，从而．
（教师可告诉学生：一组对边平行且相等的四边形是平行四边形），
在中可得，
即．
由于，，
所以是等边三角形，故，所以．
题型二 轴对称变换 巩固练习
如图矩形纸片，，，上有一
点，，上有一点，，过作
交于，将纸片折叠，使点与点重合，折
痕与交于点，则的长是________cm．
. 解法：过Q作QM⊥DC，设QP=x，∴QE=x，∵DE=2，∴
∴在Rt△QME中，，∴
题型三 旋转变换 巩固练习
已知正方形中，点在边上，，（如图所示） 把线段绕
点旋转，使点落在直线上的点处，则、两点的距离为 ．

或．
题目里只说“旋转”，并没有说顺时针还是逆时针，而且说的是“直线上的点”，所以有两种情况如图所示：顺时针旋转得到点，则，逆时针旋转得到点，则，．
在平面直角坐标系中，矩形的顶点、的坐标分别为和．将矩形 绕点顺时针旋转度，得到四边形，使得边与轴交于点，此时边、分别与边所在的直线相交于点、．
⑴ 如图1，当点与点重合时，求点的坐标；
⑵ 在⑴的条件下，求的值；
⑶ 如图2，若点与点不重合，则的值是否发生变化？若不变，试证明你的结论；若有变化，请说明理由．
（图1）
（图2）
（北京东城期末）

⑴ ∵将矩形绕点顺时针旋转度，得到四边形，
且、的坐标分别为和，
∴，．
（图1）
∴．
∴点的坐标为．
⑵ ∵，，
∴．
∵，且，
∴．同理．
∴，∴．
（或：∵．∴．）
⑶ 如图2所示，作交于点，
∵，且，
∴四边形是平行四边形．
（图2）
∴．
∵，
∴．
∴．
又∵，
∴．
∴．
∴的值不会发生改变．
课后测
【测试1】在四边形中，，，和的长度分别为和，那么的长为________．
【解析】自点作交于，
则四边形是平行四边形，，．又．
所以，是等腰三角形．
，
所以．
【测试2】如图，已知中，，，点在边上，把沿翻折使与重合，得，则与重叠部分的面积为（ ）
A．B．C．D．
【解析】A
【测试3】如图，正方形与正三角形的顶点重合，将绕顶点旋转，在旋转过程中，当时，的大小可以是________．
【解析】或