高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算多媒体教学课件ppt

这是一份高中数学人教A版 (2019)必修 第二册6.2 平面向量的运算多媒体教学课件ppt，共26页。PPT课件主要包含了数乘定义，复习回顾，向量的夹角，例1已知，θ90º，θ0º，θ180º，︱cosθ︱≤1，牛刀小试，为钝角三角形等内容，欢迎下载使用。
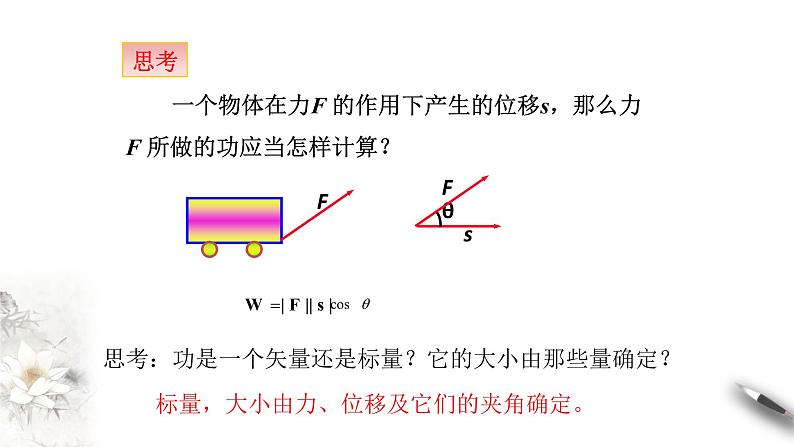
一个物体在力F 的作用下产生的位移s，那么力F 所做的功应当怎样计算？
思考：功是一个矢量还是标量？它的大小由那些量确定？
标量，大小由力、位移及它们的夹角确定。
思考：如果我们将公式中的力与位移类比推广到两个一般向量，其结果又该如何表述？
两个向量的大小及其夹角余弦的乘积。
　　功是力与位移的大小及其夹角余弦的乘积；
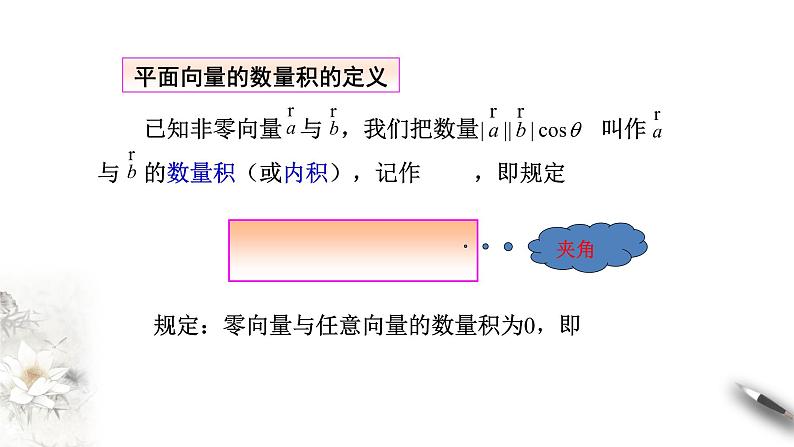
平面向量的数量积的定义
（1）两向量的数量积是一个数量，而不是向量，符号由夹角决定.
（3） 在运用数量积公式解题时，一定要注意两向量夹角的范围是 [ 0°，180°]．
思考：向量的数量积是一个数量，那么它什么时候为正，什么时候为负？
数量积符号由cs的符号所决定
解：由 得
因为 所以 。
这种变换为向量 向向量 投影，
叫做向量 在向量 上的投影向量
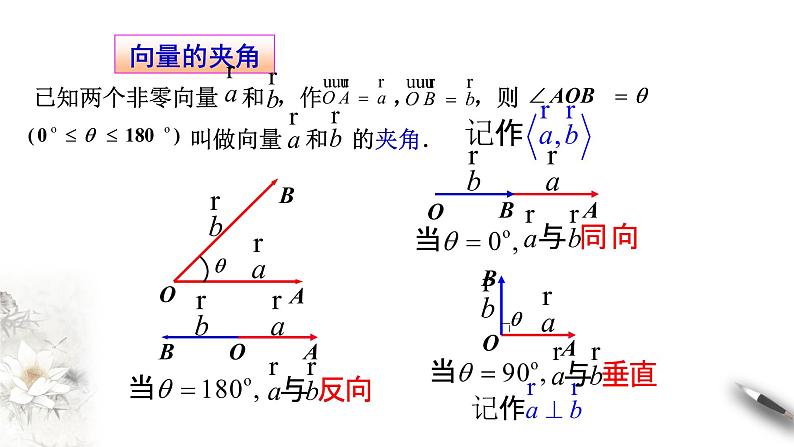
探究：如图，设与 方向相同的单位向量为 ， 与 的夹角为 ，那么 与 之间有怎样的关系？
当 为锐角时，
当 为直角时，
当 为钝角（如图（3））时，
当 时，
当 时，
综上，对任意的 都有
设 是非零向量，它们的夹角是 ， 是与 方向相同的单位向量，则
4.已知 为单位向量，且 的夹角 为 ，求向量 在 上的投影向量。
解：向量 在 上的投影向量为
1、向量的数量积的定义
规定：零向量与任意向量的数量积为0，即 0．
5. 常用︱a︱＝ 求向量的模.　　　　常用　　　　　　求向量的夹角.