七下数学专题 平行线的判定与性质（考点突破）

这是一份七下数学专题 平行线的判定与性质（考点突破），共39页。
平行线的判定与性质
【考点导航】
目录
【典型例题】 1
【考点一 同位角、内错角、同旁内角的辨别】 1
【考点二 平行线的判定】 2
【考点三 添加一条件使两条直线平行】 4
【考点四 平行线的性质】 5
【考点五 根据平行线的性质与判定求角度】 7
【考点六 平行线的性质在生活中的应用】 9
【考点七 平行线的性质与判定综合应用】 12
【过关检测】 15

【典型例题】
【考点一 同位角、内错角、同旁内角的辨别】
例题：（2022·全国·七年级课前预习）如图，在所标识的角中，∠1与____是同位角，∠2与_____是内错角，∠5与____是同旁内角．

【变式训练】
1．（2021·全国·七年级课时练习）如图所示，与是_________角，是直线________和直线________被直线_____所截而形成的，与是_____角，是直线________和直线___________被直线__________所截而形成的．

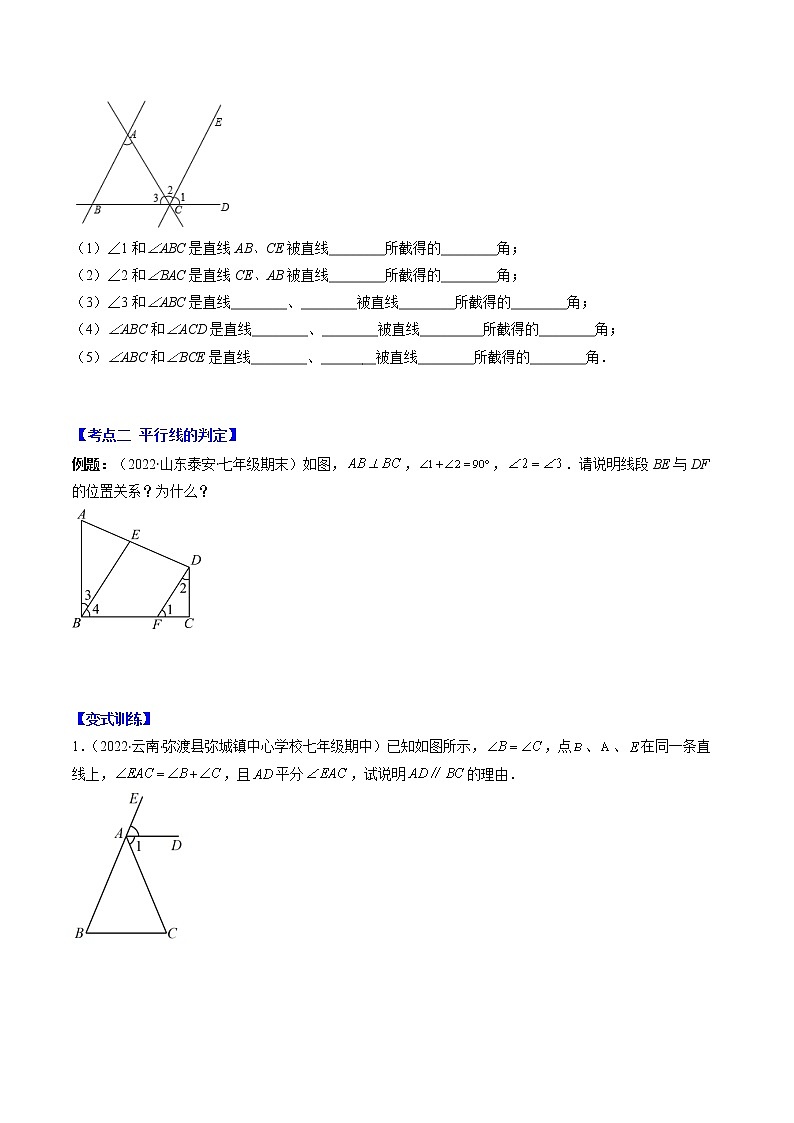
2．（2022·全国·七年级）如图，

（1）∠1和∠ABC是直线AB、CE被直线________所截得的________角；
（2）∠2和∠BAC是直线CE、AB被直线________所截得的________角；
（3）∠3和∠ABC是直线________、________被直线________所截得的________角；
（4）∠ABC和∠ACD是直线________、________被直线_________所截得的________角；
（5）∠ABC和∠BCE是直线________、________被直线________所截得的________角．


【考点二 平行线的判定】
例题：（2022·山东泰安·七年级期末）如图，，，．请说明线段BE与DF的位置关系？为什么？




【变式训练】
1．（2022·云南·弥渡县弥城镇中心学校七年级期中）已知如图所示，，点、、在同一条直线上，，且平分，试说明的理由．




2．（2022·山东·聊城市东昌府区博雅学校七年级阶段练习）如图，射线BC平分∠ABD，且∠1=110°，∠2=70°．求证：AB∥CD．




【考点三 添加一条件使两条直线平行】
例题：（2022·江西赣州·七年级期中）如图，点E在AC的延长线上，若要使，则需添加条件_______（写出一种即可）


【变式训练】
1．（2022·甘肃·临泽县第三中学七年级期中）如图，填写一个能使ABCD的条件：_________．


2．（2022·吉林·公主岭市陶家中学七年级阶段练习）如图，要使，需补充一个条件，你认为这个条件应该是______（填一个条件即可）．



【考点四 平行线的性质】
例题：（2022·陕西·西安市铁一中学八年级阶段练习）如图，．，则的度数为（        ）

A．58° B．112° C．120° D．132°

【变式训练】
1．（2022·重庆市第七中学校九年级期中）如图，，，则的度数为（    ）

A．160 B．140 C．50 D．40

2．（2022·江西抚州·七年级期中）如图，直线，直线l与a，b分别相交于A，B两点，过点A作直线l的垂线交直线b与点C，若，则的度数为________．



【考点五 根据平行线的性质与判定求角度】
例题：（2021·四川省南充市高坪中学七年级阶段练习）如图，已知：，，

(1)说明：．
(2)求的度数．



【变式训练】
1．（2022·山东·宁津县德清中学七年级期中）如图，已知，，，求：

(1)
(2)的度数．




2．（2022·西藏·林芝市广东实验中学七年级期中）如图，点D，E在AC上，点F，G分别在BC，AB上，且，∠1＝∠2．

(1)求证：；
(2)若EF⊥AC，∠1＝50°，求∠ADG的度数．






【考点六 平行线的性质在生活中的应用】
例题：（2022·山东青岛·七年级期中）已知：某小区地下停车场的栏杆如图所示，当栏杆抬起到最大高度时∠ABC=150°，若此时CD平行地面AE，则_________度．


【变式训练】
1．（2022·山东·菏泽市牡丹区第二十二初级中学七年级期中）光线在不同介质中的传播速度不同，因此当光线从空气射向水中时，会发生折射．如图，在空气中平行的两条入射光线，在水中的两条折射光线也是平行的．若水面和杯底互相平行，且∠1＝132°，则∠2＝______．


2．（2022·云南昆明·七年级期末）《七彩云南》少数民族传统艺术表演，是七彩云南欢乐世界的王牌演艺节目，它荟萃云南人文之美，深受观众喜爱．在展演中，舞台上的灯光由灯带上位于点和点的两盏激光灯控制．如图，光线与灯带的夹角，当光线与灯带的夹角______时，．



【考点七 平行线的性质与判定综合应用】
例题：（2021·浙江·绍兴市锡麟中学八年级阶段练习）探究问题：已知∠ABC，画一个角∠DEF，使，且DE交BC于点P．∠ABC与∠DEF有怎样的数量关系？

(1)我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．
①图1中∠ABC与∠DEF数量关系为                    ；图2中∠ABC与∠DEF数量关系为 ；
请选择其中一种情况说明理由．
②由①得出一个真命题（用文字叙述）：              ．
(2)应用②中的真命题，解决以下问题：
若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．




【变式训练】
1．（2022·甘肃·金昌市第五中学七年级期中）如图，已知AMBN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．

(1)∠ABN的度数是 ；
(2)求∠CBD的度数；
(3)当点P运动时，∠APB与∠ADB之间的数量之比是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律．











【过关检测】
一、选择题
1．（2022·重庆市万州第二高级中学九年级期中）下列图中，不是同位角的是（    ）
A． B． C． D．
2．（2022·浙江·之江中学七年级期中）如图所示，下列说法中，错误的是（    ）

A．∠3与∠B是同旁内角 B．∠A与∠1是同位角
C．∠2与∠3是内错角 D．∠1与∠B是同位角
3．（2022·广东·深圳市宝安中学（集团）三模）如图，将直尺与角的三角尺叠放在一起，若，则∠1的大小是(   )

A． B． C． D．
4．（2022·广东·广州市第四中学七年级阶段练习）把正方形ABCD和长方形EFGH按如图的方式放置在直线l上．若∠1=43°，则∠2的度数为(   )

A． B． C． D．
5．（2022·辽宁·朝阳市第八中学七年级期中）如图，下列条件中，不能判定的是（    ）

A． B． C． D．
二、填空题
6．（2022·江苏盐城·七年级阶段练习）已知∠1=40°，则∠2=_________°时，直线a，b平行.

7．（2022·上海市罗南中学七年级阶段练习）如图，，∠A＝50°，则∠1＝_____．

8．（2022·湖北湖北·七年级期中）如图，在四边形ABCD中，点E是AB延长线上一点，请添加一个条件，使AB//CD，那么可以添加的条件是________（写出一个即可）．

9．（2022·黑龙江·哈尔滨德强学校七年级期中）如图，汽车灯的剖面图，从位于点的灯发出光照射到凹面镜上反射出的光线，都是水平线，若，，则的度数为______．

10．（2022·江西南昌·七年级期末）如图，将一副三角板按如图放置，则下列结论：①；②当时，则有；③当时，则有；④当时，则有．其中正确的序号是______．

三、解答题
11．（2022·江苏常州·七年级期末）填写下列空格：
已知：如图，点E在AB上，且CE平分∠ACD，∠1=∠2．求证：ABCD．
证明：∵CE平分∠ACD（已知），
∴____________________（__________）．
∵∠1=∠2（已知），
∴∠1=_______（___________________）．
∴ ABCD（ ______________________ ）．


12．（2022·河北·威县第三中学七年级期末）如图，已知，，求证：．

(1)请将下面证明过程补充完整．
证明：∵（已知），
∴（ ）．
又∵（已知），
∴ （等角的补角相等），
∴（ ），
∴（ ）；
(2)若平分，于点，，求的度数．

13．（2022·安徽·滁州市南谯区黄泥岗镇张浦郢中学八年级开学考试）完成下面的证明：
如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β＝90°，求证：AB∥CD．

证明：∵BE平分∠ABD （ ）
∴∠ABD＝2∠α （ ）
∵DE平分∠BDC（已知）
∵∠BDC＝ （ ）
∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β） （ ）
∵∠α+∠β＝90°（已知）
∴∠ABD+∠BDC＝（ ）
∴ AB∥CD （ ）



14．（2022·广东茂名·七年级阶段练习）如图，直线AF、DE，射线平分∠ABD交DE于点C．

(1)若∠DBF=54°，求∠2的度数；
(2)若．请说明：AB//CD．






15．（2022·黑龙江·大庆市高新区学校七年级期末）已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．

(1)填空：∠2和∠D可用关系式表示为______；∠1与∠D有怎样的关系式：______；
(2)求证：







16．（2022·河南·虞城县第二初级中学七年级期中）如图，与有公共顶点A，且点C在边BE上，CD交AE于点F且平分．，．

(1)求证：．
(2)若，求的度数．











17．（2022·山东烟台·期末）如图把一个含有30°角的直角三角板的直角顶点放在直线上，，、两点在平面上移动，请根据如下条件解答：

(1)如图1，若点在直线上，点在直线的下方，，求的度数．
(2)如图2，若点在平行直线，内部，点在直线的下方，，求的度数．


【考点一 同位角、内错角、同旁内角的辨别】
例题：（2022·全国·七年级课前预习）如图，在所标识的角中，∠1与____是同位角，∠2与_____是内错角，∠5与____是同旁内角．

【答案】     ∠4     ∠3     ∠3
【变式训练】
1．（2021·全国·七年级课时练习）如图所示，与是_________角，是直线________和直线________被直线_____所截而形成的，与是_____角，是直线________和直线___________被直线__________所截而形成的．

【答案】     内错     AB     CB     AC     同旁内     AC     BC     AB
【分析】根据三线八角中的内错角，同旁内角定义即可得出答案．
【详解】解：如图所示，与是内错角，是直线AB和直线CB被直线AC所截而形成的，
与是同旁内角，是直线AC和直线BC被直线AB所截而形成的．
故答案为内错；AB；CB；AC；同旁内；AC；BC；AB．
【点睛】本题考查三线八角中的内错角，同旁内角，掌握三线八角中的截线与被截直线，内错角与同旁内角．
2．（2022·全国·七年级）如图，

（1）∠1和∠ABC是直线AB、CE被直线________所截得的________角；
（2）∠2和∠BAC是直线CE、AB被直线________所截得的________角；
（3）∠3和∠ABC是直线________、________被直线________所截得的________角；
（4）∠ABC和∠ACD是直线________、________被直线_________所截得的________角；
（5）∠ABC和∠BCE是直线________、________被直线________所截得的________角．
【答案】     BD（BC）     同位     AC     内错     AB     AC     BC     同旁内     AB     AC     BC     同位     AB     CE     BC     同旁内
【分析】根据同位角、内错角、同旁内角的性质判断即可；
【详解】（1）∠1和∠ABC是直线AB、CE被直线BD（BC）所截得的同位角；
（2）∠2和∠BAC是直线CE、AB被直线AC所截得的内错角；
（3）∠3和∠ABC是直线AB、AC被直线BC所截得的同旁内角；
（4）∠ABC和∠ACD是直线AB、AC被直线BC所截得的同位角；
（5）∠ABC和∠BCE是直线AB、CE被直线BC所截得的同旁内角．
故答案是：BD（BC）；同位；AC；内错；AB；AC；BC；同旁内；AB；AC；BC；同位；AB；CE；BC；同旁内．
【点睛】本题主要考查了同位角、内错角、同旁内角的判断，准确分析判断是解题的关键．

【考点二 平行线的判定】
例题：（2022·山东泰安·七年级期末）如图，，，．请说明线段BE与DF的位置关系？为什么？

【答案】BEDF，见解析
【分析】由已知推出∠3+∠4=90°，利用，，得到∠1=∠4，即可得到结论BEDF．
【详解】解：BEDF，
∵，
∴∠ABC=90°，
∴∠3+∠4=90°，
∵，，
∴∠1=∠4，
∴BEDF．
【点睛】此题考查了平行线的判定定理，熟记平行线的判定定理并熟练应用是解题的关键．
【变式训练】
1．（2022·云南·弥渡县弥城镇中心学校七年级期中）已知如图所示，，点、、在同一条直线上，，且平分，试说明的理由．

【答案】见解析
【分析】根据角平分线定义求出∠1＝∠EAC，根据已知求出∠C＝∠EAC，推出∠C＝∠1，根据平行线的判定得出结论．
【详解】理由：∵AD平分∠EAC，
∴∠1＝∠EAC，
∵∠EAC＝∠B＋∠C，∠B＝∠C，
∴∠C＝∠EAC，
∴∠C＝∠1，
∴ADBC．
【点睛】本题考查了角平分线定义和平行线的判定，关键是根据定理和已知推出∠1＝∠C，题目比较典型，难度不大．
2．（2022·山东·聊城市东昌府区博雅学校七年级阶段练习）如图，射线BC平分∠ABD，且∠1=110°，∠2=70°．求证：AB∥CD．

【答案】见解析
【分析】先根据角平分线的定义和对顶角相等可得出∠ABC=∠2=70°，再由对顶角相等可得出∠1=∠BCE=110°，则∠ABC+∠BCE=180°，由此可得出结论．
【详解】证明：∵射线BC平分∠ABD，
∴∠ABC=∠2，
∵∠1=110°，∠2=70°，∠1=∠BCE，
∴∠ABC=70°，∠BCE=110°，
∴∠ABC+∠BCE=180°，
∴AB∥CD．
【点睛】本题考查的是平行线的判定，用到的知识点为：同旁内角互补，两直线平行．

【考点三 添加一条件使两条直线平行】
例题：（2022·江西赣州·七年级期中）如图，点E在AC的延长线上，若要使，则需添加条件_______（写出一种即可）

【答案】∠1=∠2 等 （写出一种即可）
【分析】根据平行线的判定定理得出直接得出即可．
【详解】解：∵当∠1 =∠2时，（内错角相等，两直线平行）；
∴若要使，则需添加条件∠1 =∠2；
故答案为：∠1=∠2．
【点睛】本题主要考查了平行线的判定，熟练掌握平行线的判定定理是解题关键．
【变式训练】
1．（2022·甘肃·临泽县第三中学七年级期中）如图，填写一个能使ABCD的条件：_________．

【答案】（答案不唯一）
【分析】根据平行线的判定定理进行解答即可．
【详解】解：填写的条件为：，
，
（内错角相等，两直线平行）．
故答案为：（答案不唯一）．
【点睛】本题考查的是平行线的判定，熟知平行线的判定定理是解答此题的关键．
2．（2022·吉林·公主岭市陶家中学七年级阶段练习）如图，要使，需补充一个条件，你认为这个条件应该是______（填一个条件即可）．

【答案】(答案不唯一）
【分析】利用两线平行的判定方法，找到一组同位角相等即可．
【详解】解：当时：，
故答案为：（答案不唯一）．
【点睛】本题考查两直线平行的判定方法．利用同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行，任选其一解题即可．

【考点四 平行线的性质】
例题：（2022·陕西·西安市铁一中学八年级阶段练习）如图，．，则的度数为（        ）

A．58° B．112° C．120° D．132°
【答案】A
【分析】根据平行线性质得出，根据对顶角相等即可得出答案．
【详解】解：如图，

∵，，
∴，
∴，故A正确．
故选：A．
【点睛】本题考查了平行线的性质和对顶角性质，解题的关键是熟练掌握：两直线平行，同位角相等．
【变式训练】
1．（2022·重庆市第七中学校九年级期中）如图，，，则的度数为（    ）

A．160 B．140 C．50 D．40
【答案】B
【分析】利用平行线的性质先求解，再利用邻补角的性质求解即可．
【详解】解：∵，，
∴，
∴，
故选B．
【点睛】本题考查的是平行线的性质，邻补角的性质，熟知两直线平行，内错角相等是解题的关键．
2．（2022·江西抚州·七年级期中）如图，直线，直线l与a，b分别相交于A，B两点，过点A作直线l的垂线交直线b与点C，若，则的度数为________．

【答案】##63度
【分析】根据，可得，即可求出的度数．
【详解】解：∵，，，
∴（两直线平行，同旁内角互补），
∴，
故答案为：．
【点睛】本题考查了平行线的性质，根据两直线平行，同旁内角互补正确找出是解答本题的关键．

【考点五 根据平行线的性质与判定求角度】
例题：（2021·四川省南充市高坪中学七年级阶段练习）如图，已知：，，

(1)说明：．
(2)求的度数．
【答案】(1)见解析
(2)
【分析】（1）根据对顶角相等得到，再利用平行线的判定即可证明；
（2）根据平行线的性质求出即可．
（1）
解：∵，，
∴，
∴；
（2）
∵，
∴，
∵，
∴．
【点睛】本题考查了平行线的性质和判定的应用，能灵活运用定理进行推理是解此题的关键．
【变式训练】
1．（2022·山东·宁津县德清中学七年级期中）如图，已知，，，求：

(1)
(2)的度数．
【答案】(1)见解析；
(2)100°．
【分析】（1）根据平行线的性质和判定方法即可得到结论；
（2）根据两直线平行，同旁内角互补，即可求解．
（1）
解：∵，
∴．
∵，
∴．
∴．
（2）
解：∵
∴．
∵，
∴
【点睛】本题主要考查平行线的判定和性质，熟练掌握两只线平行同旁内角互补是关键．
2．（2022·西藏·林芝市广东实验中学七年级期中）如图，点D，E在AC上，点F，G分别在BC，AB上，且，∠1＝∠2．

(1)求证：；
(2)若EF⊥AC，∠1＝50°，求∠ADG的度数．
【答案】(1)见解析
(2)∠ADG＝40°
【分析】（1）利用两直线平行，内错角相等，再根据同位角相等，两直线平行即可得证；
（2）先求出∠C，再根据两直线平行，同位角相等，即可得解．
（1）
证明：∵，
∴∠1＝∠DBC．
又∵∠1＝∠2，
∴∠2＝∠DBC，
∴．
（2）
∵EF⊥AC，
∴∠CEF＝90°．
∵∠2＝∠1＝50°，
∴∠C＝90°－50°＝40°．
∵，
∴∠ADG＝∠C＝40°．
【点睛】本题考查平行线的判定和性质．熟练掌握平行线的性质和判定是解题的关键．

【考点六 平行线的性质在生活中的应用】
例题：（2022·山东青岛·七年级期中）已知：某小区地下停车场的栏杆如图所示，当栏杆抬起到最大高度时∠ABC=150°，若此时CD平行地面AE，则_________度．

【答案】120
【分析】过点B作BF∥CD，因为AB⊥AE，可得∠ABF=90°，即可得出∠FBC的度数，再由BF∥CD，可得∠FBC+∠BCD=180°，代入计算即可得出答案．
【详解】解：过点B作BF∥CD，如图，

由题意可知，∠ABF=90°，
∵∠ABC=150°，
∴∠FBC=∠ABC-∠ABF=150°-90°=60°，
∵BF∥CD，
∴∠FBC+∠BCD=180°，
∴∠BCD=180°-∠FBC=180°-60°=120°．
故答案为：120．
【点睛】本题主要考查了平行线的性质，熟练应用平行线的性质进行求解是解决本题的关键．
【变式训练】
1．（2022·山东·菏泽市牡丹区第二十二初级中学七年级期中）光线在不同介质中的传播速度不同，因此当光线从空气射向水中时，会发生折射．如图，在空气中平行的两条入射光线，在水中的两条折射光线也是平行的．若水面和杯底互相平行，且∠1＝132°，则∠2＝______．

【答案】48°##48度
【分析】根据平行线的性质解答即可．
【详解】解：如图，∵水面和杯底互相平行，
∴∠1+∠3=180°，又∠1＝132°，
∴∠3=180°-∠1=48°，
∵水中的两条折射光线是平行的，
∴∠2=∠3=48°，
故答案为：48°．

【点睛】本题考查平行线的性质应用，熟练掌握平行线的性质是解答的关键．
2．（2022·云南昆明·七年级期末）《七彩云南》少数民族传统艺术表演，是七彩云南欢乐世界的王牌演艺节目，它荟萃云南人文之美，深受观众喜爱．在展演中，舞台上的灯光由灯带上位于点和点的两盏激光灯控制．如图，光线与灯带的夹角，当光线与灯带的夹角______时，．

【答案】140°或40°
【分析】当AB与在AC同侧时，CB′∥AB，同旁内角互补；当AB与CB"在AC异侧时，CB"∥AB，内错角相等．
【详解】解：如下图：

当AB与CB′在AC同侧时，
当CB′∥AB时，
∵∠CAB+∠ACB′=180°
∴∠ACB′=140°
当AB与CB"在AC异侧时，
当CB"∥AB时，
∠CAB=∠ACB"=40°
答案：140°或40°．
【点睛】本题考查了平行线的性质，解题的关键是掌握两直线平行，内错角相等，同旁内角互补及需要由分论讨论的思想求解．

【考点七 平行线的性质与判定综合应用】
例题：（2021·浙江·绍兴市锡麟中学八年级阶段练习）探究问题：已知∠ABC，画一个角∠DEF，使，且DE交BC于点P．∠ABC与∠DEF有怎样的数量关系？

(1)我们发现∠ABC与∠DEF有两种位置关系：如图1与图2所示．
①图1中∠ABC与∠DEF数量关系为                    ；图2中∠ABC与∠DEF数量关系为 ；
请选择其中一种情况说明理由．
②由①得出一个真命题（用文字叙述）：              ．
(2)应用②中的真命题，解决以下问题：
若两个角的两边互相平行，且一个角比另一个角的2倍少30°，请直接写出这两个角的度数．
【答案】(1)①∠ABC+∠DEF＝180°，∠ABC＝∠DEF，理由见解析；②如果两个角的两边互相平行，那么这两个角相等或互补
(2)30°，30°或70°和110°
【分析】（1）①根据平行线的性质，即可求解；②根据①写出结论，即可求解；
（2）设两个角分别为x和2x﹣30°，由（1）的结论可得x＝2x﹣30°或x+2x﹣30°＝180°，即可求解．
（1）
解：①如图1中，∠ABC+∠DEF＝180°．如图2中，∠ABC＝∠DEF，
故答案为：∠ABC+∠DEF＝180°，∠ABC＝∠DEF．
理由：如图1中，
∵，
∴∠DPB＝∠DEF，
∵，
∴∠ABC+∠DPB＝180°，
∴∠ABC+∠DEF＝180°．
如图2中，∵，
∴∠DPC＝∠DEF，
∵，
∴∠ABC＝∠DPC，
∴∠ABC＝∠DEF．
②结论：如果两个角的两边互相平行，那么这两个角相等或互补．
故答案为：如果两个角的两边互相平行，那么这两个角相等或互补．
（2）
解：设两个角分别为x和2x﹣30°，
由（1）得：x＝2x﹣30°或x+2x﹣30°＝180°，
解得x＝30°或x＝70°，
∴这两个角的度数为30°，30°或70°和110°．
【点睛】本题主要考查了平行线的性质，理解如果两个角的两边互相平行，那么这两个角相等或互补是解答关键．
【变式训练】
1．（2022·甘肃·金昌市第五中学七年级期中）如图，已知AMBN，∠A＝64°．点P是射线AM上一动点（与点A不重合），BC、BD分别平分∠ABP和∠PBN，分别交射线AM于点C，D．

(1)∠ABN的度数是 ；
(2)求∠CBD的度数；
(3)当点P运动时，∠APB与∠ADB之间的数量之比是否随之发生变化？若不变化，请写出它们之间的关系，并说明理由：若变化，请写出变化规律．
【答案】(1)116°
(2)58°
(3)不变，∠APB＝2∠ADB，理由见解析
【分析】（1）根据两直线平行同旁内角互补即可求解；
（2）根据角平分线的定义，结合（1）的结论即可求解；
（3）由平行线的性质可得∠APB＝∠PBN，∠ADB＝∠DBN，根据角平分线的定义可得∠PBN＝2∠DBN，即可求解．
（1）
解：∵AMBN，∠A＝64°，
∴∠ABN＝180°﹣∠A＝116°，
故答案为116°；
（2）
∵AMBN，
∴∠ABN+∠A＝180°，
∴∠ABN＝180°﹣64°＝116°，
∴∠ABP+∠PBN＝116°，
∵BC平分∠ABP，BD平分∠PBN，
∴∠ABP＝2∠CBP，∠PBN＝2∠DBP，
∴2∠CBP+2∠DBP＝116°，
∴∠CBD＝∠CBP+∠DBP＝58°；
（3）
不变，∠APB＝2∠ADB，理由如下：
∵AMBN，
∴∠APB＝∠PBN，∠ADB＝∠DBN，
∵BD平分∠PBN，
∴∠PBN＝2∠DBN，
∴∠APB＝2∠ADB．
【点睛】本题考查了平行线的性质，角平分线的定义，数形结合是解题的关键．











【过关检测】
一、选择题
1．（2022·重庆市万州第二高级中学九年级期中）下列图中，不是同位角的是（    ）
A． B． C． D．
【答案】D
【分析】根据同位角的定义（在被截线同一侧，截线的同一方位的两个角互为同位角）解决此题．
【详解】解：A．由图可知，，是同位角，故不符合题意．
B．由图可知，，是同位角，故不符合题意．
C．由图可知，，是同位角，故不符合题意．
D．由图可知，，不是同位角，故符合题意．
故选：D．
【点睛】本题主要考查同位角，解题的关键是熟练掌握同位角的定义．
2．（2022·浙江·之江中学七年级期中）如图所示，下列说法中，错误的是（    ）

A．∠3与∠B是同旁内角 B．∠A与∠1是同位角
C．∠2与∠3是内错角 D．∠1与∠B是同位角
【答案】D
【分析】根据两线被第三线所截，同旁内角，内错角和同位角的定义进行判断即可．
【详解】解：A、∠3与∠B是同旁内角，选项正确，不符合题意；
B、∠A与∠1是同位角，选项正确，不符合题意；
C、∠2与∠3是内错角，选项正确，不符合题意；
D、∠1与∠B不是同位角，选项错误，符合题意；
故选D．
【点睛】本题考查三线八角，在找角的时候，首先要确定截线，然后根据它们之间的位置关系进行确定．
3．（2022·广东·深圳市宝安中学（集团）三模）如图，将直尺与角的三角尺叠放在一起，若，则∠1的大小是(   )

A． B． C． D．
【答案】D
【分析】根据平角的定义和平行线的性质即可得到结论．
【详解】解：如图：

由题意得：，
∵ABCD，
∴∠3＝∠2＝，
∴．
故选D．
【点睛】本题考查了平行线的性质，平角的定义，熟练掌握平行线的性质是解题的关键．
4．（2022·广东·广州市第四中学七年级阶段练习）把正方形ABCD和长方形EFGH按如图的方式放置在直线l上．若∠1=43°，则∠2的度数为(   )

A． B． C． D．
【答案】B
【分析】先根据：∠1=43°，∠HEF=90°，即可得到∠CEB=47°，再根据CDAB，可得∠2=∠CEB=47°．
【详解】解：∵∠1=43°，∠HEF=90°，
∴∠CEB=47°，
∵CDAB，
∴∠2=∠CEB=47°，
故选：B．
【点睛】本题主要考查了平行线的性质，解题时注意：两直线平行，同位角相等．
5．（2022·辽宁·朝阳市第八中学七年级期中）如图，下列条件中，不能判定的是（    ）

A． B． C． D．
【答案】A
【分析】根据平行线的判定定理即可判断求解．
【详解】解：A．∠3=∠4，根据内错角相等，两直线平行可判定AD∥CB，不可判定AB∥CD，故A符合题意；
B．∠1=∠2，根据内错角相等，两直线平行可判定AB∥CD，故B不符合题意；
C．，根据同旁内角互补，两直线平行可判定AB∥CD，故C不符合题意；
D．，根据同位角相等，两直线平行可判定AB∥CD，故D不符合题意．
故选：A．
【点睛】此题考查了平行线的判定，熟记“同旁内角互补，两直线平行”、“内错角相等，两直线平行”及“同位角相等，两直线平行”是解题的关键．
二、填空题
6．（2022·江苏盐城·七年级阶段练习）已知∠1=40°，则∠2=_________°时，直线a，b平行.

【答案】40
【分析】根据平行线的性质，可以得到∠1=∠2，然后根据∠1的度数，即可得到∠2的度数．
【详解】解：∵a∥b，
∴∠1=∠2，
∵∠1=40°，
∴∠2=40°，
故答案为：40．
【点睛】本题考查平行线的性质，利用数形结合的思想解答是解答本题的关键．
7．（2022·上海市罗南中学七年级阶段练习）如图，，∠A＝50°，则∠1＝_____．

【答案】130°##130度
【分析】由平行线的性质可得出∠2，根据对顶角相得出∠1．
【详解】解：如图：

∵，
∴∠A+∠2＝180°，
∵∠A＝50°，
∴∠1＝∠2＝180°﹣∠A＝180°﹣50°＝130°．
故答案为：130°．
【点睛】本题考查了平行线的性质，解题的关键是能够根据两直线平行，同旁内角互补和对顶角相等进行分析解答．
8．（2022·湖北湖北·七年级期中）如图，在四边形ABCD中，点E是AB延长线上一点，请添加一个条件，使AB//CD，那么可以添加的条件是________（写出一个即可）．

【答案】（答案不唯一）
【分析】根据平行线的判定定理添加条件即可．
【详解】解：根据内错角相等，两直线平行，可添加或等条件，
故答案为：（答案不唯一）．
【点睛】本题考查平行线的判定，解题的关键是熟练掌握平行线的判定定理．
9．（2022·黑龙江·哈尔滨德强学校七年级期中）如图，汽车灯的剖面图，从位于点的灯发出光照射到凹面镜上反射出的光线，都是水平线，若，，则的度数为______．

【答案】##60度
【分析】如图所示，过点O作，则，根据平行线的性质求解即可．
【详解】解：如图所示，过点O作，

∵光线，都是水平线，
∴，
∴，
∴，
∴，
故答案为：．
【点睛】本题主要考查了平行线的性质，熟知两直线平行，内错角相等是解题的关键．
10．（2022·江西南昌·七年级期末）如图，将一副三角板按如图放置，则下列结论：①；②当时，则有；③当时，则有；④当时，则有．其中正确的序号是______．

【答案】②③④
【分析】根据∠CAB=∠EAD=90°及∠1=∠CAB-∠2，∠3=∠EAD-∠2，根据等量代换即可判断①；当，可得∠2和∠3的度数，利用内错角相等即可判断②；当时，可求得∠1，根据∠1=∠E内错角相等即可判断③；当时，∠3+∠D=90°即可判断④．
【详解】解：∵∠CAB=∠EAD=90°，∠1=∠CAB-∠2，∠3=∠EAD-∠2，
∴∠1=∠3，故①错误；
当，∠2=90°-∠1=45°，∠3=90°-∠2=45°，且∠B=45°，
因此∠B=∠3，
∴，故②正确；
当时，则∠1=90°-∠2=60°，且∠E=60°，
因此∠1=∠E，
∴，故③正确；
当时，则∠3+∠D=60°+30°=90°，
因此，故④正确，
故答案为：②③④．
【点睛】本题考查了三角板中角度的计算、平行线的判定及两直线垂直的判定，熟练掌握其相关判定及性质是解题的关键．
三、解答题
11．（2022·江苏常州·七年级期末）填写下列空格：
已知：如图，点E在AB上，且CE平分∠ACD，∠1=∠2．求证：ABCD．
证明：∵CE平分∠ACD（已知），
∴____________________（__________）．
∵∠1=∠2（已知），
∴∠1=_______（___________________）．
∴ ABCD（ ______________________ ）．

【答案】；角平分线定义；；等量代换；内错角相等，两直线平行
【分析】先利用角平分线定义得，从而可得出=，即可由平行线的判定定理得出结论．
【详解】解：CE平分（已知），
（  角平分线定义  ）．
（已知），
= （等量代换）．
ABCD（内错角相等，两直线平行）．
故答案为：；角平分线定义；；等量代换；内错角相等，两直线平行．
【点睛】本题考查解增分线的定义，平行线的判定，熟练掌握平行线的判定的定理是解题的关键．
12．（2022·河北·威县第三中学七年级期末）如图，已知，，求证：．

(1)请将下面证明过程补充完整．
证明：∵（已知），
∴（ ）．
又∵（已知），
∴ （等角的补角相等），
∴（ ），
∴（ ）；
(2)若平分，于点，，求的度数．
【答案】(1)两直线平行，同旁内角互补；；内错角相等，两直线平行；两直线平行，同位角相等
(2)

【分析】（1）根据平行线的性质和判断即可求解；
（2）根据垂直和平行，即可求出，且，只要求出的度数即可求出答案，根据平行线的性质，角平分线的性质即可求出，由此即可求出答案．
（1）
证明：∵（已知），
∴（两直线平行，同旁内角互补）．
又∵（已知），
∴（等角的补角相等），
∴（内错角相等，两直线平行），
∴（两直线平行，同位角相等）
故答案是：两直线平行，同旁内角互补；∠FAC=∠2；内错角相等，两直线平行；两直线平行，同位角相等．
（2）
解：∵，平分，
∴，
∵，
∴，
∴，
∵，，
∴，
∵，
∴，
故答案是：．
【点睛】本题主要考查平行线的性质和判断，以及根据平行线的性质求角的度数问题，掌握平行线的性质和判断是解题的关键．
13．（2022·安徽·滁州市南谯区黄泥岗镇张浦郢中学八年级开学考试）完成下面的证明：
如图，BE平分∠ABD，DE平分∠BDC，且∠α+∠β＝90°，求证：AB∥CD．

证明：∵BE平分∠ABD （ ）
∴∠ABD＝2∠α （ ）
∵DE平分∠BDC（已知）
∵∠BDC＝ （ ）
∴∠ABD+∠BDC＝2∠α+2∠β＝2（∠α+∠β） （ ）
∵∠α+∠β＝90°（已知）
∴∠ABD+∠BDC＝（ ）
∴ AB∥CD （ ）
【答案】已知；角平分线的定义；2∠β ；角平分线的定义；等量代换；180°；同旁内角互补两直线平行
【分析】首先根据角平分线的定义可得∠ABD=2∠α，∠BDC=2∠β，根据等量代换可得∠ABD+∠BDC=2∠α+2∠β=2（∠α+∠β），进而得到∠ABD+∠BDC=180°，然后再根据同旁内角互补两直线平行可得答案．
【详解】解：∵BE平分∠ABD （已知），
∴∠ABD=2∠α（角平分线的定义）．
∵DE平分∠BDC（已知），
∴∠BDC=2∠β （角平分线的定义），
∴∠ABD+∠BDC=2∠α+2∠β=2（∠α+∠β）（等量代换），
∵∠α+∠β=90°（已知），
∴∠ABD+∠BDC=180°，
∴AB∥CD（同旁内角互补两直线平行）．
【点睛】此题主要考查了平行线的判定，关键是掌握角平分线定义和平行线的判定方法．
14．（2022·广东茂名·七年级阶段练习）如图，直线AF、DE，射线平分∠ABD交DE于点C．

(1)若∠DBF=54°，求∠2的度数；
(2)若．请说明：AB//CD．
【答案】(1)∠2=63°
(2)见解析
【分析】（1）根据∠DBF=54°，∠ABD+∠DBF=180°，得到∠ABD=126°，根据平分得到∠2=×126°=63°；
(2)根据平分，得到，根据，得到 ，推出．
（1）
（1）∵∠DBF=54°，∠ABD+∠DBF=180°
∴∠ABD=126°
∵平分
∴∠2=×126°=63°；
（2）
(2)∵平分
∴
∵
且
∴
∴．
【点睛】本题考查了邻补角性质，角平分线性质，对顶角性质，平行线的判定定理，熟练掌握邻补角的和等于180°，角平分线把一个角分成两个相等的角，对顶角相等，同旁内角互补两直线平行，是解决此题的关键．
15．（2022·黑龙江·大庆市高新区学校七年级期末）已知：如图，∠C=∠1，∠2和∠D互余，BE⊥FD于点G．

(1)填空：∠2和∠D可用关系式表示为______；∠1与∠D有怎样的关系式：______；
(2)求证：
【答案】(1)；
(2)见解析
【分析】（1）根据互余的定义及三角形内角和定理进行求解即可；
（2）根据同角的余角相等可得，继而证明，根据内错角相等，即可得到结论．
（1）
∠2和∠D互余，
；
BE⊥FD，
，
，
；
故答案为：；；
（2）
∠2和∠D互余，
，
BE⊥FD，
，
，
，
，
，
，
．
【点睛】本题考查了余角的定义，同角的余角相等及平行线的判定，熟练掌握知识点是解题的关键．
16．（2022·河南·虞城县第二初级中学七年级期中）如图，与有公共顶点A，且点C在边BE上，CD交AE于点F且平分．，．

(1)求证：．
(2)若，求的度数．
【答案】(1)证明见解析；
(2)
【分析】（1）根据平行线的性质得出∠D=∠DCE，根据角平分线的定义得出∠ACD=∠DCE，求出∠BAC=∠ACD，根据平行线的判定得出即可；
（2）根据平行线的性质求出∠E=∠DAE，∠BAC= ∠ACD，根据角平分线的定义得出∠ACD=∠DCE，求出， 即可求出答案．
（1）
证明：∵，
∴∠D=∠DCE，
∵CD平分∠ACE，
∴∠ACD= ∠DCE，
∴∠ACD=∠D，
∵∠BAC =∠D，
∴∠BAC=∠ACD，
∴；
（2）
解：∵，
∴∠E=∠DAE，∠D =∠DCE，
∵∠DAE=∠D，
∴∠E= ∠DCE，
由（1）知，
∴∠DCE=∠B，
又∵，
∴∠E=∠B=．
【点睛】本题考查了平行线的性质和判定，角平分线的定义等知识点，能灵活运用平行线的性质和判定定理进行推理是解此题的关键．
17．（2022·山东烟台·期末）如图把一个含有30°角的直角三角板的直角顶点放在直线上，，、两点在平面上移动，请根据如下条件解答：

(1)如图1，若点在直线上，点在直线的下方，，求的度数．
(2)如图2，若点在平行直线，内部，点在直线的下方，，求的度数．
【答案】(1)
(2)

【分析】（1）先求出，再根据平行线的性质求出∠3即可解决问题；
（2）过点作，则，根据平行线的性质可得，，然后结合已知求出即可解决问题．
（1）
解：如图1，由题意可知，，，
∴，
∵，
∴，
∴；
（2）
如图2，过点作，
∵，
∴，
∴，，
∵，
∴，
∵，
∴．

【点睛】本题主要考查了平行线的性质，熟知两直线平行，内错角相等；两直线平行，同位角相等是解题的关键．