第三单元_第04课时_+解决问题-求不规则物体的容积+例7（教学课件）-六年级数学下册人教版+

这是一份第三单元_第04课时_+解决问题-求不规则物体的容积+例7（教学课件）-六年级数学下册人教版+，共27页。
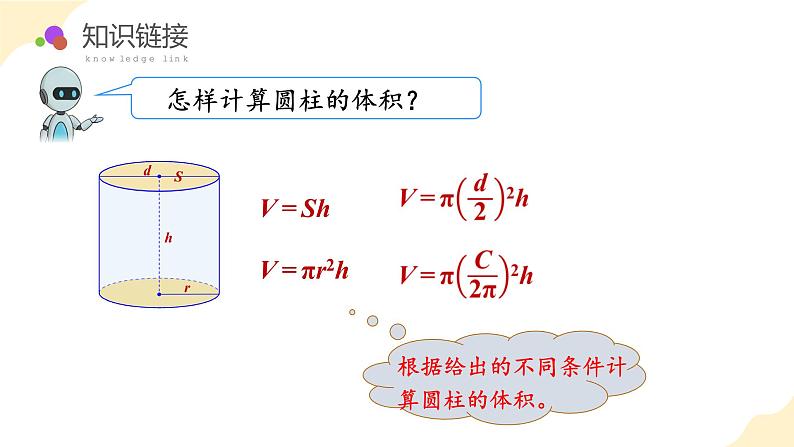
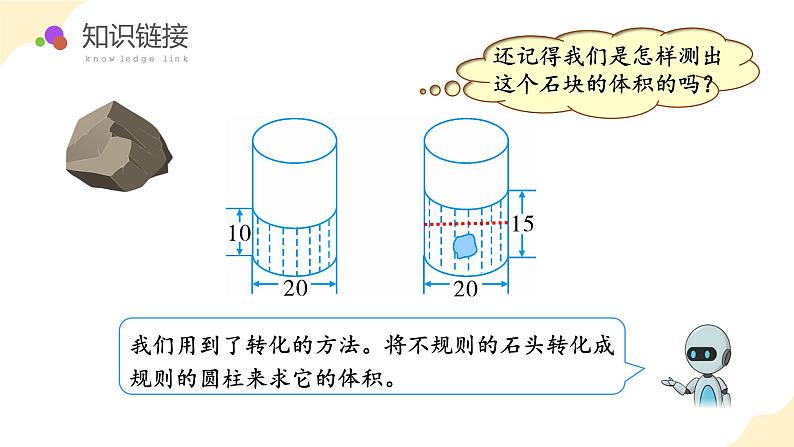
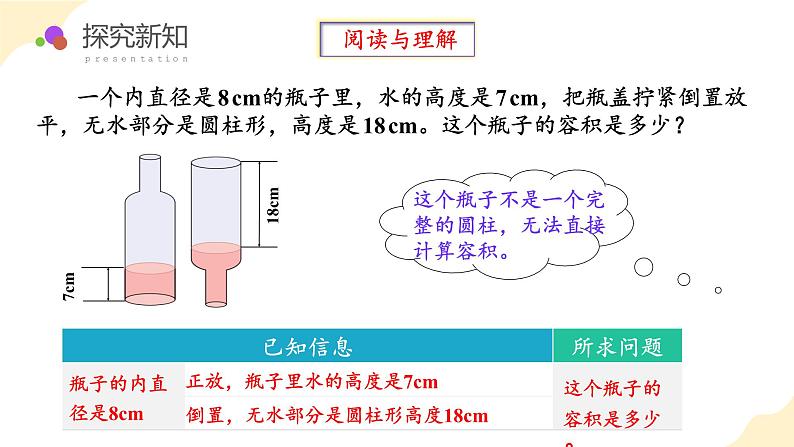
小学数学·六年级（下）·RJ第4课时 解决问题—求不规则物体的容积 例7经历探究不规则物体体积的转化、测量和计算过程，让学生在动手操作中初步建立“转化”的数学思想，体验“等积变形”的转化过程。用已学的圆柱体积知识解决生活中的实际问题，并渗透转化思想。通过情境教学及学生的亲自参与，让学生感悟数学思考的魅力和价值，进一步激发学生学习数学的热情。灵活运用圆柱的体积计算公式，体会“转化”的数学思想和策略。通过设疑、猜想、实践操作、验证的过程，完成瓶子容积的计算。让学生在动手操作中初步体会转化的数学思想，体验“等积变形”的转化过程。hdSrV=ShV=πr2h  阅读与理解，分析问题。 阅读与理解 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？瓶子的内直径是8cm正放，瓶子里水的高度是7cm倒置，无水部分是圆柱形高度18cm这个瓶子的容积是多少？ 分析与解答 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？瓶子里的水装满了吗？那该怎么求瓶子的容积呢？瓶子的容积包括几部分？ 分析与解答 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？无水部分有水部分瓶子的容积 分析与解答 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？瓶子倒置后：瓶子里的水形状变了，体积不变。瓶子里的空气形状变了，但体积不变。经过这样的“转化”，把瓶子的容积转化成一个规则的圆柱体，可以求出圆柱的体积就是瓶子的体积。运用转化法解决圆柱的容积问题。 分析与解答 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？ 分析与解答 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？方法一：答：这个瓶子的容积是1256mL。瓶子的容积=倒置前水的体积+倒置后无水部分的体积 分析与解答 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？方法二：答：这个瓶子的容积是1256mL。瓶子的容积相当于高为7+18=25(cm)的圆柱体积。 回顾与反思 一个内直径是8cm的瓶子里，水的高度是7cm，把瓶盖拧紧倒置放平，无水部分是圆柱形，高度是18cm。这个瓶子的容积是多少？达标练习，巩固成果1. 一瓶装满的矿泉水，小明喝了一些，把瓶盖拧紧后倒置放平，无水部分高10cm，内径是6cm。小明喝了多少水？ 3.14×(6÷2)2×10=282.6(cm3)=282.6(mL)答：小明喝了282.6mL水。解：2.学校要在教学区和操场之间修一道围墙，原计划用土石35m³。后来多开了一个厚度为25cm的月亮门，减少了土石的用量。现在用了多少立方米的土石？答：现在用了34.215立方米的土石。3.两个底面积相等的圆柱，一个高为4.5dm，体积是81dm。另一个高为3dm，它的体积是多少？81 ÷4.5 ×3＝18 ×3＝54（dm³ )答：它的体积是54dm³ 。4.一杯装满的奶茶，陈宇喝了一些，把瓶盖拧紧后倒置放平，空置部分高8cm，已知瓶底的内直径是6cm，陈宇喝了多少毫升？3.14×(6÷2)2×8=226.08(cm3)=226.08(mL)答：陈宇喝了226.08mL。5.下面4个图形的面积都是36dm2（图中单位：dm）。用这些图形分别卷成圆柱，哪个圆柱的体积最小？哪个圆柱的体积最大？你有什么发现？图1图2图3请你想一想，上面4个图形当以长为圆柱底面周长时，会卷成什么样的圆柱？请你动手试一试。5.下面4个图形的面积都是36dm2（图中单位：dm）。用这些图形分别卷成圆柱，哪个圆柱的体积最小？哪个圆柱的体积最大？你有什么发现？图1图2设π＝3图3图4体积：3×1.5²×4＝27（dm³）体积：3×1²×6＝18（dm³）答：图4圆柱的体积最小，图1圆柱的体积最大。我发现，左面4个图形。当以长作为圆柱底面周长时，长方形的长和宽的长度越接近，所卷成的圆柱的体积越小。6.如下图，一个底面周长为9.42厘米的圆柱体，从中间斜着截去一段后，它的体积是多少？ 3.14×(9.42÷3.14÷2)2 ×10÷2 =35.325（立方厘米）把两个相同的物体拼成一个规则的圆柱，每个图形的体积是拼成物体的一半。 答：它的体积是35.325立方厘米。根据体积不变的特性，明确瓶子正放和倒放时空余无水部分的容积是相等的，这样就把不规则的图形转化成规则的图形了，体现了转化的思想方法。用转化法解决瓶子容积问题1.瓶子容积＝水的体积＋空瓶子体积2.将不规则图形转化成规则图形。3.瓶子正放和倒置时空余部分的容积是相等的。 ★ 完成《分层作业》；★★在生活中可以做实验验证本课学习的内容。