2022-2023学年河北省石家庄市中考数学专项突破仿真模拟试题（一模二模）含解析

这是一份2022-2023学年河北省石家庄市中考数学专项突破仿真模拟试题（一模二模）含解析，共47页。试卷主要包含了选一选，填 空 题，计算题，解 答 题，综合题等内容，欢迎下载使用。
2022-2023学年河北省石家庄市中考数学专项突破仿真模拟试题（一模）
一、选一选：
1. 点A，B在数轴上的位置如图所示，其对应的数分别是a和b，对于以下结论：甲：b﹣a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：ab＞0，其中正确的是（　　）

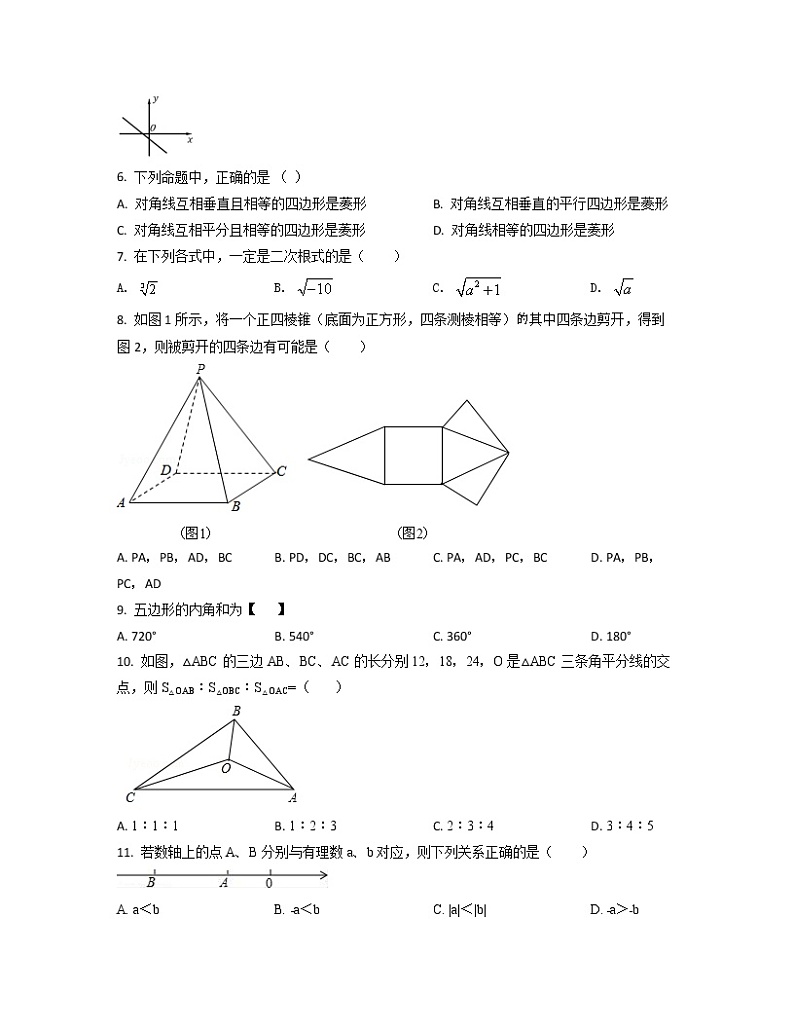
A. 甲、乙 B. 丙、丁 C. 甲、丙 D. 乙、丁
2. 下列式子中，正确的是（ ）
A. a5n÷an=a5 B. (﹣a2)3•a6=a12 C. a8n•a8n=2a8n D. (﹣m)(﹣m)4=﹣m5
3. 下列图形中，是对称但没有是轴对称图形的为（　　）
A. B.
C. D.
4. A、B两地相距180km，新修的高速公路开通后，在A、B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为
A. B.
C. D.
5. 在直角坐标系中，既是正比例函数y=kx，又是y值随x的增大而减小的图象是（　　）
A. B. C. D.
6. 下列命题中，正确的是 （   ）
A. 对角线互相垂直且相等的四边形是菱形 B. 对角线互相垂直的平行四边形是菱形
C. 对角线互相平分且相等的四边形是菱形 D. 对角线相等的四边形是菱形
7. 在下列各式中，一定是二次根式的是（　　）
A. B. C. D.
8. 如图1所示，将一个正四棱锥（底面为正方形，四条测棱相等）其中四条边剪开，得到图2，则被剪开的四条边有可能是（　　）

A. PA，PB，AD，BC B. PD，DC，BC，AB C. PA，AD，PC，BC D. PA，PB，PC，AD
9. 五边形的内角和为【 】
A. 720° B. 540° C. 360° D. 180°
10. 如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S△OAB：S△OBC：S△OAC=（　　）

A. 1：1：1 B. 1：2：3 C. 2：3：4 D. 3：4：5
11. 若数轴上的点A、B分别与有理数a、b对应，则下列关系正确的是（　　）

A. a＜b B. ﹣a＜b C. |a|＜|b| D. ﹣a＞﹣b
12. 已知A、C两地相距40千米，B、C两地相距50千米，甲乙两车分别从A、B两地同时出发到C地．若乙车每小时比甲车多行驶12千米，则两车同时到达C地．设乙车的速度为x千米/小时，依题意列方程正确的是（　　）
A. B. C. D.
13. 已知一直角三角形的木版，三边的平方和为1800，则斜边长为 （ ）
A. 80 B. 30 C. 90 D. 120
14. 已知一元二次方程x2﹣3x﹣3=0的两根为α与β，则的值为（　　）
A. ﹣1 B. 1 C. ﹣2 D. 2
15. 如图，在中，点、、分别在边、、上，且，，若，则的值为（ ）

A B. C. D.
16. 已知抛物线y=x2-（2m+1）x+2m没有第三象限，且当x＞2时，函数值y随x增大而增大，则实数m的取值范围是（　　）
A. 0≤m≤1.5 B. m≥1.5 C. 0≤m≤1 D. 0＜m≤1.5
二、填 空 题：
17. 4的平方根是 ．
18. 分解因式：_________．
19. 如图，矩形ABCD中，AD=2，AB=5，P为CD边上的动点，当△ADP与△BCP相似时，DP=__．

三、计算题：
20. 计算：﹣12016﹣[2﹣（﹣1）2016]÷（﹣）× ．
21. 计算：
四、解 答 题：
22. 已知：如图，，，.求证.

23. 如图,△ABC中,AD平分∠BAC,EG∥AD,找出图中的等腰三角形,并给出证明．

24. 将九年级部分男生掷实心球的成绩进行整理，分成5个小组（x表示成绩，单位：米）．A组：5.25≤x＜6.25；B组：6.25≤x＜7.25；C组：7.25≤x＜8.25；D组：8.25≤x＜9.25；E组：9.25≤x＜10.25，并绘制出扇形统计图和频数分布直方图（没有完整）．规定x≥6.25为合格，x≥9.25为．
（1）这部分男生有多少人？其中成绩合格的有多少人？
（2）这部分男生成绩中位数落在哪一组？扇形统计图中D组对应的圆心角是多少度？
（3）要从成绩的学生中，随机选出2人介绍，已知甲、乙两位同学的成绩均为，求他俩至少有1人被选中的概率．

25. 某产品生产车间有工人10名.已知每名工人每天可生产甲种产品12个或乙种产品10个,且每生产一个甲种产品可获得利润100元,每生产一个乙种产品可获得利润180元.在这10名工人中,车间每天安排x名工人生产甲种产品,其余工人生产乙种产品．
（1）请写出此车间每天获取利润y（元）与x（人）之间的函数关系式；
（2）若要使此车间每天获取利润为14400元,要派多少名工人去生产甲种产品？
（3）若要使此车间每天获取利润没有低于15600元,你认为至少要派多少名工人去生产乙种产品才合适？
26. 为方便市民通行，某广场计划对坡角为30°，坡长为60 米的斜坡AB进行改造，在斜坡中点D 处挖去部分坡体（阴影表示），修建一个平行于水平线CA 的平台DE 和一条新的斜坡BE．

（1）若修建的斜坡BE 的坡角为36°，则平台DE的长约为多少米？
（2）在距离坡角A点27米远的G处是商场主楼，小明在D点测得主楼顶部H 的仰角为30°，那么主楼GH高约为多少米？
（结果取整数，参考数据：sin 36°＝0．6，cos 36°＝0．8，tan 36°＝0．7，＝1．7）
五、综合题：
27. 如图，顶点为P（4，－4）的二次函数图象原点（0，0），点A在该图象上，
OA交其对称轴于点M，点M、N关于点P对称，连接AN、ON
（1）求该二次函数的关系式.
（2）若点A的坐标是（6，－3），求△ANO的面积.
（3）当点A在对称轴右侧的二次函数图象上运动，请解答下列问题：
①证明：∠ANM=∠ONM
②△ANO能否为直角三角形？如果能，请求出所有符合条件的点A的坐标，如果没有能，请说明理由.


















2022-2023学年河北省石家庄市中考数学专项突破仿真模拟试题（一模）
一、选一选：
1. 点A，B在数轴上的位置如图所示，其对应的数分别是a和b，对于以下结论：甲：b﹣a＜0；乙：a+b＞0；丙：|a|＜|b|；丁：ab＞0，其中正确的是（　　）

A. 甲、乙 B. 丙、丁 C. 甲、丙 D. 乙、丁
【正确答案】C

【详解】试题解析: 甲正确.
乙错误.
丙正确.
丁错误.
故选C.
2. 下列式子中，正确的是（ ）
A. a5n÷an=a5 B. (﹣a2)3•a6=a12 C. a8n•a8n=2a8n D. (﹣m)(﹣m)4=﹣m5
【正确答案】D

【详解】试题解析：A. a5n÷an=a5 ，错误；
B. (﹣a2)3•a6=a12，错误；
C. a8n•a8n=2a8n，错误；
D. (﹣m)(﹣m)4=﹣m5，正确.
故选D.
3. 下列图形中，是对称但没有是轴对称图形的为（　　）
A. B.
C. D.
【正确答案】C

【分析】根据轴对称图形及对称图形的定义，所给图形进行判断即可．
【详解】A、既没有是轴对称图形，也没有是对称图形，故本选项错误；
B、是轴对称图形，也是对称图形，故本选项错误；
C、没有是轴对称图形，是对称图形，故本选项正确；
D、是轴对称图形，没有是对称图形，故本选项错误.
故选C．
4. A、B两地相距180km，新修的高速公路开通后，在A、B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h．若设原来的平均车速为xkm/h，则根据题意可列方程为
A. B.
C. D.
【正确答案】A

【分析】直接利用在A，B两地间行驶的长途客车平均车速提高了50%，而从A地到B地的时间缩短了1h，利用时间差值得出等式即可．
【详解】解：设原来的平均车速为xkm/h，则根据题意可列方程为：
﹣=1．
故选A．
本题主要考查了由实际问题抽象出分式方程，根据题意得出正确等量关系是解题的关键．
5. 在直角坐标系中，既是正比例函数y=kx，又是y的值随x的增大而减小的图象是（　　）
A. B. C. D.
【正确答案】C

【分析】根据正比例函数图象的性质进行解答．
【详解】根据正比例函数的图象必过原点，排除A，D；
B、从左到右呈上升趋势，没有符合题意；
C、又要y随x的增大而减小，则k＜0，从左向右看，图象是下降的趋势．
故选C．
本题考查了正比例函数图象，了解正比例函数图象的性质：它是原点的一条直线．当k＞0时，图象一、三象限，y随x的增大而增大；当k＜0时，图象二、四象限，y随x的增大而减小．
6. 下列命题中，正确的是 （   ）
A. 对角线互相垂直且相等的四边形是菱形 B. 对角线互相垂直的平行四边形是菱形
C. 对角线互相平分且相等的四边形是菱形 D. 对角线相等的四边形是菱形
【正确答案】B

【分析】根据菱形的判定方法依次分析各选项即可．
【详解】A．对角线互相垂直且相等的四边形没有一定是菱形，故本选项错误；
B．对角线互相垂直的平行四边形是菱形，故本选项正确．
C．对角线互相平分且相等的四边形是矩形，故本选项错误；
D．对角线相等的四边形没有一定是菱形，故本选项错误．
故选： B．
本题本题考查了真命题，属于基础应用题，只需学生熟练掌握菱形的判定方法，即可完成．
7. 在下列各式中，一定是二次根式的是（　　）
A. B. C. D.
【正确答案】C

【详解】试题解析：：A、是三次根式；故本选项错误；
B、被开方数-10＜0，没有是二次根式；故本选项错误；
C、被开方数a2+1≥0，符合二次根式的定义；故本选项正确；
D、被开方数a＜0时，没有是二次根式；故本选项错误；
故选C．
点睛：式子（a≥0）叫做二次根式，特别注意a≥0，a是一个非负数．
8. 如图1所示，将一个正四棱锥（底面为正方形，四条测棱相等）的其中四条边剪开，得到图2，则被剪开的四条边有可能是（　　）

A. PA，PB，AD，BC B. PD，DC，BC，AB C. PA，AD，PC，BC D. PA，PB，PC，AD
【正确答案】A

【详解】由棱锥的展开特点知，被剪开的四条边有可能是PA，PB，AD，BC.
故选A.
9. 五边形的内角和为【 】
A. 720° B. 540° C. 360° D. 180°
【正确答案】B

【详解】根据多边形内角和定理，五边形的内角和为：（5－2）×180°=540°．故选B．
10. 如图，△ABC的三边AB、BC、AC的长分别12，18，24，O是△ABC三条角平分线的交点，则S△OAB：S△OBC：S△OAC=（　　）

A. 1：1：1 B. 1：2：3 C. 2：3：4 D. 3：4：5
【正确答案】C

【分析】直接根据角平分线的性质即可得出结论．
【详解】∵O是△ABC三条角平分线的交点，AB、BC、AC的长分别12，18，24，∴S△OAB：S△OBC：S△OAC=AB：OB：AC=12：18：24=2：3：4．
故选C．
本题考查了角平分线的性质，熟知角的平分线上的点到角的两边的距离相等是解答此题的关键．
11. 若数轴上的点A、B分别与有理数a、b对应，则下列关系正确的是（　　）

A. a＜b B. ﹣a＜b C. |a|＜|b| D. ﹣a＞﹣b
【正确答案】C

【详解】根据数轴特征∵b