湖南省长沙市2023届高三数学上学期新高考适应性考试试卷（Word版附解析）

长沙市2023年新高考适应性考试

数学

一、选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．

1. 已知复数z满足，则（    ）

A.  B.

C. 2 D.

【答案】B

【详解】，

所以.

故选：B

2. 设集合，，则的元素个数是（    ）

A. 1 B. 2

C. 3 D. 4

【答案】C

【详解】联立，即，解得：或，

即，

故的元素个数为3.

故选：C

3. 已知，，，则（    ）

A.  B.

C.  D.

【答案】C

【详解】，

所以，所以.

，所以.

所以有.

故选：C.

4. 的展开式中，常数项为（    ）

A.  B.

C.  D.

【答案】D

【详解】展开式的通项公式为，

所以的展开式中，常数项为

，

故选：D

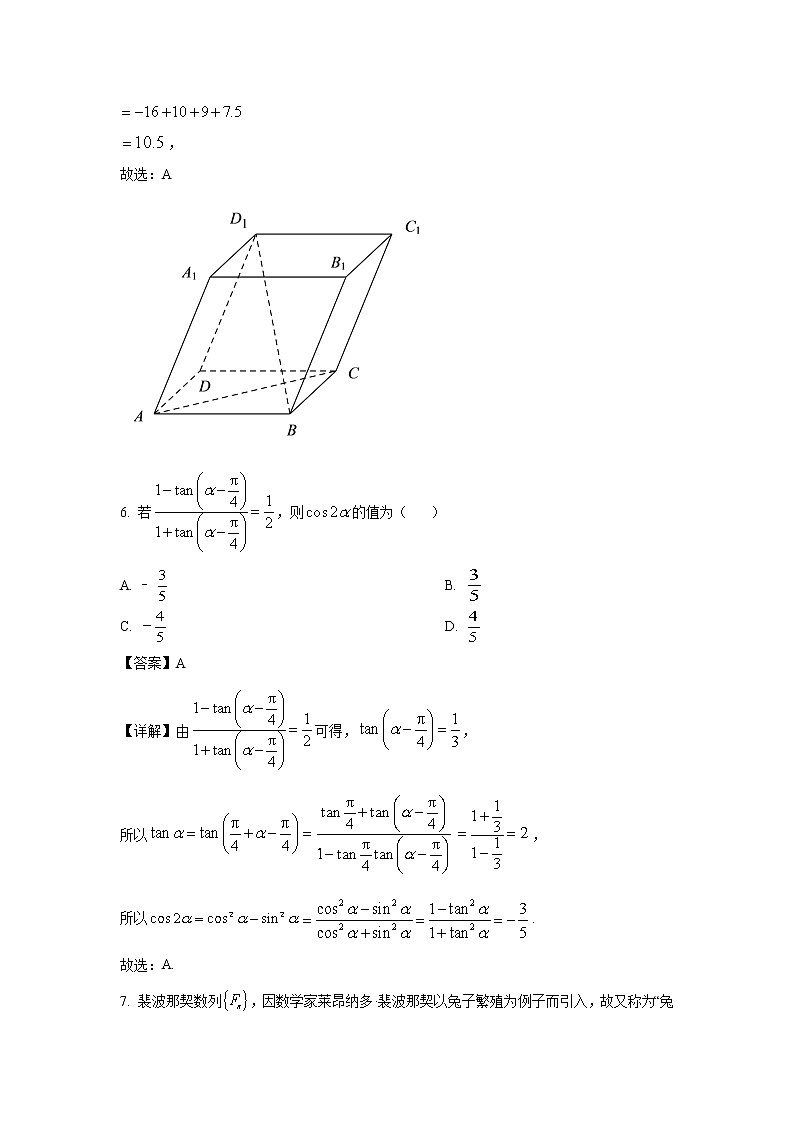
5. 在平行六面体中，已知，，，，，则的值为（    ）

A. 10.5 B. 12.5

C. 22.5 D. 42.5

【答案】A

【详解】由题意得，，

因为，，，，，

所以

，

故选：A

6. 若，则的值为（    ）

A.  B.

C.  D.

【答案】A

【详解】由可得，，

所以，

所以.

故选：A.

7. 裴波那契数列，因数学家莱昂纳多·裴波那契以兔子繁殖为例子而引入，故又称为“兔子数列”，该数列满足，且．卢卡斯数列是以数学家爱德华·卢卡斯命名，与裴波那契数列联系紧密，即，且，则（    ）

A.  B.

C.  D.

【答案】C

【详解】因为，

所以当时，，

所以，

故，

因为，

所以，，

故，

所以.

故选：C.

8. 在平面直角坐标系中,已知,,若该平面中存在点,同时满足两个条件与,则的取值范围是（    ）

A.  B.

C.  D.

【答案】C

【详解】解:由题知,不妨设,

因为,

所以,

化简可得: ,

故点在以为圆心,为半径的圆上,

又因为,

所以,

化简可得:,

即点在以为圆心,为半径的圆上,

故只需圆与圆有交点即可,

即,

同时平方化简可得: ,

即,

解得: .

故选:C

二、选择题：本题共4小题，每小题5分，共20分.在每小题给出的四个选项中，有多项符合题目要求，全部选对的得5分，部分选对的得2分，有选错的得0分．

9. 已知双曲线的方程为，则（    ）

A. 渐近线方程为 B. 焦距为

C. 离心率为 D. 焦点到渐近线的距离为8

【答案】BC

【详解】焦点在轴上，故渐近线方程为，A错误；

，故，故焦距为，B正确；

离心率为，C正确；

焦点坐标为，故焦点到渐近线的距离为，D错误.

故选：BC

10. 自然环境中，大气压受到各种因素的影响，如温度、湿度、风速和海拔等方面的改变，都将导致大气压发生相应的变化，其中以海拔的影响最为显著．下图是根据一组观测数据得到海拔6千米～15千米的大气压强散点图，根据一元线性回归模型得到经验回归方程为，决定系数为；根据非线性回归模型得到经验回归方程为，决定系数为 ，则下列说法正确的是（    ）

A. 由散点图可知，大气压强与海拔高度负相关

B. 由方程可知，海拔每升高1千米，大气压强必定降低4.0kPa

C. 由方程可知，样本点的残差为

D. 对比两个回归模型，结合实际情况，方程的预报效果更好

【答案】ACD

【详解】对于A项，由图象知，海拔高度越高，大气压强越低，所以大气压强与海拔高度负相关，故A项正确；

对于B项，回归直线得到的数据为估计值，而非精确值，故B项错误；

对于C项，当时，，又由散点图知观测值为，所以样本点的残差为，故C项正确；

对于D项，随着海拔高度的增加，大气压强越来越小，但不可能为负数，因此方程的预报效果更好，故D项正确.

故选：ACD.

11. 已知函数与相交于A，B两点，与相交于C，D两点，若A，B，C，D四点的横坐标分别为，，，，且，，则（    ）

A.  B.

C.  D.

【答案】ABD

【详解】由题意可知是方程 的一个根，则，将 代入得，所以也是方程的一个根，所以，故，故A正确，

由题意可知是方程 的一个根，则，则，所以也是方程的一个根，所以，故，故B正确，

设点在函数上，则满足，即点关于直线的对称点为，将代入得，即可，因此可知在函数上， 即关于直线的对称，又 关于直线的对称，因此可知对称，对称，

故 和，

所以 ，，故D正确，

由于 ，故C错误，

故选：ABD

12. 如图，已知是边长为4的等边三角形，D，E分别是AB，AC的中点，将沿着DE翻折，使点A到点P处，得到四棱锥，则（    ）

A. 翻折过程中，该四棱锥的体积有最大值为3

B. 存某个点位置，满足平面平面

C. 当时，直线与平面所成角的正弦值为

D. 当时，该四棱锥的五个顶点所在球的表面积为

【答案】ACD

【详解】

如图1，设，分别是，的中点.则，，，且.

对于A项，当平面平面时，四棱锥的体积最大. 的高为，四边形为高为的梯形，梯形面积，体积，故A项正确；

对于B项，设平面平面，则，有，，可得平面，即为平面与平面所成的二面角，由可知，，故B项错误；

对于C项，如图1，过点作，垂足为.由B分析可得，平面，所以平面平面，平面平面，平面，所以平面.所以即为直线与平面所成的角.由题意可知，，，，在中，由余弦定理可得，所以；在中，，所以直线与平面所成角的正弦值为；

对于D项，当时，由，可知，即，又，且，则平面，又平面，则平面平面.四棱锥的外接球球心为，的外心为，则平面.如图2，易知点为等腰梯形的外心，则平面，

则四边形为矩形，且，从而有，从而该四棱锥的五个顶点所在球的表面积为，故D项正确.

故选：ACD.

三、填空题：本题共4小题，每小题5分，共20分．

13. 已知，，，若，则________．

【答案】

【详解】因为已知，，，

所以，

又因为，

所以，解得.

故答案为：

14. 已知函数,若函数的图象关于点中心对称,且关于直线轴对称,则的最小值为______．

【答案】3

【详解】解:由题知的图象关于点中心对称,

且关于直线轴对称,

则与之间的距离为,

即,,

即,,
 

因为,

所以当时,的最小值为3.

故答案为:3

15. 已知O为坐标原点，F为抛物线的焦点，过点F作倾斜角为60°的直线与抛物线交于A，B两点（其中点A在第一象限）．若直线AO与抛物线的准线l交于点D，设，的面积分别为，，则______．

【答案】##0.5625

【详解】

由题意知，，直线方程为.设，.

联立直线方程与抛物线的方程，解得或.

因为点A在第一象限，所以，，

直线方程为，点坐标为.

因为，所以轴.

所以，

，

所以.

故答案为：.

16. 已知函数，若关于x的方程恰有两个不相等的实数根，且，则的取值范围是______．

【答案】

【详解】函数在上单调递增，，在上单调递增，，

当，即时，，且，

当，即时，，且，

当，即时，，且，

因此，在坐标系内作出函数的图象，如图，

再作出直线，则方程有两个不等实根，当且仅当直线与函数的图象有两个不同交点，

观察图象知方程有两个不等实根，当且仅当，

此时，且，即，且，则有，

令，求导得，令，

当时，，即函数在上单调递增，

当时，，即，因此函数在上单调递增，

，而，于是当时，，有，

所以的取值范围是.

故答案为：

四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．

17. 已知数列为等差数列，数列为等比数列，满足，，．

（1）求数列，的通项公式；

（2）求数列的前n项和．

【答案】（1），；   

（2）.

小问1详解】

解：设的公差为，的公比为，，，

联立，整理可得，解得，

所以，.

【小问2详解】

解：由（1）知，

则，①

，②

①-②，得

.

所以.

18. 在锐角中，角A，B，C所对应的边分别为a，b，c，已知．

（1）求角B的值；

（2）若，求的周长的取值范围．

【答案】（1）   

（2）

【小问1详解】

，由正弦定理得：，

即，

由余弦定理得：，

因为，

所以；

【小问2详解】

锐角中，，，

由正弦定理得：，

故，

则

，

因为锐角中，，

则，，

解得：，

故，，

则，

故，

所以三角形周长的取值范围是.

19. 如图，在以A，B，C，D，E，F为顶点的六面体中（其中平面EDC），四边形ABCD是正方形，平面ABCD，，且平面平面 ．

（1）设 为棱 的中点，证明：四点共面；

（2）若，求平面与平面的夹角的余弦值．

【答案】（1）见解析    （2）

【解析】

【小问1详解】

连接,由于四边形ABCD是正方形，所以,

又平面，平面,所以 ,

平面，所以平面，

由于为棱中点，，所以 ,

又平面平面，平面平面，平面,

所以平面 ,

因此,所以四点共面，

【小问2详解】

由于两两垂直，故建立如图所示的空间直角坐标系，

,,设，

由（1）知,故，解得，故,

,

设平面，的法向量分别为则

即，取，则 ，

即，取，则 ，

设平面与平面的夹角为，则

20. 为了调动大家积极学习党的二十大精神，某市举办了党史知识的竞赛．初赛采用“两轮制”方式进行，要求每个单位派出两个小组，且每个小组都要参加两轮比赛，两轮比赛都通过的小组才具备参与决赛的资格．某单位派出甲、乙两个小组参赛，在初赛中，若甲小组通过第一轮与第二轮比赛的概率分别是，，乙小组通过第一轮与第二轮比赛的概率分别是，，且各个小组所有轮次比赛的结果互不影响.

（1）若该单位获得决赛资格的小组个数为X，求X的数学期望；

（2）已知甲、乙两个小组都获得了决赛资格，决赛以抢答题形式进行．假设这两组在决赛中对每个问题回答正确的概率恰好是各自获得决赛资格的概率．若最后一道题被该单位的某小组抢到，且甲、乙两个小组抢到该题的可能性分别是45%，55%，该题如果被答对，计算恰好是甲小组答对的概率．

【答案】（1）见解析    （2）

【小问1详解】

设甲乙通过两轮制的初赛分别为事件则

由题意可得，的取值有

则的分布列为：

所以

【小问2详解】

设甲乙两组对每个问题回答正确的概率分别为，两组在决赛中对每个问题回答正确的概率恰好是各自获得决赛资格的概率，

则一个题被甲小组抢到为事件，则，

设一个题答对为事件，则

该题如果被答对，恰好是甲小组答对即为

21. 设A，B是椭圆上异于的两点，且直线AB经过坐标原点，直线PA，PB分别交直线于C，D两点．

（1）求证：直线PA，AB，PB的斜率成等差数列；

（2）求面积的最小值．

【答案】（1）证明过程见解析   

（2）

【小问1详解】

设，则，，

直线的斜率，直线的斜率为，直线的斜率为，

，

故直线PA，AB，PB的斜率成等差数列；

小问2详解】

直线PA的方程为，与联立得：

，

同理可得：直线PB的方程为，与联立得：

，

故，

因为，设，

故，

其中，

故当时，取得最小值，最小值为，

又点到直线的距离，

故面积的最小值为.

22. 已知函数，其中．

（1）求的最大值；

（2）若不等式对于任意的恒成立，求实数a的取值范围．

【答案】（1）1    （2）

【小问1详解】

，，

令，解得：或，

令，解得：，

故在，上单调递增，在上单调递减，

故在处取得极大值，，

令，即当时，恒成立，

故在处取得最大值，；

【小问2详解】

设，其中，

①当时，，符合题意，

②当时，，且，

由（1）知：在单调递增，故，

若，，则单调递减，有，符合题意，

若，，符合题意，

若，即时，，则在上单调递减，有，符合题意，

若，即时，存在使得，

当时，，故，则单调递增，可得，不合题意，

因此当时，满足题意得，

③当时，，且，

由②可知：只需考虑，

若，即时，由（1）知在上单调递减，故，

存在，使得，

当时，，得，则单调递减，

可得：，不合题意，

若，即时，由（1）可知：当时，，，

故，则在上单调递增，有，符合题意，

若，，符合题意，

若，下面证明符合题意，

当时，，故，

当时，设，则，

可得在上单调递增，在上单调递减，

故，

从而，符合题意，

综上：.