人教版七年级下册5.4 平移测试题

这是一份人教版七年级下册5.4 平移测试题，文件包含专题17坐标系中的面积和平移有关解析版docx、专题17坐标系中的面积和平移有关原卷版docx等2份试卷配套教学资源，其中试卷共28页， 欢迎下载使用。


专题17 坐标系中的面积（和平移有关）
最基础最核心
1．在平面直角坐标系中，三角形的三个顶点的位置如图，为三角形内一点，的坐标为
（1）平移三角形，使点与原点重合，请画出平移后的三角形
（2）直接写出的对应点的坐标；并写出平移的规律.
（ ， ）；
（ ， ）；
（ ， ）；
（3）求三角形的面积.

【答案】（1）画见解析；（2）；（3）
【分析】
（1）点C平移到原点，即点C向左平移1个单位，向下平移两个单位，按同样的方法平移点A、B即可；
（2）由图中坐标系即可写出平移后点的坐标，易得平移规律；
（3）用A、B、C三点所在的长方形的面积减去三个直角三角形的面积即可.
【详解】
（1）如图所示：

（2）∵点的对应点的坐标为，∴平移规律是:先向左平移1个单位长度，再向下平移2个单位长度，
∴
（3）如图所示

所以三角形的面积为
【点睛】
本题考查了平面直角坐标系，涉及了图形的平移、点的坐标、割补法求面积，比较容易，熟练掌握图形的平移方法及求网格中不规则图形面积的方法是解题的关键.
2．如图所示的平面直角坐标系中，A(4，3)，B(3，1)，C(1，2)，将三角形ABC平移后得到三角形DEF，已知B点平移后的对应点E(0，－3)(A点与D点对应，C点与F点对应)．
(1)画出平移后的三角形DEF，并写出点D的坐标为 ，点F的坐标为 ；
(2)求三角形ABC的面积．

【答案】（1）图详见解析，（1，-1），（-2，-2）；（2）
【分析】
（1）画出图象即可解决问题；
（2）将所在的图形补充为一个矩形，然后利用矩形的面积减去周边的面积即可解决问题；
【详解】
解：（1）如图所示，， ，，
故答案为，；

(2)S三角形ABC＝2×3－×1×3－×1×2－×1×2
＝6－－1－1
＝．
【点睛】
本题考查作图平移变换，三角形的面积等知识，解题的关键是灵活运用所学知识解决问题．
3．如图，在平面直角坐标系中，已知点A（-2，5），B（-3,3），C（1，2），点P（m,n）是三角形ABC内任意一点，三角形经过平移后得到三角形A1B1C1，点P的对应点为P1（m+6,n-2）．
（1）直接写出平移后点A1、B1、C1的坐标分别为 ．
（2）画出三角形ABC平移后的三角形A1B1C1．．

【答案】（1）(4，3)（3,1）（7，0）;（2）见解析.
【分析】
（1）利用点P和点为P1坐标特征确定平移的方向与距离，然后根据此平移规律可确定点B1的坐标；
（2）利用（1）中的平移规律确定A1、B1、C1，然后描点依次连接即可.
【详解】
（1）由点P（m,n）的对应点为P1（m+6,n-2）可得：A1（-2+6，5-2）=(4，3)，B1（-3+6,3-2）=（3,1），C1（1+6，2-2）=（7，0）；
（2）由（1）将A1、B1、C1三点标在坐标轴上，再依次连接，如图，△A1B1C1为所作：

【点睛】
本题考查作图−平移变换，解题的关键是确定平移后图形的基本要素有两个：平移方向、平移距离，作图时要先找到图形的关键点．
4．在如图所示的平面直角坐标系中，将三角形ABC平移后得到三角形A'B'C'，它们的各个顶点坐标如下表所示．
三角形ABC
A（a，0）
B（3，0）
C（5，5）
三角形A'B'C'
A'（4，2）
B'（7，b）
C'（c，d）
（1）观察表中各对应点坐标的变化，并填空：三角形ABC先向　 　平移　 　个单位长度，再向　 　平移　 　个单位长度可以得到三角形A'B'C'．
（2）在平面直角坐标系中画出三角形ABC及平移后的三角形A'B'C'．
（3）求出三角形A'B'C'的面积．

【答案】（1）右，4，上，2；（2）见详解；（3）
【分析】
（1）利用已知点坐标进而分析得出对应点平移规律，进而得出答案；
（2）利用平移的性质结合对应点坐标得出答案；
（3）直接利用三角形面积求法得出答案．
【详解】
解：（1）∵B（3，0），B’（7，b）
∴对应点向右平移了4个单位长度，
∵A（a，0），A'（4，2），
∴对应点向上平移了2个单位长度，
∴三角形ABC先向右平移4个单位长度，再向上平移2个单位长度可以得到三角形A'B'C'，
故答案是：右，4，上，2；
（2）由（1）可知：A（0，0），B'（7，2），C'（9，7），
如图所示：△ABC和△A'B'C'即为所求；

（3）S三角形A'B'C'＝S三角形ABC＝×3×5＝．
【点睛】
此题主要考查了平移的性质以及三角形面积求法，正确得出对应点坐标是解题关键．
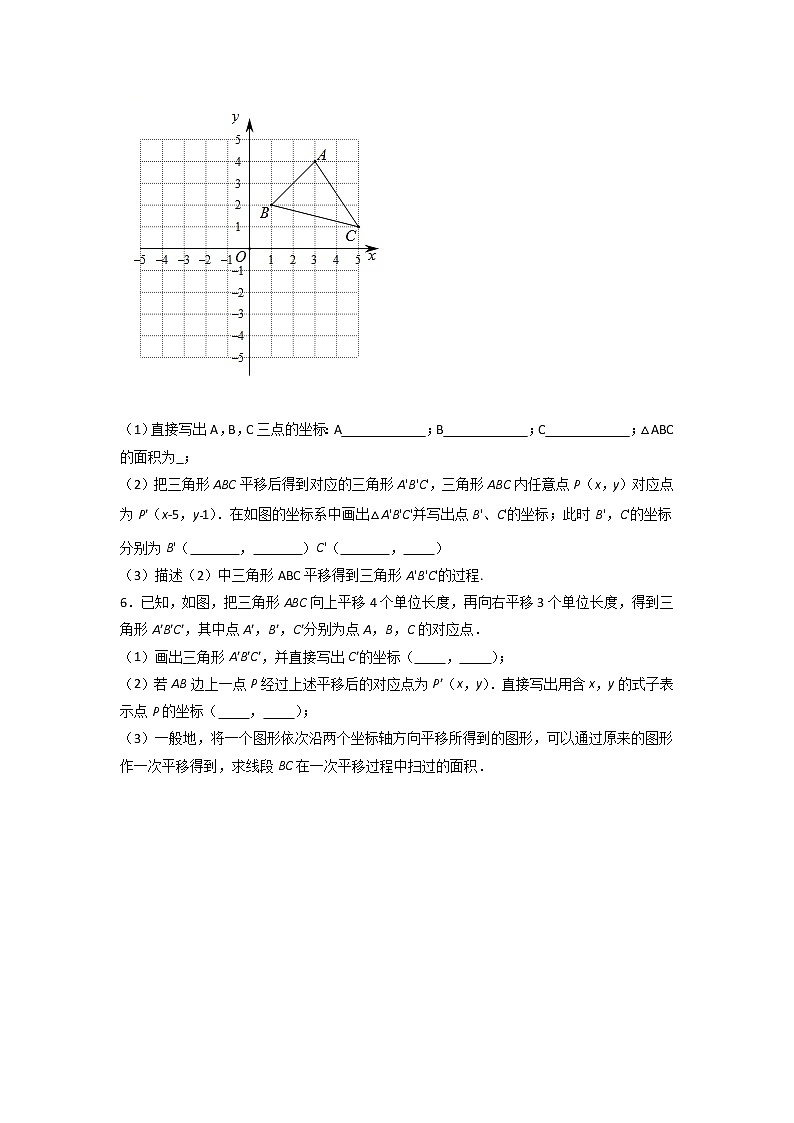
5．下面的方格图是由边长为1的小正方形拼成的，△ABC的顶点A，B，C均在小正方形的顶点上.在图中建立如图所示的平面直角坐标系，回答下列问题：


（1）直接写出A，B，C三点的坐标：A ；B ；C ；△ABC的面积为 ；
（2）把三角形ABC平移后得到对应的三角形A'B'C'，三角形ABC内任意点P（x，y）对应点为P′（x-5，y﹣1）．在如图的坐标系中画出△A'B'C'并写出点B'、C'的坐标；此时B'，C'的坐标分别为B'（　 　，　 　）C'（　 　，　 　）
（3）描述（2）中三角形ABC平移得到三角形A'B'C'的过程.
【答案】（1）；（2）作图见解析；B'（　-4　，　1　）C'（　0 　，　0 　）；（3）三角形ABC先向左平移5个单位长度，再向下平移1个单位长度得到三角形A'B'C'.
【分析】
（1）根据平面直角坐标系写出各个点的坐标即可，△ABC的面积可用长方形的面积减去三个直角三角形的面积即可得；
（2）根据点P的坐标变化可得，将三角形先向左平移5个单位，再向下平移1个单位，作出图形即可，此时、的坐标可得；
（3）根据点P的坐标变化可得，将三角形先向左平移5个单位，再向下平移1个单位．
【详解】
（1）根据平面直角坐标系可得：A （3,4） ；B （1,2） ；C （5,1） ；
如下图所示：= - - -
=
=5


△ABC的面积为 5 ；
故答案为：；
（2）作图如下图所示：


点B'、C'的坐标为：B'（　-4　，　1　）C'（　0 　，　0 　）；
（3）平移的过程：三角形ABC先向左平移5个单位长度，再向下平移1个单位长度
得到三角形A'B'C'．
【点睛】
本题主要考查了平面直角坐标系中的坐标与面积的运算，熟练掌握平面直角坐标系中的平移规律是解题的关键．
6．已知，如图，把三角形ABC向上平移4个单位长度，再向右平移3个单位长度，得到三角形A′B′C′，其中点A′，B′，C′分别为点A，B，C的对应点．
（1）画出三角形A′B′C′，并直接写出C′的坐标（　 　，　 　）；
（2）若AB边上一点P经过上述平移后的对应点为P′（x，y）．直接写出用含x，y的式子表示点P的坐标（　 　，　 　）；
（3）一般地，将一个图形依次沿两个坐标轴方向平移所得到的图形，可以通过原来的图形作一次平移得到，求线段BC在一次平移过程中扫过的面积．

【答案】（1）作图见解析；4，2；（2）x﹣3，y﹣4；（3）16．
【分析】
（1）利用平移变换的性质分别作出A，B，C的对应点A′，B′，C′即可；
（2）根据平移变换的规律解决问题即可；
（3）利用平行四边形的面积公式计算即可．
【详解】
解：（1）如图，△A′B′C′即为所求作．

点C′的坐标是(4，2)．
故答案为：4，2；
（2）点P可以看作由P′（x，y）向下平移4个单位长度，再向左平移3个单位长度得到的，∴P(x﹣3，y﹣4)，
故答案为：x﹣3，y﹣4；
（3）由平移的性质可知线段BC在一次平移过程中扫过的区域是平行四边形，
∴线段BC在一次平移过程中扫过的面积＝4×4＝16．
【点睛】
本题考查坐标与图形的平移变换，平行四边形的面积等知识，解题的关键是正确作出图形，属于中考常考题型．
越战越勇技能提升
7．如图，在平面直角坐标系中，三角形ABC的顶点坐标分别为，，，把三角形ABC进行平移，平移后得到三角形，且三角形ABC内任意点平移后的对应点为．
（1）画出平移后的图形；
（2）三角形ABC是经过怎样平移后得到三角形的？写出三个顶点，，的坐标；
（3）求三角形ABC的面积．

【答案】（1）见解析；（2），，；（3）．
【分析】
（1）由将ABC内任意点平移后的对应点为知三角形ABC向右平移3个单位长度，再向下平移4个单位长度；即可画出图形，
（2）由平移后的对应点为知三角形ABC向右平移3个单位长度，再向下平移4个单位长度，根据直角坐标系即可写出平移后的顶点坐标，
（3）根据割补法即可求解面积.
【详解】
（1）如图所示：

（2）三角形ABC向右平移3个单位长度，再向下平移4个单位长度；，，；
（3）三角形ABC的面积为5×5-=．
【点睛】
此题主要考查直角坐标系的平移，解题的关键是熟知平移的性质及直角坐标系的坐标表示.
8．如图，在正方形网格中，每个小正方形的边长均为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为（﹣4，5）、（﹣1，3）．
（1）请在如图所示的网格平面内画出平面直角坐标系；
（2）点p（m，n）是△ABC边BC上任意一点，三角形经过平移后得到△A1B1C1，点P的对应点为p（m＋6，n﹣2）．
①直接写出点B的坐标 　 　；
②画出△ABC平移后的△A1B1C1；
（3）在y轴上是否存在点P，使△AOP的面积等于△ABC面积，若存在，请求出点P的坐标：若不存在，请说明理由．

【答案】（1）见解析；（2）①(4，-1)；②见解析；（3）存在，或
【分析】
（1）根据A或C坐标确定原点后可以画出平面直角坐标系；
（2）由题意可以写出B点坐标，然后由P点的坐标变化可以得到平移方式，从而可以得到B点对应点坐标并画出△A1B1C1；
（3）根据题意可以得到关于OP的方程，解方程得到OP的值后即可写出P点坐标．
【详解】
（1）解：∵C坐标为（-1，3），
∴根据坐标的确定方法，C向右平移1格，然后向下平移3格即得原点O位置，
∴以O为原点，经过O且水平向右为x轴正方向，经过O且竖直向上为 y轴正方向即可建立平面直角坐标系如图所示：

（2）由题意可得P-P'的平移方式为：沿x轴向右平移6个单位，同时沿y轴向下平移2个单位，
∵B点为（-2，1），
∴ ①B点对应点坐标为（-2+6，1-2）即(4，-1)，
故答案为（4，-1）；
②解：分别把A、B、C沿x轴向右平移6个单位的同时沿y轴向下平移2个单位，即可得到A1、B1、C1，顺次连接A1、B1、C1即可得到如图所示的△A1B1C1；

（3）解：∵，
∴
∴，
∴当点P在O点上方时： ；
当点P在O点下方时：
【点睛】
本题考查平面直角坐标系中的平移和三角形面积应用，熟练掌握平面直角坐标系的建立、平移的坐标变化及其作图、坐标系中三角形面积的计算及应用等是解题关键．
9．在平面直角坐标系中，三角形ABC的位置如图．把三角形ABC平移后，三角形ABC内任意点P（x，y）的对应点为P′（x+2，y﹣3）．

（1）画出平移后的图形；
（2）三角形ABC是经过怎样平移后得到三角形A′B′C′？
（3）若在x正半轴存在一点P，使得△PAB的面积是△ABC面积的2倍，则P点坐标是　　．
【答案】（1）见解析；（2）见解析；（3）（，0）
【分析】
（1）根据点P的对应点P′的坐标得出平移方向和距离，据此作出三顶点平移后的对应点，顺次连接可得；
（2）由（1）可知；
（3）先根据待定系数法求出AB的函数解析式，确定与x轴的交点坐标，再根据待定系数法找到经过C点的与AB平行的函数解析式，确定与x轴的交点坐标，再根据两点间的距离公式，可求P点坐标．
【详解】
解：（1）如图所示，△A′B′C′即为所求；

（2）由题意知，△ABC先向右平移2个单位、再向下平移3个单位可以得到△A′B′C；
（3）设直线AB的函数解析式为y＝kx+b，依题意有
，
解得．
故直线AB的函数解析式为y＝4x+7，
当y＝0时，4x+7＝0，解得x＝﹣，
故直线AB与x轴的交点坐标为（﹣，0）；
设经过C点的与AB平行的函数解析式y＝4x+b1，依题意有
4×1+b1＝2，
解得b1＝﹣2，
故经过C点的与AB平行的函数解析式y＝4x﹣2，
当y＝0时，4x﹣2＝0，解得x＝，
故经过C点与AB平行的直线与x轴的交点坐标为（，0）；
[﹣（﹣）]×2＝，
﹣﹣＝﹣（不合题意舍去），
﹣+＝．
故P点坐标是（，0）
故答案为：（，0）．
【点睛】
本题考查的是作图-平移变换，熟知图形平移不变性的性质是解答此题的关键．
10．如图，三角形ABC的顶点A在原点，B，C坐标分别为B(3，0)，C(2，2)，将三角形ABC向左平移1个单位后再向下平移2个单位，可得到三角形．
（1）请画出平移后的三角形的图形．
（2）写出三角形各个顶点的坐标．
（3）在x轴上是否存在点P，使三角形ACP的面积等于三角形ABC面积的一半，若存在，请直接写出点P的坐标；若不存在，请说明理由．

【答案】（1）见解析；（2），，；（3）存在，P1(，0)，P2(﹣，0)
【分析】
（1）根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置，然后顺次连接即可；
（2）根据平面直角坐标系写出各点的坐标即可；
（3）设点P（x，0），则OP＝|x|，由S△ACP＝S△ABC建立关于x的方程，解之可得点P的坐标．
【详解】
解：（1）如图所示：

（2）A'（﹣1，﹣2），B'（2，﹣2），C'（1，0）；
（3）设P（x，0），则OP＝|x|，
∵三角形ACP的面积等于三角形ABC面积的一半，
∴OP×2＝AB×2，
∴|x|×2＝3×2，
解得x＝±，
∴P1（，0），P2（﹣，0）．
【点睛】
本题考查了利用平移变换作图，三角形的面积．熟练掌握平移的性质，准确找出对应点是解题的关键．
11．如图，在正方形网格中，每个小正方形的边长均为1，格点三角形（顶点是网格线的交点的三角形）ABC的顶点A、C的坐标分别为、．

（1）请在如图所示的网格平面内画出平面直角坐标系；
（2）点是边BC上任意一点，三角形经过平移后得到，点P的对应点为．
①直接写出点的坐标 ；
②画出平移后的．
（3）在y轴上是否存在点P，使的面积等于面积的，若存在，请求出点P的坐标；若不存在，请说明理由．
【答案】（1）见解析；（2）①；②见解析；（3）存在，或．
【分析】
（1）根据A、C的坐标分别为、先确定原点O，即可画图；
（2）①根据的对应点确定平移方向和距离，即可求解；
②根据平移的方向和距离确定A、B、C的对应点，然后连线即可；
（3）再网格图中利用割补法先求得的面积，然后根据题意即可求解．
【详解】

解：（1）如图所示；
（2）①∵，
∴先向右平移6格，再向下平移2格，得到
∵
∴，
故答案是：(4，-1)；
②如图所示；
（3）
∴
∴
当点P在O点上方时：；
当点P在O点下方时：．
【点睛】
此题主要考查平移的性质，正确理解平移中，点的坐标变化特点是解题关键．
乘风破浪拓展冲刺
12．如图，在平面直角坐标系中，点A（0，a）、C（b，0）满足+|b﹣2|＝0．
（1）求点A、点C的坐标；
（2）已知坐标轴上有两动点P、Q同时出发，P点从C点出发向左以1单位长度每秒的速度匀速移动，Q点从O点出发以2个单位长度每秒的速度向上移动，点D（1，2）是线段AC上一点，设运动时间为t（t＞0）秒，当S△ODQ＝2S△ODP时，此时是否存在点M（m，6），使得S△ODM＝3S△ODQ，若存在，求出点M的坐标；若不存在，请说明理由；
（3）点F是线段AC上一点，满足∠FOC＝∠FCO，点G是第二象限中一点，连接OG，使得∠AOG＝∠AOF，点E是线段OA上一动点，连接CE交OF于点H，当点E在线段OA上运动的过程中，直接写出的值．

【答案】（1）A（0，4），C（2，0）；（2）存在，M（7，6）、M（-1，6）、M（15，6）或M（-9，6）；（3）2．
【分析】
（1）根据非负性求得a、b值即可；
（2）分两种情形当点P在线段OC上时；当点P在线段CO延长线上时，分别构建方程求出点P坐标，根据S△ODM＝3S△ODQ，再次分别构建方程即可解决问题；
（3）过H点作AC的平行线，交x轴于P，先判定OG∥AC，再根据角的和差关系以及平行线的性质，得出∠PHO=∠GOF=∠1+∠2，∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4，最后代入进行计算即可．
【详解】
（1）∵+|b﹣2|＝0
∴a-2b=0，b-2=0．
求得：a=4，b=2，
∴A（0，4），C（2，0）．
故答案为A（0，4），C（2，0）．
（2）当点P在线段OC上时，由题意：
，解得t=．
当点P在CO的延长线上时，由题意：
，解得t=4．
故当t=或4时，S△ODQ＝2S△ODP．

如图，当点P在线段OC上时，P（，0），Q（0，），
∵S△ODM=3S△ODQ，
∴，
或者
解得：m=7，m=-1
∴M（7，6）或M（-1，6）．

如图，当点P在CO的延长线上时，P（-2，0），Q（0，8），
此时，，
或者
解得：m=-9，m=15
∴M（-9，6）或M（15，6）．
综上所述：存在点M（7，6）、M（-1，6）、M（15，6）或M（-9，6）使得条件成立．
（3）

∵∠2+∠3=90°，
又∵∠1=∠2，∠3=∠FCO，
∴∠GOC+∠ACO=180°，
∴OG∥AC，
∴∠1=∠CAO，
∴∠OEC=∠CAO+∠4=∠1+∠4，
如图，过H点作AC的平行线，交x轴于P，则∠4=∠PHC，PH∥OG，
∴∠PHO=∠GOF=∠1+∠2，
∴∠OHC=∠OHP+∠PHC=∠GOF+∠4=∠1+∠2+∠4，
∴．
故答案为：=2．
【点睛】
本题考查三角形的综合，涉及坐标与图形性质、非负性的性质、三角形的面积公式、平行线的性质，解答的关键是学会添加常用添加辅助线，学会用转化的思想解决问题，属于中考压轴题.