沪科版九年级数学总复习二次函数中动点图形的面积最值课件

这是一份沪科版九年级数学总复习二次函数中动点图形的面积最值课件，共26页。PPT课件主要包含了学前准备，激趣定标，自主学习，法宝一，我的收获，自我检测等内容，欢迎下载使用。
二次函数中动点图形的面积问题
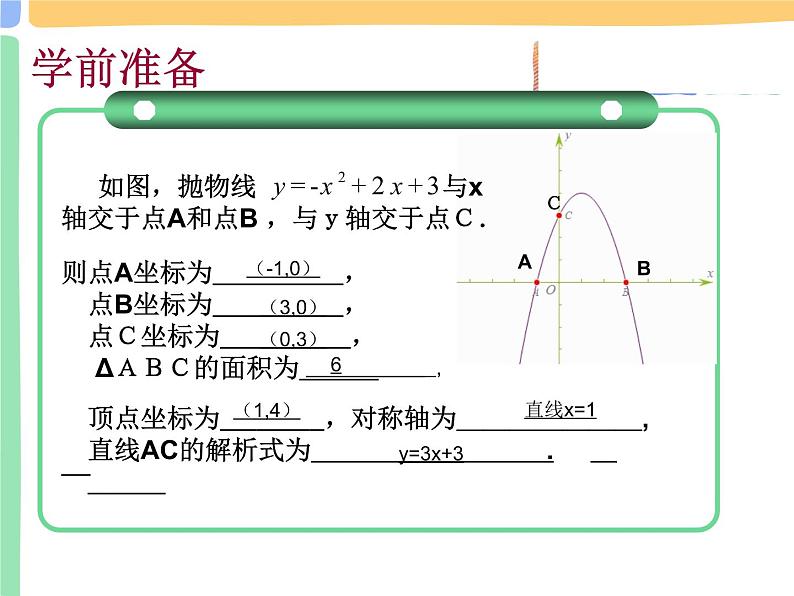
如图，抛物线　　　　　　　与x轴交于点A和点B ，与ｙ轴交于点Ｃ．　　　　　　　　　　　　
则点A坐标为 　　　 ，　点B坐标为 　　　 ，　点Ｃ坐标为 　　　 ， 　ΔＡＢＣ的面积为　　　
顶点坐标为 　　 ，对称轴为＿＿＿＿＿＿＿,直线AC的解析式为 .　　 　
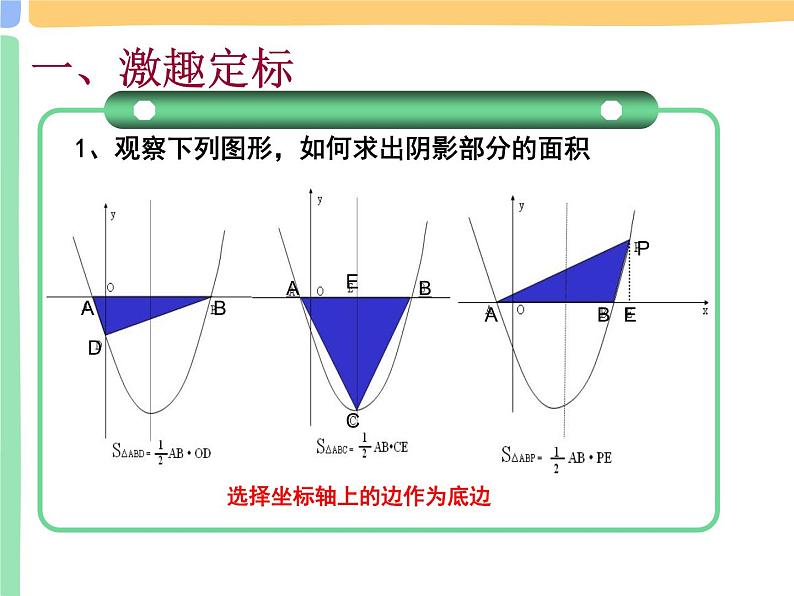
1、观察下列图形，如何求出阴影部分的面积
选择坐标轴上的边作为底边
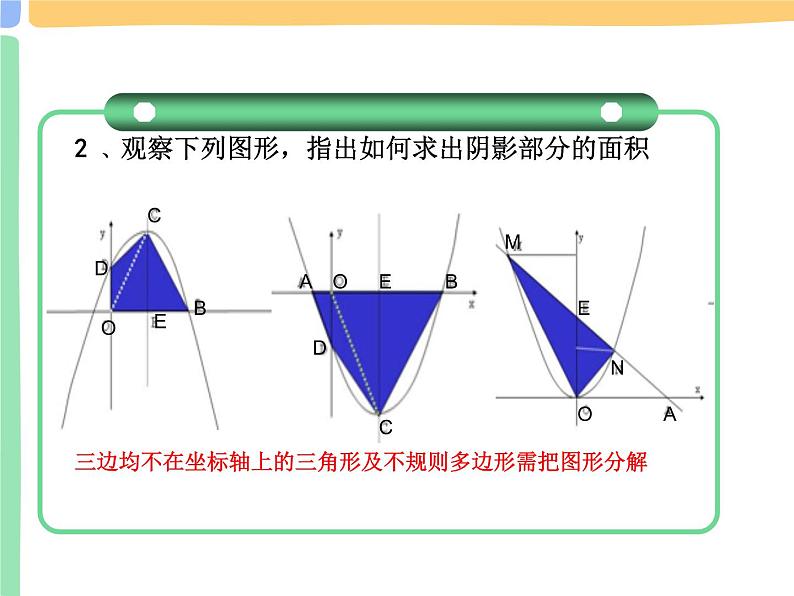
2 、观察下列图形，指出如何求出阴影部分的面积
三边均不在坐标轴上的三角形及不规则多边形需把图形分解
能够根据二次函数中不同图形的特点选择合适的方法解答图形的面积。掌握利用二次函数的解析式求出相关点的坐标，从而得出相关线段的长度，利用水平宽和铅垂高方法求图形面积。
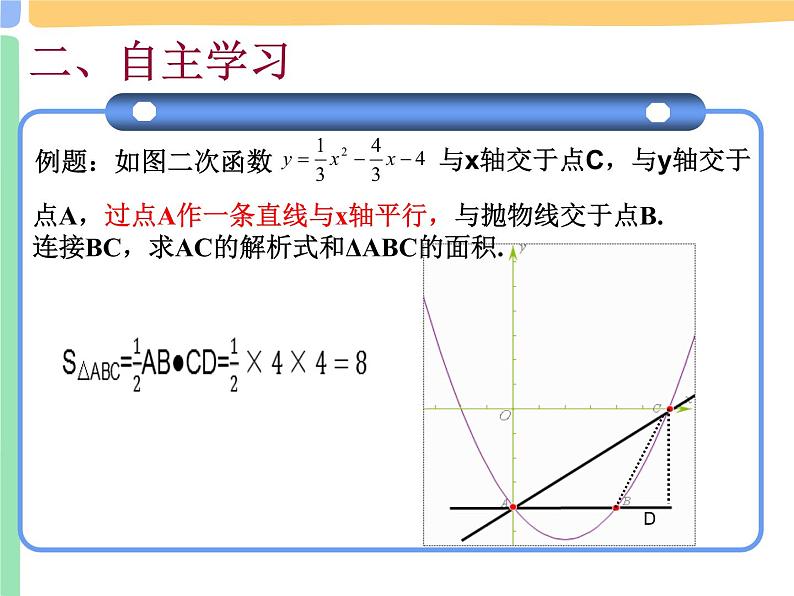
点A，过点A作一条直线与x轴平行，与抛物线交于点B.连接BC，求AC的解析式和ΔABC的面积.
与x轴交于点C，与y轴交于
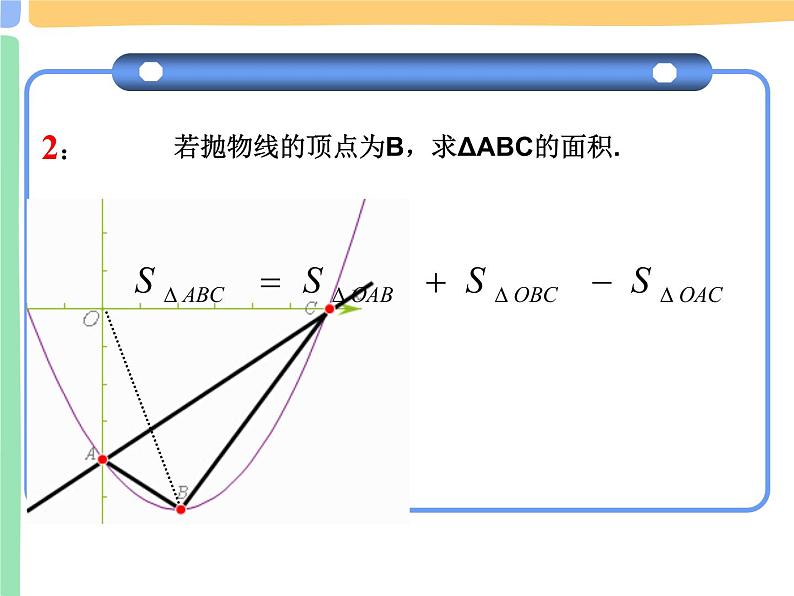
若抛物线的顶点为B，求ΔABC的面积.
【分析】显然对于这样一个位置的三角形，面积公式并不太好用，割补倒是可以一试，比如这样：
构造矩形ADEF，用矩形面积减去三个三角形面积即可得△ABC面积．
此处AE+AF即为A、B两点之间的水平距离．
这是在“补”，同样可以采用“割”：
由题意得：AE+BF=6．
根据A、B两点坐标求得直线AB解析式为：
由点C坐标（4,7）可得D点横坐标为4，从而得到D点纵坐标为2，最后得到CD=7-2=5
【方法总结】作以下定义：A、B两点之间的水平距离称为“水平宽”；过点C作x轴的垂线与AB交点为D，线段CD即为AB边的“铅垂高”．如图可得：
【解题步骤】（1）求A、B两点水平距离，即水平宽；（2）过点C作x轴垂线与AB交于点D，可得点D横坐标同点C；（3）求直线AB解析式并代入点D横坐标，得点D纵坐标；（4）根据C、D坐标求得铅垂高；（5）利用公式求得三角形面积．
所谓“一母式”，就是用一个字母表示动点坐标。多个动点就可以用多个一母式。
E(m, )
P(n, )
若A（-2,3），B（-4,3），则AB=————。若A（2,3），B（2,-5），则AB=————。
变式1：若B、C是抛物线与x轴的交点，A是抛物线与y轴的交点，点D是线段AC上的动点，过点D作x轴的垂线与抛物线相交于点E，当点D运动到什么位置时，线段DE最长。
由例题可知：点A（0，-4），点C（6,0）直线AC：
若点B是线段AC下方的抛物线上的动点，那么，ΔABC的面积有最大值吗？如果有，请求出最大面积和此时点B的坐标.
若点B是线段AC下方的抛物线 上的动点，如果三角形ABC有最大面积，请求出最大面积和此时点B的坐标；如果没有，请说明理由.
若B、C是抛物线与x轴的交点，A是抛物线与y轴的交点，点D是线段AC上的动点，过点D作x轴的垂线与抛物线相交于点E，四边形ABCE的面积最大值吗 ？如果有,求此时点E的坐标.
变式4：如图，抛物线中的点A、B、C与例题中的点A、B、C一样，点P是直线AC上方抛物线上的动点，是否存在点P，使
，若存在，求出点P的坐标，若不存在，说明理由.
五思想 三法宝思路1：以静制动 法宝一：两点公式思路2：构建模型 法宝二：一母式思路3：分类思想 法宝三：铅垂高思路4：方程思想思路5：检验思想
用含x的代数式表示相关线段的长度
与y轴交于点C，直线y=x+1与抛物线交于E，F两点．点Ｐ是直线EF下方抛物线上的动点，求△PEF
面积的最大值及点P的坐标.
与x轴交于A(-3,0)，B(1,0)两点，