2022-2023学年广东省深圳市福田外国语高级中学高一上学期期中数学试卷

2022-2023学年广东省深圳市福田外国语高级中学高一（上）

期中数学试卷

一、单选题（本大题共8小题，共40.0分。在每小题列出的选项中，选出符合题目的一项）

1.    若集合，集合，则图中阴影部分表示(    )

A.
B.
C.
D.

2.    若，则下列不等式正确的是(    )

A.  B.  C.  D.

3.    设，，，则，，的大小关系(    )

A.  B.  C.  D.

4.    若“”是“”的充分不必要条件，则实数的取值不可以是(    )

A. B. C. D.

5.    已知函数，若，则实数(    )

A.  B. C. D.

6.    下列函数是偶函数且在上单调递增的函数是(    )

A.  B.  C.  D.

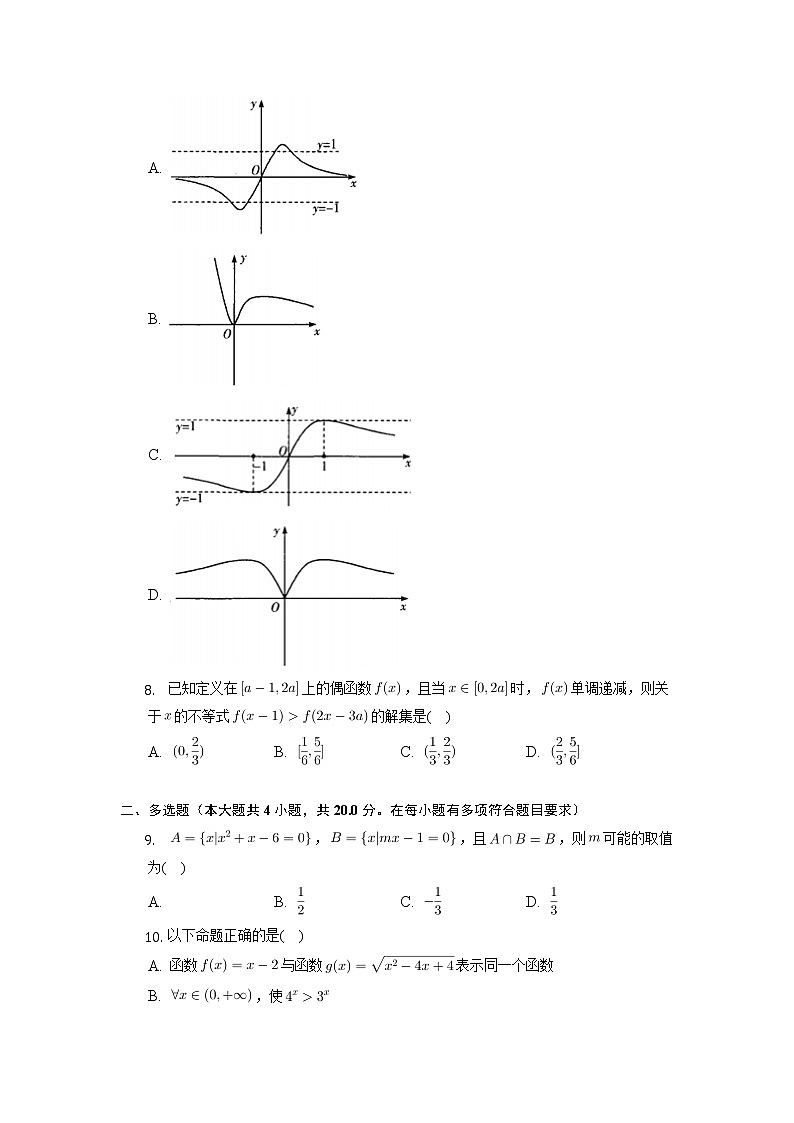
7.    函数的部分图象大致为(    )

A.
B.
C.
D.

8.    已知定义在上的偶函数，且当时，单调递减，则关于的不等式的解集是(    )

A.  B.  C.  D.

二、多选题（本大题共4小题，共20.0分。在每小题有多项符合题目要求）

9.    ，，且，则可能的取值为(    )

A. B.  C.  D.

10. 以下命题正确的是(    )

A. 函数与函数表示同一个函数
B. ，使
C. 若，且，则的最小值为
D. 若函数的定义域为，则函数的定义域为

11. 已知关于的不等式的解集为，则(    )

A.
B. 不等式的解集为
C.
D. 不等式的解集为

12. 德国著名数学家狄利克雷在数学领域成就显著．世纪，狄利克雷定义了一个“奇怪的函数”其中为实数集，为有理数集．则关于函数有如下四个命题，其中真命题的是(    )

A. 函数是偶函数
B. ，，恒成立
C. 任取一个不为零的有理数，对任意的恒成立
D. 不存在三个点，，，使得为等腰直角三角形

三、填空题（本大题共4小题，共20.0分）

13. 命题：，，则为          ．
14. 已知幂函数在上单调递增，则______．
15. 若函数是奇函数，且在定义域上是减函数，，不等式的解集是______．
16. 已知函数满足，且，有，则实数的取值范围是______．

四、解答题（本大题共6小题，共70.0分。解答应写出文字说明，证明过程或演算步骤）

17. 本小题分
    已知集合，．
    若，求；
    若，求的取值范围．
18. 本小题分
    已知函数，且此函数图象过点．Ⅰ求实数的值；Ⅱ判断函数的奇偶性并证明；Ⅲ讨论函数在上的单调性，并证明你的结论．
19. 本小题分
    已知函数是定义在上的奇函数，当时，．
    求的值；
    求函数的解析式；
    把函数图象补充完整，并写出函数的单调区间．

20. 本小题分
    已知函数为偶函数．
    求实数的值；
    当时，若函数的值域为，求，的值．
21. 本小题分
    第四届中国国际进口博览会于年月日至日在上海举行．本届进博会有多项新产品、新技术、新服务．某跨国公司带来了高端空调模型参展，通过展会调研，中国甲企业计划在年与该跨国公司合资生产此款空调．生产此款空调预计全年需投入固定成本万元，生产千台空调，需另投入资金万元，且经测算，当生产千台空调时需另投入的资金万元．现每台空调售价为万元时，当年内生产的空调当年能全部销售完．
    求年该企业年利润万元关于年产量千台的函数关系式；
    年产量为多少时，该企业所获年利润最大？最大年利润为多少？注：利润销售额成本．
22. 本小题分
    已知函数．
    若存在实数，使得成立，试求的最小值；
    若对任意的，，都有恒成立，试求的取值范围．
    

答案和解析

1.【答案】 

【解析】解：集合，集合，
阴影部分所表示的集合为；
故选：．
 

2.【答案】 

【解析】解：，不妨令，，
则，故A错误，无意义，，故D错误，
，C正确．
故选C．
3.【答案】 

【解析】

解：函数为减函数；
故，
函数在上为增函数；
故，
故，
故选：．

4.【答案】 

【解析】解：解不等式得，或，
“”是“”的充分不必要条件，
或，
，
实数的取值不可以是．
故选：．
 

5.【答案】 

【解析】解：函数，当时，由，
可得实数．
当时，由，可得．
综上，可得，
故选：．
6.【答案】 

【解析】解：对于，为偶函数，当时，在递减，故A错误；
对于，的定义域为，，则为奇函数，故B错误；
对于，为偶函数，且时，为增函数，故C正确；
对于，的定义域为，当时，为减函数，故D错误．
故选：．
7.【答案】 

【解析】解：，定义域为，
所以，
所以为奇函数，排除选项B和，
当时，，当且仅当，即时，等号成立，
所以的最大值为，即选项A错误．
故选：．
 

8.【答案】 

【解析】解：是偶函数，则，得，即函数的定义域为，
当时，单调递减，
则不等式等价为不等式，
则，平方得，
得，得或，
又，得，得，，
即不等式的解集为，
故选：．
9.【答案】 

【解析】解：，
，，
时，，满足；
时，，又，
或，
或．
综上，实数的值可以为或或．
故选：．
 

10.【答案】 

【解析】解：对于选项A，
，
，
故与不是同一个函数，
故错误；
对于选项B，
由幂函数的单调性知，
，
在是增函数，
，即，
故正确；
对于选项C，

，
当且仅当，即，时，等号成立；
故的最小值为；
故正确；
对于选项D，
函数的定义域为，
，
解得，
故函数的定义域为；
故错误；
故选：．
 

11.【答案】 

【解析】解：关于的不等式的解集为，
，
即，；
故选项A错误；
不等式可化为，
故不等式的解集为，
故选项B正确；
，
故选项C正确；
，
，
即，
的解集为，
故选项D错误；
故选：．
12.【答案】 

【解析】

解：对于，若，则，满足；若，则，满足；故函数为偶函数，选项A正确；
对于，取，则，，，故选项B错误；
对于，若，则，满足；若，则，满足；故选项C正确；
对于，要为等腰直角三角形，只可能是如下四种情况：
直角顶点在上，斜边在轴上，此时点，点的横坐标为无理数，则中点的横坐标仍然为无理数，那么点的横坐标也为无理数，这与点的纵坐标为矛盾，故不成立；

直角顶点在上，斜边不在轴上，此时点的横坐标为无理数，则点的横坐标也应为无理数，这与点的纵坐标为矛盾，故不成立；

直角顶点在轴上，斜边在上，此时点，点的横坐标为有理数，则中点的横坐标仍然为有理数，那么点的横坐标也应为有理数，这与点的纵坐标为矛盾，故不成立；

直角顶点在轴上，斜边不在上，此时点的横坐标为无理数，则点的横坐标也应为无理数，这与点的纵坐标为矛盾，故不成立．

综上，不存在三个点，，，使得为等腰直角三角形，故选项D正确．
故选：．

13.【答案】， 

【解析】

解：命题是全称量词命题，则全称量词命题的否定是存在量词命题．
即：，，
故答案为：，，

14.【答案】 

【解析】解：幂函数在上单调递增，
所以，
解得．
故答案为：．
15.【答案】 

【解析】解：若函数是奇函数，且在定义域上是减函数，，
可得，
则不等式即为，
可得，
解得，
故答案为：．
16.【答案】 

【解析】解：因为，且，有，所以在上单调递增，
所以，解得，
所以实数的取值范围是
故答案为：
17.【答案】解：由已知可得集合，
当时，集合，则或，
所以或；
因为，则，
即或或，
所以，解得，即实数的范围为． 

18.【答案】解：Ⅰ函数，且此函数图象过点，
，；Ⅱ，，函数是奇函数；
 Ⅲ，，，函数是单调递减函数． 

19.【答案】解：当时，，
，，
函数是定义在上的奇函数，
．
当时，，
，
函数是定义在上的奇函数，
，
，
则．
由可得，的图象，如图所示：

由图象可知，的单调递增区间为，． 

20.【答案】解：函数为偶函数，
，即，
即，得．
当时，，则函数在为增函数，
当时，若函数的值域为，
则，
即，得，

，
则，． 

21.【答案】解：由题意知，当时，，所以．
当时，；
当时，，
所以．
当时，，
所以当时，有最大值，最大值为；
当时，，
当且仅当，即时，有最大值，最大值为，
因为，
所以当年产量为千台时，该企业的年利润最大，最大年利润为万元． 

22.【答案】解：因为，
所以，
所以，
令，则，
因为函数在上是增函数，
在上是增函数，
所以在上为增函数，
所以，
所以的最小值为．
因为二次函数开口向上，对称轴为，
又对任意的，，都有恒成立，
所以对任意的，，都有恒成立，
当，即时，
，
，
所以，
解得，
当，即时，
，
，
当，即时，
，
所以，
解得，
所以的取值范围为，
当，即时，，
所以，
解得舍去，
综上所述，实数的取值范围为