2022-2023学年湖北省随州市中考数学专项突破仿真模拟试题（3月4月）含解析

这是一份2022-2023学年湖北省随州市中考数学专项突破仿真模拟试题（3月4月）含解析
2022-2023学年湖北省随州市中考数学专项突破仿真模拟试题
（3月）　
一、选一选( 每小题3 分,共30分)
1. 方程x2＝4x的解是（　　）
A. x＝0 B. x1＝4，x2＝0 C. x＝4 D. x＝2
2. 用配方法解方程时，原方程应变形为（ ）
A. B. C. D.
3. 若＝，则下列各式没有成立的是（ ）
A. ＝ B. ＝ C. ＝ D. ＝
4. 如图，已知DE∥BC，EF∥AB，则下列比例式错误的是( )

A. B. C. D.
5. 用卡片进行有理数加法训练，李明手中的三张卡片分别是3、-1、-2，刘华手中的三张卡片分别是2、0、-1，如果每人随机抽取一张卡片，则和为正数的概率是( )
A. B. C. D.
6. 如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为(　　)

A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
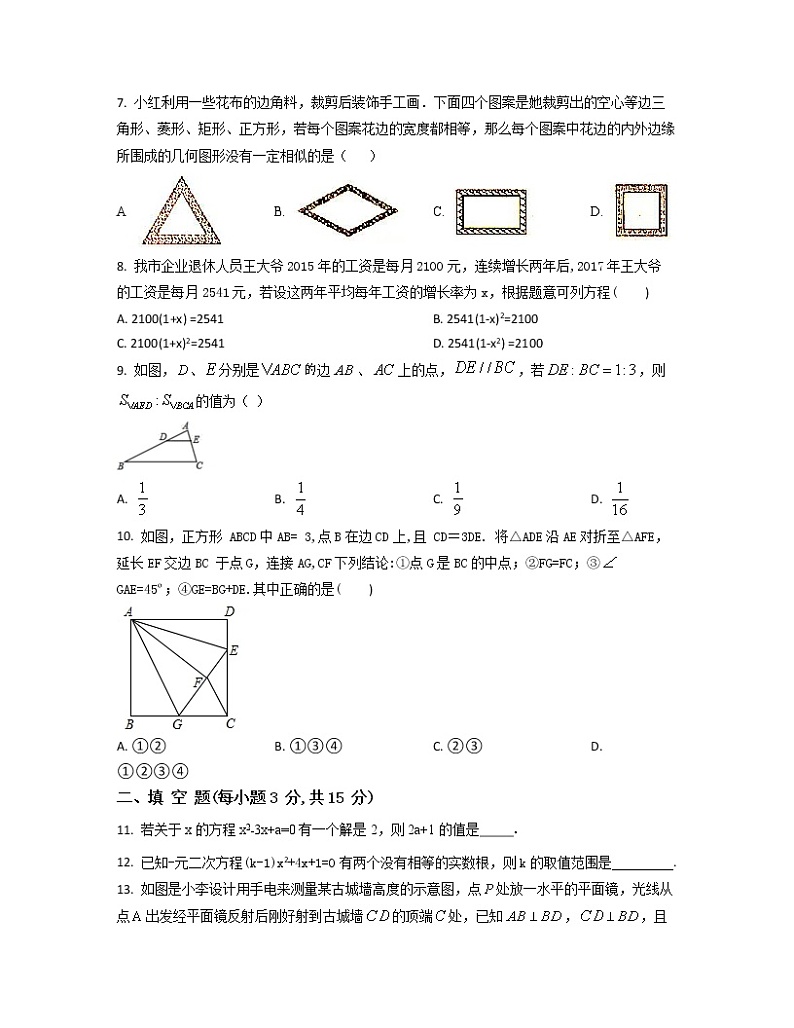
7. 小红利用一些花布的边角料，裁剪后装饰手工画．下面四个图案是她裁剪出的空心等边三角形、菱形、矩形、正方形，若每个图案花边的宽度都相等，那么每个图案中花边的内外边缘所围成的几何图形没有一定相似的是（ ）
A B. C. D.
8. 我市企业退休人员王大爷2015年的工资是每月2100元，连续增长两年后,2017年王大爷
的工资是每月2541元，若设这两年平均每年工资的增长率为x，根据题意可列方程( )
A. 2100(1+x) =2541 B. 2541(1-x)2=2100
C. 2100(1+x)2=2541 D. 2541(1-x2) =2100
9. 如图，、分别是边、上的点，，若，则的值为（ ）

A. B. C. D.
10. 如图，正方形 ABCD中AB= 3,点B在边CD上,且 CD＝3DE. 将△ADE沿AE对折至△AFE，延长EF交边BC 于点G，连接AG,CF下列结论:①点G是BC的中点；②FG=FC；③GAE=45º；④GE=BG+DE.其中正确的是( )

A. ①② B. ①③④ C. ②③ D. ①②③④
二、填 空 题(每小题3 分,共15 分)
11. 若关于x的方程x2﹣3x+a=0有一个解是2，则2а+1的值是_____．
12. 已知-元二次方程(k-1)x2+4x+1=0有两个没有相等的实数根，则k的取值范围是_________.
13. 如图是小李设计用手电来测量某古城墙高度的示意图，点处放一水平的平面镜，光线从点出发经平面镜反射后刚好射到古城墙的顶端处，已知⊥，⊥，且测得=1.1米，=1.9米，=19米， 那么该古城墙的高度是_______米

14. 一个没有透明的口袋里装有若干除颜色外其他完全相同的小球,其中有6个黄球,将口袋中的球摇匀,从中任意摸出一个球记下颜色后再放回,通过大量重复上述试验后发现,摸到黄球的频率稳定在30%,由此估计口袋中共有小球____________个.
15. 如图5, 在△ABC中，AB=8，AC=5，M是AC边上的一点，AM=2， 在AB边上取一点N，使以A、M、N为顶点的三角形与△ABC相似，则AN的长为__________．

三、解 答 题(本大题8 个小题，满分75分)
16. 解方程:(x-3)2-2(3-x) =0
17. 如图，在梯形ABCD中，AD∥BC，∠BAD=90°，对角线BD⊥DC．

（1）△ABD与△DCB相似吗？请回答并说明理由；
（2）如果AD=4，BC=9，求BD的长．
18. 一个没有透明的布袋里装有三个球，其中2个红球，1个白球，它们除颜色没有同外其余都相同：
（1）摸出一个球记下颜色后放回，并搅匀，再摸出一个球，求两次摸出的球恰好颜色没有同的概率（要求画树状图或列表）；
（2）现再将n个白球放入布袋中搅匀后使摸出一个球是白球概率为，求n的值.
19. 如图，在▱ABCD中，∠ABD平分线BE交AD于点E，∠CDB的平分线DF交BC于点F．
（1）求证：△ABE≌△CDF；
（2）若AB=DB，猜想：四边形DFBE是什么四边形？并说明理由．

20. 如图，在方格纸中.

（1）请在方格纸上建立平面直角坐标系，使，，并求出点坐标；
（2）以原点为位似，相似比为2，在象限内将放大，画出放大后的图形；
（3）计算的面积.
21. 宁波桌童装专卖店在中发现，一款童装每件进价为80元，价为120元时，每天可售出20件，为了迎接“五一”国际劳动节，商店决定采取适当的降价措施，以扩大量，增加利润，经市场发现，若每件童装降价，2元，则平均可多售出4件．设每件童裴降价x元；
（1）每天可___件，每件盈利___元；（用含x的代数式表示）
（2）求每件童装降价多少元时，平均每天可赢利1200元．
（3）若店长希望平均每天能赢利2000元，这个愿望能实现吗？请说明理由．
22. 在△ABC中，D是BC的中点，且AD＝AC，DE⊥BC，与AB相交于点E，EC与AD相交于点F．过C点作CG∥AD，交BA的延长线于G，过A作BC的平行线交CG于H点．
（1）若∠BAC＝900，求证：四边形ADCH是菱形；
（2）求证：△ABC∽△FCD；
（3）若DE＝3，BC＝8，求△FCD的面积．

23. 如图，在Rt△ABC中，∠B=90°，BC=5，∠C=30°.点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动，同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动，当其中一个点到达终点时，另一个点也随之停止运动.设点D、E运动的时间是t秒（t＞0）.过点D作DF⊥BC于点F，连接DE、EF.
（1）求证：AE=DF；
（2）四边形AEFD能够成为菱形吗？如果能，求出相应的t值；如果没有能，说明理由.
（3）当t为何值时，△DEF为直角三角形？请说明理由.
















2022-2023学年湖北省随州市中考数学专项突破仿真模拟试题
（3月）　
一、选一选( 每小题3 分,共30分)
1. 方程x2＝4x的解是（　　）
A. x＝0 B. x1＝4，x2＝0 C. x＝4 D. x＝2
【正确答案】B

【分析】移项后分解因式，即可得出两个一元方程，求出方程的解即可．
【详解】解：x2＝4x，
∴x2﹣4x＝0，
则x（x﹣4）＝0，
所以x﹣4＝0，x＝0，
解得x1＝4，x2＝0，
故选B．
本题考查了解一元二次方程，能把一元二次方程转化成一元方程是解此题的关键．
2. 用配方法解方程时，原方程应变形为（ ）
A. B. C. D.
【正确答案】B

【分析】根据配方法解一元二次方程的步骤首先把常数项移到右边，方程两边同时加上项系数一半的平方配成完全平方公式．
【详解】解：
移项得：
方程两边同时加上项系数一半的平方得：
配方得：．
故选：B．
此题考查了配方法解一元二次方程的步骤，解题的关键是熟练掌握配方法解一元二次方程的步骤．配方法的步骤：配方法的一般步骤为：（1）把常数项移到等号的右边；（2）把二次项的系数化为1；（3）等式两边同时加上项系数一半的平方．
3. 若＝，则下列各式没有成立的是（ ）
A. ＝ B. ＝ C. ＝ D. ＝
【正确答案】D

【分析】根据比例设x＝2k，y＝3k，然后代入比例式对各选项分析判断利用排除法求解．
【详解】解：∵，
∴设x＝2k，y＝3k，
A．，正确，故本选项错误；
B．，正确，故本选项错误；
C．，正确，故本选项错误；
D．，故本选项正确．
故选D．
本题考查了比例的性质，利用“设k法”表示出x、y求解更加简便．
4. 如图，已知DE∥BC，EF∥AB，则下列比例式错误的是( )

A. B. C. D.
【正确答案】C

【详解】解：A．∵DE∥BC，
所以A选项的比例式正确；
B．
即所以B选项的比例式正确；
C．
所以C选项的比例式错误；
D．
即所以D选项的比例式错误．
故选C．
5. 用卡片进行有理数加法训练，李明手中的三张卡片分别是3、-1、-2，刘华手中的三张卡片分别是2、0、-1，如果每人随机抽取一张卡片，则和为正数的概率是( )
A. B. C. D.
【正确答案】D

【详解】试题解析：共有9种可能性，满足条件的为：3+2,3+0,3+(−1),−1+2四种,因此概率为
故选D.
6. 如图，已知菱形的两条对角线分别为6cm和8cm，则这个菱形的高DE为(　　)

A. 2.4cm B. 4.8cm C. 5cm D. 9.6cm
【正确答案】B

【详解】解：如图所示：

∵四边形ABCD是菱形，
∴OA=AC=4，OB=BD=3，AC⊥BD，
∴AB=，
∵菱形ABCD的面积=AB•DE=AC•BD=×8×6=24，
∴DE==4.8cm；
故选B．
7. 小红利用一些花布的边角料，裁剪后装饰手工画．下面四个图案是她裁剪出的空心等边三角形、菱形、矩形、正方形，若每个图案花边的宽度都相等，那么每个图案中花边的内外边缘所围成的几何图形没有一定相似的是（ ）
A. B. C. D.
【正确答案】C

【分析】根据相似图形的定义，图形，对选项一一分析，排除没有符合要求答案．
【详解】解：A、形状相同，符合相似形的定义，对应角相等，所以三角形相似，故A选项没有符合要求；
B、形状相同，符合相似形的定义，故B选项没有符合要求；
C、两个矩形，虽然四个角对应相等，但对应边没有成比例，故C选项符合要求；
D、形状相同，符合相似形的定义，故D选项没有符合要求；
故选：C．
本题考查的是相似形的定义，联系图形，即形状相同，大小没有一定相同的图形叫做相似形．全等形是相似形的一个特例．
8. 我市企业退休人员王大爷2015年的工资是每月2100元，连续增长两年后,2017年王大爷
的工资是每月2541元，若设这两年平均每年工资的增长率为x，根据题意可列方程( )
A. 2100(1+x) =2541 B. 2541(1-x)2=2100
C 2100(1+x)2=2541 D. 2541(1-x2) =2100
【正确答案】C

【详解】试题解析：设这两年平均增长率为x，根据题意得：

故选C.
9. 如图，、分别是的边、上的点，，若，则的值为（ ）

A. B. C. D.
【正确答案】C

【分析】根据相似三角形的判定和性质即可得到结论．
【详解】解：∵DE∥BC，
∴△ADE∽△ABC，

故选C．
本题考查了相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．
10. 如图，正方形 ABCD中AB= 3,点B在边CD上,且 CD＝3DE. 将△ADE沿AE对折至△AFE，延长EF交边BC 于点G，连接AG,CF下列结论:①点G是BC的中点；②FG=FC；③GAE=45º；④GE=BG+DE.其中正确的是( )

A. ①② B. ①③④ C. ②③ D. ①②③④
【正确答案】B

【详解】试题解析：①如图1，∵四边形ABCD是正方形，

∴CD=AB=3，
∵CD=3DE，
∴DE=1，
∴CE=2，
由折叠得：DE=EF=1，AD=AF=3，
∴AB=AF，


∴BG=FG，
设BG=x，则CG=3−x，FG=x，
由勾股定理得：


解得：


∴点G是BC的中点；
所以①正确；
②如图2，过F作FH⊥BC于H，






由①得
∴FG≠FC，
所以②没有正确；
③如图1，∵∠DAE=∠FAE，∠BAG=∠FAG，
∴∠BAG+∠DAE=∠FAG+∠FAE，


所以③正确；
④

所以④正确.
故选B.
二、填 空 题(每小题3 分,共15 分)
11. 若关于x的方程x2﹣3x+a=0有一个解是2，则2а+1的值是_____．
【正确答案】5

【分析】将方程的根代入原方程，求出a的值，进一步得到代数式的值．
【详解】关于的方程有一个解是2，
则


12. 已知-元二次方程(k-1)x2+4x+1=0有两个没有相等的实数根，则k的取值范围是_________.
【正确答案】k