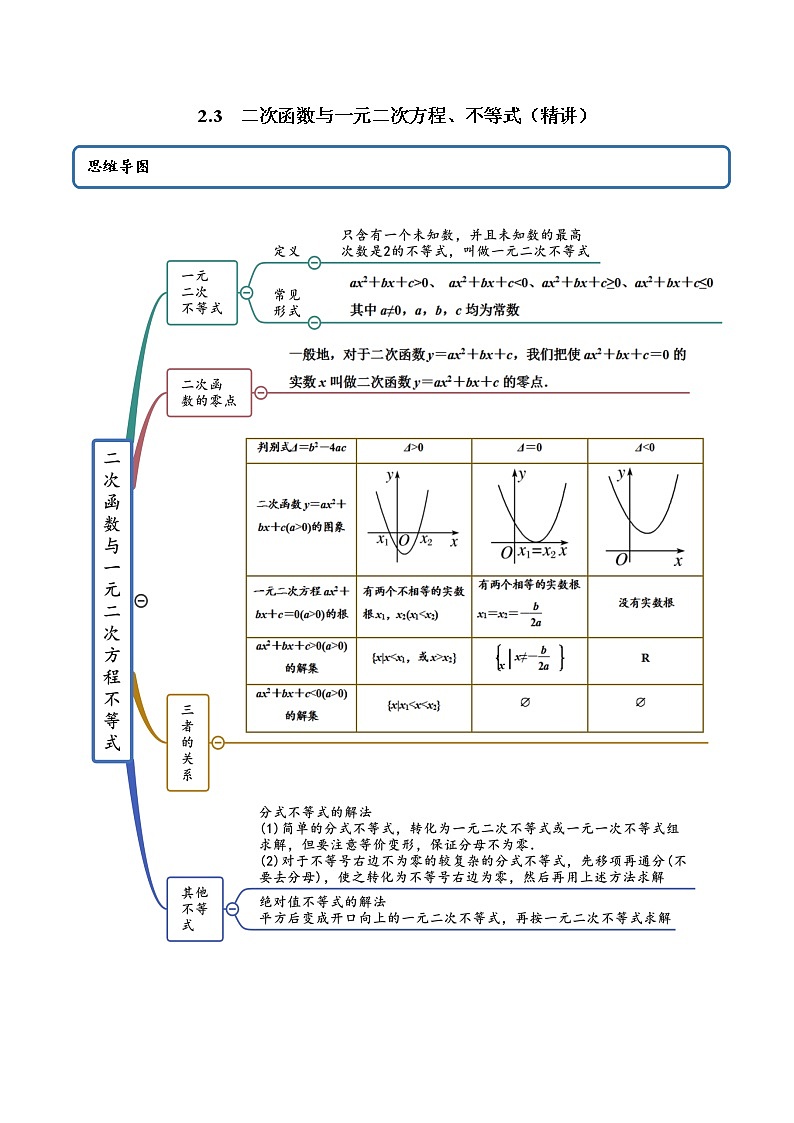
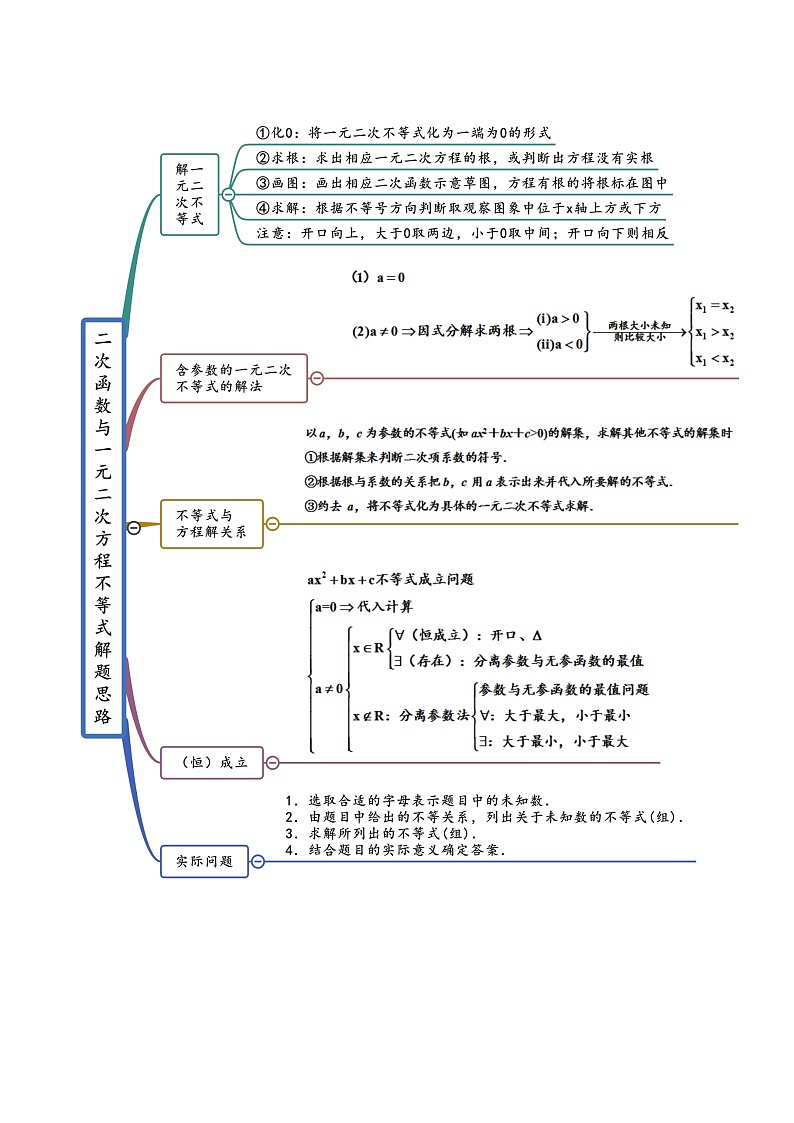
数学必修 第一册2.3 二次函数与一元二次方程、不等式学案

这是一份数学必修 第一册2.3 二次函数与一元二次方程、不等式学案，共16页。学案主要包含了解一元二次不等式，根据一元二次不等式解求参，含参数的一元二次不等式的解法，一元二次不等式恒成立等内容，欢迎下载使用。
2.3  二次函数与一元二次方程、不等式（精讲）    考点一 解一元二次不等式【例1】（2021·利辛县阚疃金石中学）解下列不等式：（1）；（2）.（3）（3）（4）（5）【答案】（1）；（2）.（3）；（4）（5）.【解析】（1）由可得，解原不等式可得.因此，不等式的解集为；（2）由可得，变形得，解原不等式可得或.因此，不等式的解集为.(3)化为，，即，或，原不等式的解集为．（4）由得，即，解得：或，所以不等式的解集是，（5）化为，即，，且，即(且)原不等式的解集为．【一隅三反】1．（2021·安徽亳州市）不等式的解集为（    ）A． B． C． D．【答案】B【解析】由可得，解得，所以不等式的解集为.故选：B2．（2021·全国高一课时练习）求下列不等式的解集.（1）；        （2）；（3）；        （4）；（5）；        （6）．【答案】（1）；（2）；（3）；（4）；（5）；（6）R..【解析】（1）同解于：或，解得：或，所以原不等式的解集为.（2）可化为即或，解得：或无解所以原不等式的解集为.（3）可化为：，解得：，所以原不等式的解集为.（4）可化为：，所以，无解.所以原不等式的解集为.（5）可化为： ，即或，解得：或所以原不等式的解集为.（6）．可化为：，所以,所以原不等式的解集为R.考点二 根据一元二次不等式解求参【例2】（1）（2021·江苏）已知不等式ax2﹣bx+2＞0的解集为{x|＜x＜2}，则不等式2x2+bx+a＜0的解集为（　　）A．{x|＜x＜1} B．{ x|x＜或x＞}C．{x|＜x＜} D．{x|x＜或x＞1}（2）（2021·重庆市育才中学高一月考）关于的方程有两个正的实数根，则实数的取值范围是（    ）.A． B．C． D．（3）（2021·重庆市万州南京中学高一开学考试）如果方程的两个实根一个小于1，另一个大于1，那么实数的取值范围是A． B． C． D．【答案】（1）A（2）D（3）C【解析】（1）不等式ax2﹣bx+2＞0的解集为{x|＜x＜2}，所以，2是方程ax2-bx+2＝0的两个实数根，且a＜0，由根与系数的关系知，解得；所以不等式2x2+bx+a＜0化为2x2﹣x﹣1＜0，解得＜x＜1；所以不等式2x2+bx+a＜0的解集为{x|＜x＜1}．故选：A．（2）方程有两个实数根，△，，的方程有两个正的实数根，对应的二次函数的开口向上，对称轴所以，可得，或，，故选：．（3）因为方程的两个实根一个小于1，另一个大于1，所以可作出函数的简图如下：由图可得：，即：解得： 故选C  【一隅三反】1．（2021·合肥一六八中学高一期末）关于的不等式的解集为，则不等式的解集为（    ）A． B． C． D．【答案】D【解析】的解集是，，得，则不等式，即，解得：，所以不等式的解集是.故选：D2．（2021·广东湛江市·高一期末）已知不等式的解集为，则不等式的解集是（    ）A． B．C．或  D．或【答案】A【解析】的解集为,则的根为，即，，解得，则不等式可化为，即为，解得或，故选：A.3．（2021·江苏）（多选）关于x的不等式的解集为，则下列正确的是（    ）A．B．关于x的不等式的解集为C．D．关于x的不等式的解集为【答案】ACD【解析】A．由已知可得且是方程的两根，A正确，B．由根与系数的关系可得：，解得，则不等式可化为：，即，所以，B错误，C．因为，C正确，D．不等式可化为：，即，解得或，D正确，故选：ACD．4．（2021·上海高一）已知方程有两个负根，求的取值范围．【答案】【解析】设方程两个负根分别为：， 因此有：且且，解得：，所以的取值范围是.5．（2021·上海市杨浦高级中学高一期末）若方程的三个根可以作为一个三角形的三条边的长，则实数的取值范围是______________.【答案】【解析】方程有三根，，有根，方程的，得．又原方程有三根，且为三角形的三边和长．有，，而已成立；当时，两边平方得：．即：．解得．．故答案为：6．（2021·全国高二单元测试）已知方程,求使方程有两个大于的实数根的充要条件．【答案】【解析】令，方程有两个大于的实数根，解得所以，方程,求使方程有两个大于的实数根的充要条件为 考法三 含参数的一元二次不等式的解法【例3】（2021·广东）解关于x的不等式ax2－(a＋1)x＋1<0(a∈R)．【答案】答案见解析【解析】若a＝0，原不等式等价于－x＋1<0，解得x>1．若a<0，原不等式等价于，解得或x>1．若a>0，原不等式等价于．①当a＝1时，，无解； ②当a>1时，，解，得；③当0<a<1时， ，解，得；综上所述，当a<0时，解集为或；   当a＝0时，解集为{x|x>1}；当0<a<1时，解集为； 当a＝1时，解集为∅；当a>1时，解集为．【一隅三反】1．（2021·六安市裕安区新安中学高一期末）已知，关于x的不等式的解集为（    ）A．或 B． C．或 D．【答案】A【解析】不等式化为，，，故不等式的解集为或.故选：A.2．（2021·全国高一）解关于的不等式.【答案】答案见解析.【解析】不等式，化为，当时，解得或，当时，解得R,当时，解得或，综上：当时，不等式的解集是或；当时，不等式的解集是R；当时，不等式的解集是或；3．（2021·安徽省临泉第一中学）解关于的不等式.【答案】答案见解析【解析】由题意可知，可化为（1）当时，不等式化为，解得，（2）当时，不等式化为，解得，（3）当时，不等式化为，解得或，（4）当时，不等式化为，解得，（5）当时，不等式化为，解得或，综上所述，时，不等式的解集为时，不等式的解集为；时，不等式的解集为；时，不等式的解集为；时，不等式的解集为;4．（2021·全国高一课时练习）解关于x的不等式ax2－2(a＋1)x＋4>0.【答案】答案见解析.【解析】(1)当a＝0时，原不等式可化为－2x＋4>0，解得x<2，所以原不等式的解集为{x|x<2}．(2)当a>0时，原不等式可化为(ax－2)(x－2)>0，对应方程的两个根为x1＝，x2＝2.①当0<a<1时，>2，所以原不等式的解集为或；②当a＝1时，＝2，所以原不等式的解集为{x|x≠2}；③当a>1时，<2，所以原不等式的解集为或.(3)当a<0时，原不等式可化为(－ax＋2)(x－2)<0，对应方程的两个根为x1＝，x2＝2，则<2，所以原不等式的解集为.综上，a<0时，原不等式的解集为；a＝0时，原不等式的解集为{x|x<2}；0<a≤1时，原不等式的解集为或；当a>1时，原不等式的解集为或. 考法四 一元二次不等式恒成立【例4】（1）（2021·陵川县高级实验中学校）不等式对一切实数都成立，则实数a的范围是     （2）．（2021·浙江高一期末）若不等式对一切恒成立，则的取值范围是___．（3）．（2021·全国高一）若关于的不等式的解集为，则实数的取值范围是        （4）（2021·北京）若关于的不等式在区间(1，4)内有解，则实数a的取值范围是  【答案】（1）（2）（3）（4）【解析】（1）不等式可变形为由不等式对一切实数都成立，，即，解得故选：C（2）因为不等式对一切恒成立，所以对一切恒成立，令，可知成立，当，函数单调递增，所以，所以.（3）当时，，此不等式无解；当，要使原不等式无解，应满足：，解得：.（4）不等式等价于存在，使成立，即 设 当时， 所以 .【一隅三反】1．（2021·北京高一其他模拟）已知不等式的解集为则的取值范围是        【答案】【解析】因为不等式的解集为所以，解得，所以的取值范围是2．（2021·全国高三专题练习）若关于x的不等式x2－4x≥m对任意x∈(0，1]恒成立，则m的取值范围为________．【答案】m≤－3【解析】只需要在x∈(0，1]时，(x2－4x)min≥m即可．因为函数f(x)＝x2－4x在(0，1]上为减函数，所以当x＝1时，(x2－4x)min＝1－4＝－3，所以m≤－3．3．（2021·江苏扬州市·扬州中学）不等式的解集是空集，则实数的范围为         【答案】【解析】令，解得；当时，不等式化为，解得，不合题意，舍去；当时，不等式化为，无解，符合题意；当，即时，因为的解集是空集，所以恒成立，所以，解得，4．（2021·江西赣州市）若不等式在上有解，则实数的取值范围是      。【答案】【解析】因为不等式在上有解，所以不等式在上有解， 令，则，所以考点五  实际问题【例5】（2021·浙江湖州市·湖州中学高一月考）如图所示，某学校要在长为米，宽为米的一块矩形地面上进行绿化，计划四周种花卉，花卉带的宽度相同，均为米，中间植草坪.为了美观，要求草坪的面积大于矩形土地面积的一半，则的取值范围为________.【答案】【解析】设花卉带宽度为米， 则中间草坪的长为米，宽为米，根据题意可得，整理得：，即，解得或，不合题意，舍去，故所求花卉带宽度的范围为，故答案为：.【一隅三反】1．（2021·浙江高一期末）某小型服装厂生产一种风衣，日销售量x（件）与单价P（元）之间的关系为，生产x件所需成本为C（元），其中元，若要求每天获利不少于1300元，则日销量x的取值范围是A． B． C． D．【答案】B【解析】设该厂每天获得的利润为元，则，，根据题意知，，解得：，所以当时，每天获得的利润不少于元，故选．2．（2020·河北沧州市·高一期中）某种杂志原以每本元的价格销售，可以售出万本.根据市场调查，杂志的单价每提高元，销售量就减少本.设每本杂志的定价为元，要使得提价后的销售总收入不低于万元，则应满足（    ）A． B． C． D．【答案】A【解析】设提价后杂志的定价设为元，则提价后的销售量为：万本，因为销售的总收入不低于万元，列不等式为：，即，即，故选：A.3．（2020·吉林长春市·长春十一高高一期中）某地每年销售木材约20万立方米，每立方米价格为2400元，为了减少木材消耗，决定按销售收入的征收木材税，这样每年的木材销售量减少万立方米，为了既减少木材消耗又保证税金收入每年不少于900万元，则的取值范围是（    ）A． B．C． D．【答案】B【解析】由题意可得，，整理可得解得故选：B4．（2021·浙江）商场若将进货单价为8元的商品按每件10元出售．每天可销售100件，现准备采用提高售价来增加利润．已知这种商品每件销售价提高1元，销售量就要减少10件．那么要保证每天所赚的利润在320元以上，销售价每件可定为（    ）A．11元 B．16元C．12元到16元之间 D．13元到15元之间【答案】C【解析】设销售价定为每件元,利润为元，则，由题意可得：，即， 所以，解得：，所以每件销售价应定为12元到16元之间，故选：C.