数学必修 第一册4.1 指数学案

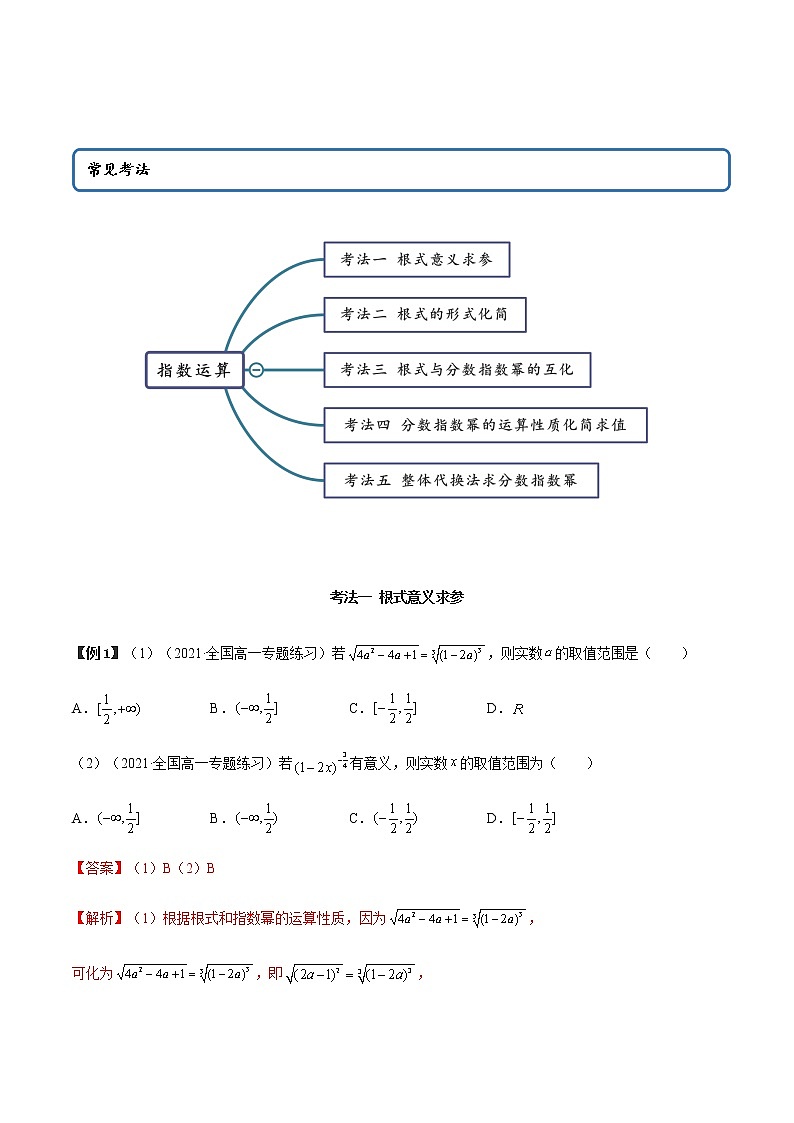
这是一份数学必修 第一册4.1 指数学案，共14页。学案主要包含了根式意义求参，根式的形式化简，根式与分数指数幂的互化，分数指数幂的运算性质化简求值，整体代换法求分数指数幂等内容，欢迎下载使用。
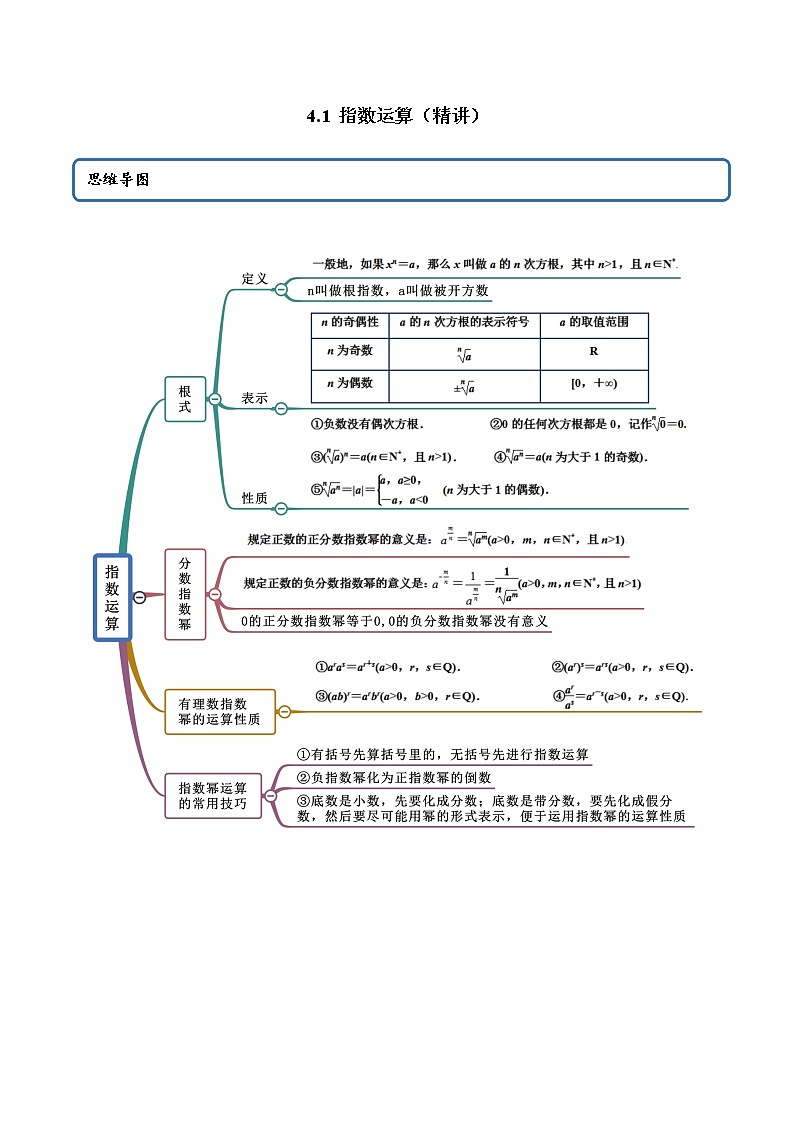
4.1 指数运算（精讲）      考法一 根式意义求参 【例1】（1）（2021·全国高一专题练习）若，则实数的取值范围是（    ）A． B． C． D．（2）（2021·全国高一专题练习）若有意义，则实数的取值范围为（    ）A． B． C． D．【答案】（1）B（2）B【解析】（1）根据根式和指数幂的运算性质，因为，可化为，即，可得，所以，即．故选：B.（2）由，要使得有意义，则满足，解得，即实数的取值范围为．故选：B．  【一隅三反】1．（2021·全国高一课时练习）若xn＝a（x≠0），则下列说法中正确的个数是（    ）①当n为奇数时，x的n次方根为a；②当n为奇数时，a的n次方根为x；③当n为偶数时，x的n次方根为±a；④当n为偶数时，a的n次方根为±x.A．1 B．2C．3 D．4【答案】B【解析】n为奇数时，a的n次方根只有1个，为x；当n为偶数时，由于（±x）n＝xn＝a，所以a的n次方根有2个，为±x.所以说法②④是正确的，故选：B.2．（2021·上海高一专题练习）在①，②，③，④中，n∈N*，a∈R时各式子有意义的是（    ）A．①② B．①③ C．②③④ D．①②④【答案】B【解析】由>0知①有意义；由<0知②无意义；③中开奇数次方根，所以有意义；当a<0时，a5<0，此时④无意义.故选:B.考点二 根式的形式化简 【例2】（1）（2021·上海高一专题练习）若，则化简的结果是（    ）A． B． C． D．（2）（2021·全国高一课时练习）若代数式有意义，则（    ）A． B． C． D．（3）（2020·上海）化简：①；②）【答案】（1）B（2）B（3）①；②）.【解析】（1）因为，所以，所以.故选:B.（2）由有意义，得解得．所以所以．故选：B．（3）①原式 .②原式，即【一隅三反】1．（2021·全国）若，则等于（    ）A． B． C． D．非以上答案【答案】B【解析】因为，所以，原式.故选:B.2．（2021·上海闵行）当时，=___________.【答案】【解析】由，则，故答案为：3．（2021·全国高一课时练习）化简－（－3<x<3）.【答案】.【解析】原式，∵－3<x<3，∴－4<x－1<2，0<x＋3<6.当－4<x－1<0，即－3<x<1时，|x－1|－|x＋3|＝1－x－（x＋3）＝－2x－2；当0≤x－1<2，即1≤x<3时，|x－1|－|x＋3|＝x－1－（x＋3）＝－4.∴－＝.考法三 根式与分数指数幂的互化【例3】（2021·上海高一专题练习）将下列根式化成有理数指数幂的形式：（1）（a>0）；（2）（x>0）；（3）（b>0）.【答案】（1）；（2）；（3）.【解析】（1）原式====.（2）原式======.（3）原式===.【一隅三反】1．（2021·全国高一课时练习）下列关系式中，根式与分数指数幂的互化正确的是（    ）A．－＝（－x）（x＞0）B．＝y（y＜0）C．xy＝ （x＞0，y＞0）D．x＝－ （x≠0）【答案】C【解析】对于A，－＝－x，故A错误；对于B，当y＜0时，＞0，y＜0，故B错误；对于C，xy＝ （x＞0，y＞0），故C正确；对于D，x＝ （x≠0），故D错误.故选：C2．（2021·上海高一专题练习）用有理数指数幂的形式表示下列各式（a>0，b>0）.（1）；（2）；（3）；（4）；（5）；（6）.【答案】（1）；（2）；（3）；（4）；（5）；（6）.【解析】（1）原式=.（2）原式=.（3）原式=.（4）原式=.（5）原式=.（6）原式====.   考点四 分数指数幂的运算性质化简求值【例4】（2021·全国高一课时练习）计算或化简：（1）－10＋；（2）·.【答案】（1）－；（2）【解析】（1）原式;（2）原式.【一隅三反】1．（2021·全国高一课时练习）下列式子中，错误的是（    ）A．B．C．D．【答案】C【解析】对于A，原式，A正确；对于B，原式，B正确；对于C，原式, C错误；对于D，原式，D正确.故选：C.2．（2021·上海高一专题练习）计算下列各式：（1）；（2）；（3）；（4）；（5）【答案】(1)；(2)100；(3)3；(4)；(5).【解析】(1)原式.(2)原式.(3)原式.(4)原式.(5)原式.考点五 整体代换法求分数指数幂【例5】（2021·全国）已知，求下列各式的值．（1）；（2）； （3）．【答案】（1） ；（2） ；（3） ．【解析】（1）∵，∴；（2）∵，∴；（3）∵，，∴ ∴.【一隅三反】1．（2021·全国高一课时练习）若，则___________.【答案】6【解析】因为，所以，即，所以，所以.故答案为：6.2．（2021·全国）若，则________．【答案】【解析】，所以，所以．故答案为：．3．（2021·全国高一课时练习）已知，其中，求的值．【答案】1【解析】由可知，所以==1.4．（2021·江西高安中学高一月考）计算：（1）；（2）已知：，求的值．【答案】（1）；（2）．【解析】（1），.（2）由，平方得，即，平方得，即，所以原式=．