高中4.4 对数函数学案

4.4 对数函数

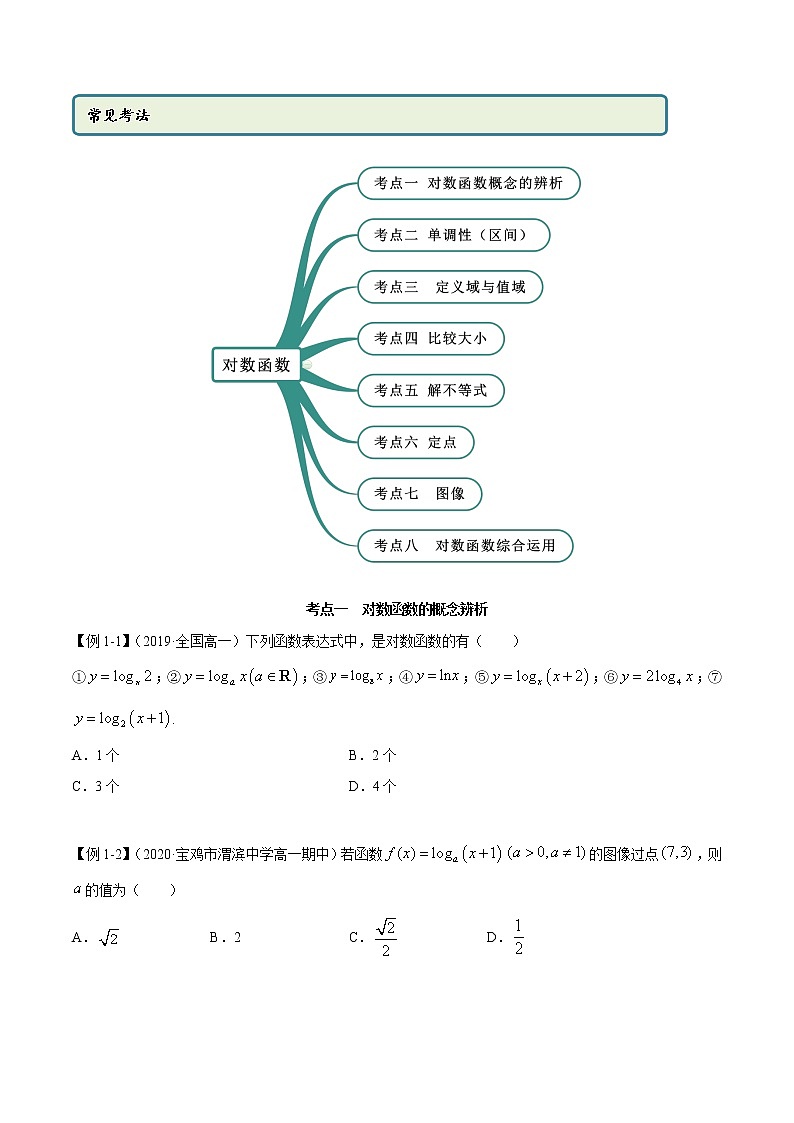
考点一  对数函数的概念辨析

【例1-1】（2019·全国高一）下列函数表达式中，是对数函数的有（    ）

①；②；③；④；⑤；⑥；⑦.

A．1个 B．2个

C．3个 D．4个

【例1-2】（2020·宝鸡市渭滨中学高一期中）若函数的图像过点，则的值为（    ）

A． B．2 C． D．

【一隅三反】

1．（2020·全国高一课时练习）下列函数为对数函数的是（    ）

A．y＝logax＋1(a＞0且a≠1)           B．y＝loga(2x)(a＞0且a≠1)

C．y＝log(a－1)x(a＞1且a≠2)             D．y＝2logax(a＞0且a≠1)

2．下列函数是对数函数的是(   )

A． B． 

C． D． 

3．下列函数，是对数函数的是

A．y=lg10x B．y=log3x2

C．y=lnx D．y=log（x–1）

4．（2020·全国高一课时练习）对数函数的图象过点M(16,4)，则此对数函数的解析式为(　　)

A．y＝log4x B．y＝ x

C．y＝ x D．y＝log2x

考点二  单调性（区间）

【例2】（1）（2020·辽宁锦州·高二期末）函数的单调减区间是（    ）

A． B． C． D．

（2）（2019·四川省新津中学高一月考）已知在上是增函数，则实数的取值范围是（    ）

A． B．

C． D．

【一隅三反】

1．（2019·小店·山西大附中高一期中）函数的单调递减区间为（   ）

A． B． C． D．

2．函数y=是

A．区间（–∞，0）上的增函数 B．区间（–∞，0）上的减函数

C．区间（0，+∞）上的增函数 D．区间（0，+∞）上的减函数

3．（2020·全国）已知函数在上单调递增，则的取值范围是（    ）

A． B． C． D．

考点三  定义域和值域

【例3】（1）（2020·永昌县第四中学高二期末（文））函数的定义域为（    ）

A． B． C． D．

（2）（2019·新疆兵团第二师华山中学高二月考（文））函数的值域是（   ）.

A．R B． C． D．

【一隅三反】

1．（2020·沭阳县修远中学高二期末）函数的定义域为（    ）

A． B． C． D．

2．（2020·湖南高新技术产业园区·衡阳市一中高三月考）已知函数的定义域是，则函数的定义域是________.

3．（2019·北）若函数 则函数的值域是（   ）

A． B． C． D．

考点四  比较大小

【例4】（2020·全国高一课时练习）比较下列各组数中两个值的大小．

（1）log23.4，log28.5；

（2）log0.31.8，log0.32.7；

（3）loga5.1，loga5.9(a>0，且a≠1)．

【一隅三反】

1．（2020·辽源市田家炳高级中学校高二期末（文））已知，，，则，，的大小关系是（    ）

A． B． C． D．

2．（2020·哈尔滨市第十二中学校高二期末（文））已知，，，则（    ）

A． B．

C． D．

3．（2020·贵州铜仁伟才学校高二期末（文））若，，，则（    ）

A． B．

C． D．

考点五  解不等式

【例5】（2020·内蒙古集宁一中高二期末（文））不等式的解集是________.

【一隅三反】

1．（2020·安徽马鞍山）已知函数是定义域为的偶函数，在上单调递减，则不等式的解集是（    ）

A． B．（1，3） C． D．

2．（2020·湖北）已知函数是定义在上的奇函数，当时，，若实数满足，则的取值范围是（    ）

A． B． C． D．

3．（2019·山东省实验中学高三月考）已知函数 (>0且≠1)的图像过点(9，2)

(1)求函数的解析式；

(2)解不等式．

考点六  定点

【例6】（2020·山东省枣庄市第十六中学高一期中）函数的图象恒过定点，（其中且），则的坐标为__________.

【一隅三反】

1.（2020·云南省玉溪第一中学高一期中）函数的图象必过定点（　　）

A． B． C． D．

2．（2019·重庆高一月考）函数（，且）的图象恒过点（   ）

A． B． C． D．

考点七  图像

【例7】（2020·哈尔滨市第十二中学校高二期末（文））函数（且）与函数（且）在同一直角坐标系内的图象可能是（    ）

A． B． C． D．

【一隅三反】

1．（2020·山东滨州·高二期末）函数的图象大致是（    ）

A． B．

C． D．

2．（2020·全国高一课时练习）函数y＝2log4(1－x)的图象大致是

A． B． 

C． D．

3.如图，若C1，C2分别为函数y＝logax和y＝logbx的图象，则(　　)

A．0＜a＜b＜1                B．0＜b＜a＜1

C．a＞b＞1                     D．b＞a＞1

考点八  对数函数综合运用

【例8】（2020·甘肃省会宁县第四中学高二期末（文））已知函数．

（1）求的值；

（2）求函数的定义域

（3）判断函数的奇偶性，并证明.

【一隅三反】

1．（2020·湖南桃江·高二期末）已知函数且.

（1）求的定义域；

（2）解关于的不等式.

2．（2020·山东省枣庄市第十六中学高一期中）已知函数，a常数.

（1）若，求证为奇函数，并指出的单调区间；

（2）若对于，不等式恒成立，求实数m的取值范围.