初中数学中考复习 考点06 一元二次方程及其应用（原卷版）

考点六   一元二次方程及其应用

【命题趋势】

  在中考，一元二次方程的概念主要在选择题和填空题中考查，解一元二次方程（包括配方法）常以选择题、填空题和计算题考查，一元二次方程根的判别式常以选择题、填空题考查，一元二次方程应用常在选择题、填空题和解答题的第一问考查。

【中考考查重点】

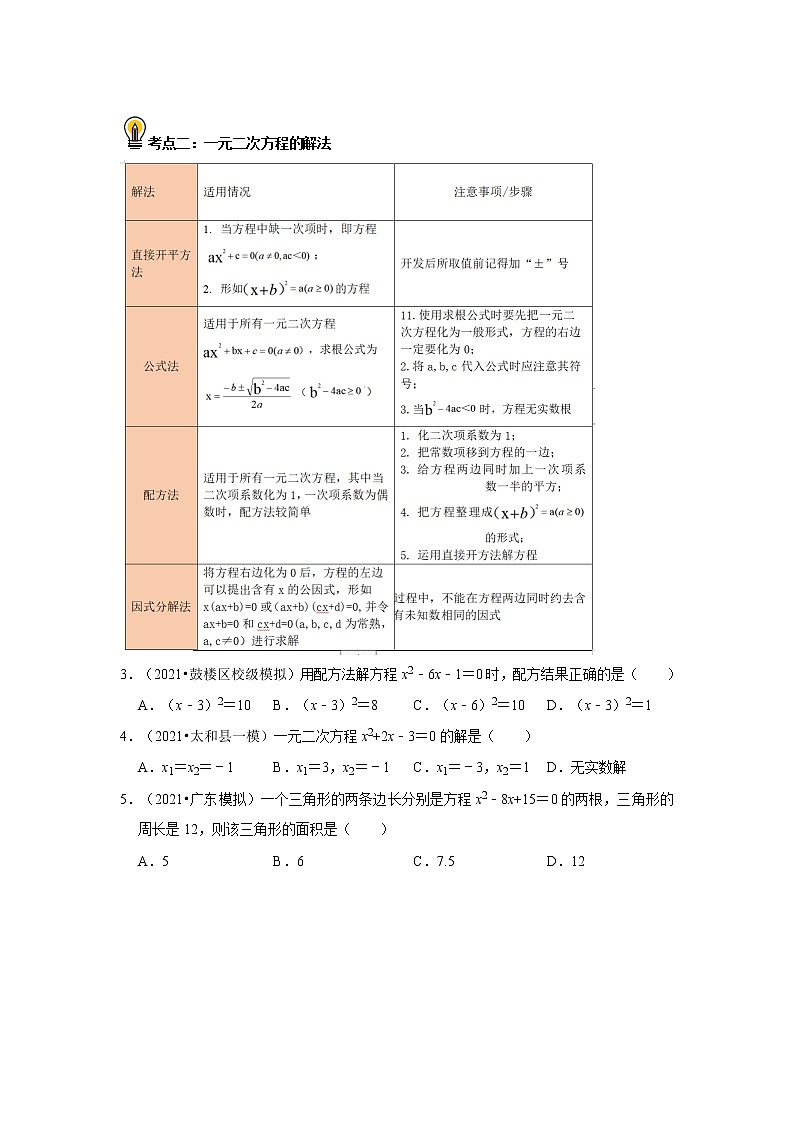
一、掌握配方法，能用配方法、公式法、因式分解法解数字系数的一元二次方程

二、掌握一元二次方程根的判别式判别方程是否由实根和两个实根是否相等

三、熟练掌握一元二次方程的几种类型应用

     考点一：一元二次方程的相关概念及解法

1．（2021秋•农安县期末）下列方程中，是一元二次方程的是（　　）

A．+x﹣1＝0 B．3x+1＝5x+42 C．ax2+bx+c＝0 D．m2﹣2m+1＝0

2．（2019秋•武汉期末）将一元二次方程5x2﹣1＝4x化成一般形式后，二次项的系数和一次项系数分别是（　　）

A．5，﹣1 B．5，4 C．5，﹣4 D．5，1

考点二：一元二次方程的解法

3．（2021•鼓楼区校级模拟）用配方法解方程x2﹣6x﹣1＝0时，配方结果正确的是（　　）

A．（x﹣3）2＝10 B．（x﹣3）2＝8 C．（x﹣6）2＝10 D．（x﹣3）2＝1

4．（2021•太和县一模）一元二次方程x2+2x﹣3＝0的解是（　　）

A．x1＝x2＝﹣1 B．x1＝3，x2＝﹣1 C．x1＝﹣3，x2＝1 D．无实数解

5．（2021•广东模拟）一个三角形的两条边长分别是方程x2﹣8x+15＝0的两根，三角形的周长是12，则该三角形的面积是（　　）

A．5 B．6 C．7.5 D．12

6．（2021•毕节市）已知关于x的一元二次方程ax2﹣4x﹣1＝0有两个不相等的实数根，则a的取值范围是（　　）

A．a≥﹣4 B．a＞﹣4 C．a≥﹣4且a≠0 D．a＞﹣4且a≠0

7．（2021秋•富裕县期末）方程kx2﹣6x+1＝0有实数根，则k的取值范围是（　　）

A．k≤9 B．k≤9且≠0 C．k≠0 D．k＞9

8．（2021•博山区一模）设a，b是方程x2+x﹣2022＝0的两个实数根，则a2+2a+b的值为（　　）

A．2020 B．2021 C．2022 D．2023

9．（2021秋•汝阳县期末）已知关于x的方程x2﹣（m+2）x+（2m﹣1）＝0．

（1）求证：方程恒有两个不相等的实数根．

（2）若此方程的一个根是1，请求出方程的另一个根，并求以此两根为边长的直角三角形的面积．

考点四：一元二次方程的应用

10．（2021秋•铁西区期末）某品牌足球2020年单价为200元，到2022年后，公司将该品牌足球的单价确定为162元，则2020年到2022年该品牌足球单价平均每年降低的百分率是（　　）

A．10% B．19% C．20% D．30%

11．（2021•香坊区二模）某中学初四学生毕业时，每个同学都给其他同学写了一份毕业留言，全班共写了纪念留言1640份，则全班共有学生（　　）名．

A．39 B．40 C．41 D．42

12．（2021秋•射洪市期中）新冠病毒主要是经呼吸道飞沫传播的，在无防护下传播速度很快．已知有1个人患了新冠肺炎，经过两轮传染后共有169个人患了新冠肺炎，每轮传染中平均一个人传染m人，则m的值为（　　）

A．11 B．12 C．13 D．14

13．（2021春•青秀区校级期末）某学校生物兴趣小组在该校空地上围了一块面积为200m2的矩形试验田，用来种植蔬菜．如图，试验田一面靠墙，墙长35m，另外三面用49m长的篱笆围成，其中一边开有一扇1m宽的铁制小门．设试验田垂直于墙的一边AB的长为xm，则AB的长为（　　）

A．20m或5m B．25m或5m C．5m D．20m

1．（2021秋•长春期末）下列方程中，是关于x的一元二次方程的是（　　）

A．x+＝2 B．2x2﹣x＝1 C．3x3＝1 D．xy＝4

2．（2017秋•武清区期中）将一元二次方程3x2+1＝6x化成一般形式后，一次项系数、常数项分别为（　　）

A．1，﹣6 B．﹣6，1 C．1，6 D．6，1

3．（2021•南充一模）方程（9x﹣1）2＝1的解是（　　）

A．x1＝x2＝ B．x1＝x2＝ 

C．x1＝0，x2＝ D．x1＝0，x2＝﹣

4．（2021•庐阳区校级一模）方程（x﹣1）（x+3）＝x﹣1的根是（　　）

A．x＝1 B．x1＝﹣3，x2＝1 C．x1＝﹣2，x2＝1 D．x1＝﹣3，x2＝0

5．（2021秋•新抚区期末）关于x的一元二次方程kx2﹣2x﹣1＝0有两个实数根，则k的取值范围（　　）

A．k≥﹣1 B．k≤﹣1 C．k＞﹣1且k≠0 D．k≥﹣1且k≠0

6．（2021秋•零陵区期末）方程9x2﹣16＝0的根是 　　   ．

7．（2021秋•江油市期末）已知a，b是方程x2﹣3x﹣4＝0的两根，则代数式a+b的值为（　　）

A．3 B．﹣3 C．4 D．﹣4

8．（2021秋•郧西县期末）已知方程x2﹣4x+k＝0的一个根是x1＝﹣1，则方程的另一根x2＝　　．

9．（2021秋•舞钢市期末）若a、b是方程x2+x﹣2021＝0的两根，则a2+2a+b＝　   　．

10．（2021秋•津南区期中）某中学九年级以班级为单位组织篮球比赛，每两班之间都要比赛一场，共比赛了15场，设参赛班级的个数为x，则x的值为（　　）

A．5 B．6 C．7 D．8

11．（2021•黑龙江）有一个人患了流行性感冒，经过两轮传染后共有144人患了流行性感冒，则每轮传染中平均一个人传染的人数是（　　）

A．14 B．11 C．10 D．9

12．（2020•无锡）已知关于x的方程：4x2+4mx+2m﹣1＝0（m为实数）．

（1）求证：对于任意给定的实数m，方程恒有两个实数根；

（2）设x1，x2是方程的两个实数根，求证：x1+x2+m＝0．

1．（2021•赤峰）一元二次方程x2﹣8x﹣2＝0，配方后可变形为（　　）

A．（x﹣4）2＝18 B．（x﹣4）2＝14 C．（x﹣8）2＝64 D．（x﹣4）2＝1

2．（2021•西藏）已知一元二次方程x2﹣10x+24＝0的两个根是菱形的两条对角线长，则这个菱形的面积为（　　）

A．6 B．10 C．12 D．24

3．（2021•河池）关于x的一元二次方程x2+mx﹣m﹣2＝0的根的情况是（　　）

A．有两个不相等的实数根 

B．有两个相等的实数根 

C．没有实数根 

D．实数根的个数由m的值确定

4．（2021•丹东）若实数k、b是一元二次方程（x+3）（x﹣1）＝0的两个根，且k＜b，则一次函数y＝kx+b的图象不经过（　　）

A．第一象限 B．第二象限 C．第三象限 D．第四象限

5．（2021•黔西南州）三角形两边的长分别为2和5，第三边的长是方程x2﹣8x+15＝0的根，则该三角形的周长为 　　．

6．（2021•贵港）已知关于x的一元二次方程x2﹣kx+k﹣3＝0的两个实数根分别为x1，x2，且x12+x22＝5，则k的值是（　　）

A．﹣2 B．2 C．﹣1 D．1

7．（2021•宜宾）若m、n是一元二次方程x2+3x﹣9＝0的两个根，则m2+4m+n的值是（　　）

A．4 B．5 C．6 D．12

8．（2020•济南）如图，在一块长15m、宽10m的矩形空地上，修建两条同样宽的相互垂直的道路，剩余部分栽种花草，要使绿化面积为126m2，则修建的路宽应为 　　米．

9．（2020•黔西南州）有一人患了流感，经过两轮传染后，共有121人患了流感，每轮传染中平均每人传染了 　　个人．

10．（2021•毕节市）某校八年级组织一次篮球赛，各班均组队参赛，赛制为单循环形式（每两班之间都赛一场），共需安排15场比赛，则八年级班级的个数为（　　）

A．5 B．6 C．7 D．8

11．（2021•黄石）已知关于x的一元二次方程x2+2mx+m2+m＝0有实数根．

（1）求m的取值范围；

（2）若该方程的两个实数根分别为x1、x2，且x12+x22＝12，求m的值．

1．（2021•潜江模拟）下列是一元二次方程的是（　　）

A．﹣5x+2＝1 B．2x2﹣y+1＝0 C．x2+2x＝0 D．x2﹣＝0

2．（2021•临沂模拟）用配方法解一元二次方程x2﹣2x﹣2021＝0，则方程可变形为（　　）

A．（x﹣2）2＝2025 B．（x+2）2＝2025 

C．（x﹣1）2＝2022 D．（x+1）2＝2022

3．（2021•深圳模拟）若x1，x2是方程x2＝16的两根，则x1+x2的值是（　　）

A．16 B．8 C．4 D．0

4．（2021•桂林模拟）一元二次方程x2+2x﹣1＝0的根的情况是（　　）

A．没有实数根 B．只有一个实数根 

C．有两个相等的实数根 D．有两个不相等的实数根

5．（2021•江油市二模）若关于x的一元二次方程（1﹣2a）x2﹣2x﹣1＝0有实数根，则a的取值范围是（　　）

A．0≤a≤1 B．0＜a≤1 

C．0≤a≤1且a≠ D．0≤a＜1且a≠

6．（2021•遵义一模）已知关于x的一元二次方程x2﹣3x+1＝0有两个不相等的实数根x1，x2，则x12+x22的值是（　　）

A．﹣7 B．7 C．2 D．﹣2

7．（2021•江西模拟）如图，为美化校园环境，学校打算在长为30m，宽为20m的长方形空地上修建上一个长方形花圃，并将花圃四周余下的空地修建成宽为am的通道．若花圃的面积恰好等于264m2，则通道的宽a＝　　m．

8．（2021•哈尔滨模拟）由于受“一带一路”国家战略策略的影响，某种商品的进口关税连续两次下调，由4000美元下调至2560美元，则平均每次下调的百分率为　　．

9．要组织一次排球邀请赛，参赛的每两个队之间都要比赛一场，根据场地和时间等条件，赛程计划安排7天，每天安排4场比赛，比赛组织者应邀请 　　队参赛．

10．（2021•蜀山区校级模拟）某校九年级3月份中考模拟总分760分以上有300人，同学们在老师们的高效复习指导下，复习效果显著，在4月份中考模拟总分760分以上人数比3月份增长5%，且5，6月份的760分以上的人数按相同的百分率x继续上升，则6月份该校760分以上的学生人数（　　）

A．300（1+5%）（1+2x）人 B．300（1+5%）（1+x）2人 

C．（300+5%）（300+2）人 D．300（1+5%+2x）人

11．（2021•凉山州模拟）已知关于x的一元二次方程x2﹣（2k+4）x+k2+4k+3＝0．

（1）求证：不论k取何值，此一元二次方程总有两个不相等的实数根；

（2）若此一元二次方程的两根是Rt△ABC两直角边AB、AC的长，斜边BC的长为10，求k的值．